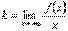Основные сведения о матрицах. Операции над матрицами.

Основные сведения о матрицах. Операции над матрицами.

Матрицей размера m x n называется прямоугольная таблица чисел, содержащая m строк и n столбцов.

Числа, составляющие матрицу, называются элементами матрицы. Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C,….

Для обозначения элементов матрицы используются строчные буквы с двойным индексом, например: a_ij, где i - номер строки, j - номер столбца.

Две матрицы A и B одного размера называются равными, если они совпадают поэлементно, a_ij = b_ij для любых i=1,2,…m; j=1,2,…n, виды матриц. Матрица, состоящая из одной строки, называется матрицей (вектором)- строкой, а из одного столбца - матрицей (вектором)- столбцом: Элементы матрицы a_ij, у которых номер столбца равен номеру строки называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы a₁₁, a₂₂,…,a_nn. Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.

Операции над матрицамиНад матрицами, как и над числами, можно производить ряд операций, причем некоторые из них аналогичны операциями над числами, а некоторые - специфические. 1. Умножение матрицы на число. Произведение матрицы А на число 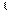называется матрица B= 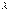A, элементы которой b_ij= 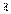a_ij для i=1,2,…m; j=1,2,…n Следствие: Общий множитель всех элементов матрицы можно выносить за знак матрицы.

В частности, произведение матрицы А на число 0 есть нулевая матрица.

2. Сложение матриц. Суммой двух матриц А и В одинакового размера m называется матрица С=А+В, элементы которой c_ij=a_ij+b_ij для i=1,2,…m; j=1,2,…n (т.е. матрицы складываются поэлементно).

3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A-B=A+(-1)∙B.

4. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц A_m 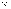∙B _k называется такая матрица C_m 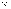, каждый элемент которой cij равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В:

5.Возведение в степень. Целой положительной степенью (m 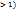квадратной матрицы А называется произведение m матриц, равных А, т.е.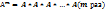

6.Транспонирование матрицы-переход от матрицы А к матрице А’, в которой строки и столбцы поменялись местами с сохранением порядка. Матрица А’ называется транспонированной относительно матрицы А.

Определитель n-го порядка и их свойства.

Определителем (детерминантом) 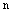– го порядка или определителем

(детерминантом) квадратной матрицы 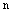– го порядка называют алгебраическую сумму всех членов определителя данной матрицы, взятых со своими знаками.

Ранг матрицы

Ранг матрицы — наивысший из порядков миноров этой матрицы, отличных от нуля. Обычно ранг матрицы A обозначается ( 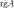) или . 2 метода вычисления ранга матрицы: 1) метод окаймляющих миноров; 2) метод элементарных преобразований. Суть первого метода заключается в следующем. Пусть в матрице A найден ненулевой минор k-го порядка M. Рассмотрим все миноры (k + 1)-го порядка, включающие в себя (окаймляющие) минор M; если все они равны нулю, то ранг матрицы равен k. В противном случае среди окаймляющих миноров найдется ненулевой, и вся процедура повторяется. Что касается второго метода, то воспользуемся элементарными преобразованиями 1) перестановка двух любых строк (или столбцов),2) умножение строки (или столбца) на отличное от нуля число,3) прибавление к одной строке (или столбцу) другой строки (или столбца), умноженной на некоторое число.

5. Система n линейных уравнений с n неизвестными. Правило Крамера.Пустьдана система n линейных уравнений с n неизвестными.

или в матричной форме А*Х=В.

Основная матрица А такой системы квадратная. Определитель этой матрицы

называется определителем системы. Если определитель системы

отличен от нуля, то система называется невырожденной.

Найдем решение данной системы уравнений в случае D¹0

Умножив обе части уравнения А*Х=В слева на матрицу A^-1, получим

A^-1*A*X=A^-1*BПоскольку. A^-1*A=E и Е*Х=Х , то

X=A^-1*B (4.1)

Расширенной матрицей системы называется матрица A системы, дополненная столбцом свободных членов

Отыскание решения системы по формуле (4.1) называют матричным способом решения системы.

Матричное равенство (4.1) запишем в виде 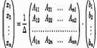то есть Отсюда следует, что Но 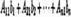есть разложение определителя по элементам первого столбца. Определитель D получается из определителяD путем замены первого столбца коэффициентов столбцом из свободных членов. Итак, 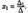Аналогично: 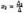, где D 2 получен из D путем замены второго столбца коэффициентов столбцом из свободных членов: ,..., Формулы 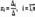называются формулами Крамера.Итак, невырожденная система n линейных уравнений с n неизвестными имеет единственное решение, которое может быть найдено матричным способом, либо по формулам Крамера

Правило Крамера.Если в системе 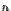линейных уравнений с 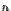неизвестными 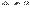, то система имеет решение и притом единственное. Это решение задается формулами

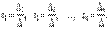
Доказательство. По теореме 14.1 обратная матрица находится по формуле

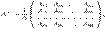
где 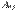-- алгебраические дополнения. Тогда из (15.3) следует, что

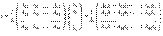Заметим, что по формуле (14.13) разложение определителя 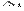по первому столбцу в точности совпадает с первым элементом матрицы-столбца в правой части последнего равенства, разложение определителя 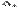по второму столбцу дает второй элемент матрицы-столбца и т.д. Поэтому 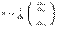, откуда и следует утверждение теоремы.

Первый замечательный предел

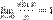
Доказательство

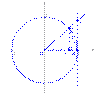Рассмотрим односторонние пределы 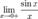и 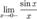и докажем, что они равны 1.

Пусть 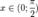. Отложим этот угол на единичной окружности (R = 1).

Точка K — точка пересечения луча с окружностью, а точка L — с касательной к единичной окружности в точке (1;0). Точка H — проекция точки K на ось OX.

Очевидно, что:

(где S_sectOKA — площадь сектора OKA)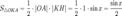

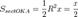
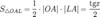(из : | LA | = tgx)

Подставляя в (1), получим: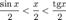

Так как при :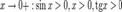

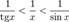Умножаем на sinx: 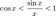Перейдём к пределу: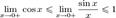

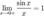
Найдём левый односторонний предел:

Правый и левый односторонний пределы существуют и равны 1, а значит и сам предел равен 1.

Следствия

·

·

·

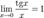
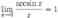
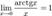
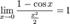· Доказательство следствий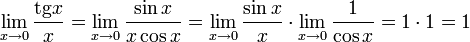

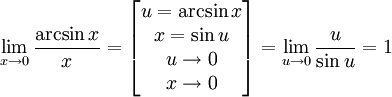
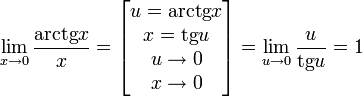
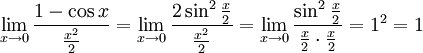
Второй замечательный предел

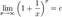Доказательство второго замечательного предела:

Доказательство для натуральных значений x 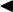Докажем вначале теорему для случая последовательности 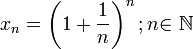По формуле бинома Ньютона: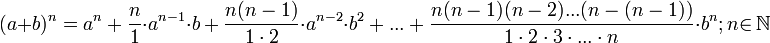

Полагая 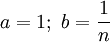, получим:

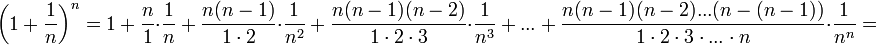
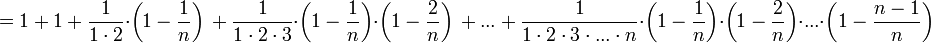(1)

Из данного равенства (1) следует, что с увеличением n число положительных слагаемых в правой части увеличивается. Кроме того, при увеличении n число убывает, поэтому величины 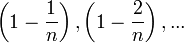возрастают. Поэтому последовательность 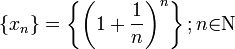— возрастающая, при этом

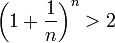(2).

Покажем, что она ограничена. Заменим каждую скобку в правой части равенства на единицу, правая часть увеличится, получим неравенство

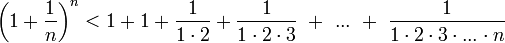
Усилим полученное неравенство, заменим 3,4,5, …, стоящие в знаменателях дробей, числом 2:

.

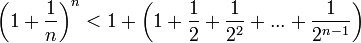Сумму в скобке найдём по формуле суммы членов геометрической прогрессии:

.

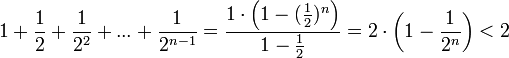Поэтому 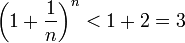(3).

Итак, последовательность ограничена сверху, при этом 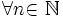выполняются неравенства (2) и (3): .

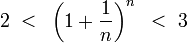Следовательно, на основании теоремы Вейерштрасса (критерий сходимости последовательности) последовательность 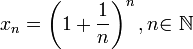монотонно возрастает и ограниченна, значит имеет предел, обозначаемый буквой e. Т.е.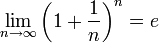

Зная, что второй замечательный предел верен для натуральных значений x, докажем второй замечательный предел для вещественных x, то есть докажем, что . Рассмотрим два случая:

1. Пусть . Каждое значение x заключено между двумя положительными целыми числами: , где — это целая часть x.

Отсюда следует: 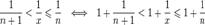, поэтому 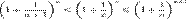.Если , то . Поэтому, согласно пределу 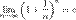, имеем:

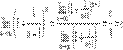
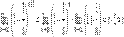.По признаку (о пределе промежуточной функции) существования пределов .

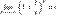2.Пусть 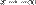. Сделаем подстановку − x = t, тогда

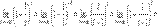
3. 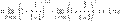.Из двух этих случаев вытекает, что 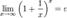для вещественного x.

Следствия

1.

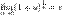
2.

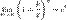
3.

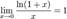
4.

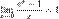
5. 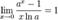для ,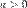

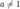
6.

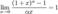
Примеры.

1. Функция f(x)=(x-1)² является бесконечно малой при x→1, так как 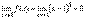(см. рис.).

2. Функция f(x) = tgx – бесконечно малая при x→0.

3. f(x) = ln (1+x)– бесконечно малая при x→0.

4. f(x) = 1/x– бесконечно малая при x→∞.

Установим следующее важное соотношение:

Теорема. Если функция y=f(x) представима при x→aв виде суммы постоянного числа b и бесконечно малой величины α(x): f (x)=b+ α(x) то .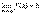

Обратно, если 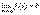, то f (x)=b+α(x), где a(x) – бесконечно малая при x→a.

Доказательство.

1. Докажем первую часть утверждения. Из равенства f(x)=b+α(x) следует |f(x) – b|=| α|. Но так как a(x) – бесконечно малая, то при произвольном ε найдется δ – окрестность точки a, при всех x из которой, значения a(x) удовлетворяют соотношению |α(x)|<ε. Тогда |f(x) – b|< ε. А это и значит, что .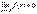

2. Если 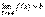, то при любом ε>0 для всех х из некоторой δ – окрестность точки a будет |f(x) – b|< ε. Но если обозначимf(x) – b= α, то |α(x)|<ε, а это значит, что a – бесконечно малая.

Рассмотрим основные свойства бесконечно малых функций.

Теорема 1. Алгебраическая сумма двух, трех и вообще любого конечного числа бесконечно малых есть функция бесконечно малая.

Доказательство. Приведем доказательство для двух слагаемых. Пусть f(x)=α(x)+β(x), где 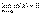и 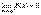. Нам нужно доказать, что при произвольном как угодно малом ε>0 найдется δ>0, такое, что для x, удовлетворяющих неравенству |x – a|<δ, выполняется |f(x)|< ε.

Итак, зафиксируем произвольное число ε>0. Так как по условию теоремы α(x) – бесконечно малая функция, то найдется такое δ₁>0, что при |x – a|<δ₁ имеем |α(x)|< ε/2. Аналогично, так как β(x) – бесконечно малая, то найдется такое δ₂>0, что при |x – a|<δ₂ имеем | β(x)|< ε/2.

Возьмем δ=min{ δ₁, δ₂}.Тогда в окрестности точки a радиуса δбудет выполняться каждое из неравенств |α(x)|< ε/2 и | β(x)|< ε/2. Следовательно, в этой окрестности будет

|f(x)|=| α(x)+β(x)| ≤ |α(x)| + | β(x)| < ε/2 + ε/2= ε,

т.е. |f(x)|<ε, что и требовалось доказать.

Теорема 2. Произведение бесконечно малой функции a(x) на ограниченную функцию f(x) при x→a (или при x→∞) есть бесконечно малая функция.

Доказательство. Так как функция f(x) ограничена, то существует число М такое, что при всех значениях x из некоторой окрестности точки a|f(x)|≤M. Кроме того, так как a(x) – бесконечно малая функция при x→a, то для произвольного ε>0 найдется окрестность точки a, в которой будет выполняться неравенство |α(x)|< ε/M. Тогда в меньшей из этих окрестностей имеем | αf|< ε/M= ε. А это и значит, что af – бесконечно малая. Для случая x→∞ доказательство проводится аналогично.

Из доказанной теоремы вытекают:

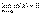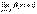Следствие 1. Если и , то .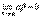

Следствие 2. Если 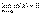и c=const, то .

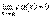Теорема 3. Отношение бесконечно малой функции α(x) на функцию f(x), предел которой отличен от нуля, есть бесконечно малая функция.

Доказательство. Пусть 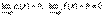. Тогда 1/f(x) есть ограниченная функция. Поэтому дробь 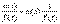есть произведение бесконечно малой функции на функцию ограниченную, т.е. функция бесконечно малая.

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция xsinx, неограниченная с обеих сторон, не является бесконечно большой при .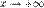

Последовательность a_n называется бесконечно большой, если .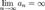

Функция называется бесконечно большой в окрестности точки x₀, если .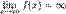

Функция называется бесконечно большой на бесконечности, если 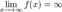либо .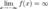

Свойства бесконечно малых

· Сумма конечного числа бесконечно малых — бесконечно малая.

· Произведение бесконечно малых — бесконечно малая.

· Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

· Если a_n — бесконечно малая последовательность, сохраняющая знак, то 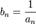— бесконечно большая последовательность.

Сравнение бесконечно малых.

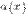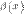Пусть и — бесконечно малые при .
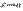1. Если 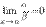, то говорят, что 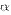является бесконечно малой высшего порядка по сравнению с 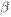. В этом случае пишут .
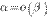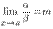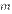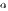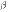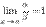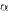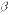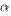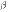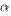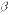2. Если , где —число, отличное от нуля, то говорят, что и — бесконечно малые одного и того же порядка. В частности, если , то бесконечно малые и называются эквивалентными. Запись ~ означает, что и —эквивалентные бесконечно малые. Если 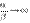, то это означает, что 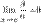. Таким образом, 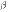является бесконечно малой высшего порядка по сравнению с 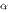, т. е.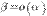
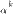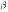3. Если и —бесконечно малые одного и того же порядка, причем 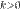, то говорят, что бесконечно малая 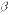имеет порядок 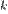по сравнению с .
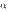Отметим некоторые свойства бесконечно малых величин:
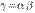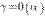1^o. Произведение двух бесконечно малых есть бесконечно малая высшего порядка по сравнению с сомножителями, т. е. если , то и .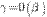
2^o. Бесконечно малые 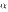и 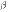эквивалентны тогда и только тогда, когда их разность 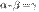является бесконечно малой высшего порядка по сравнению с 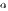и 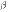, т. е. если , .
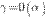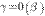3^o. Если отношение двух бесконечно малых имеет предел, то этот предел не изменится при замене каждой из бесконечно малых эквивалентной ей бесконечно малой, т.е. если
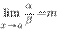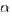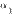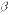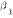, ~ , ~ , то .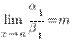

Полезно иметь в виду эквивалентность следующих бесконечно малых величин: если 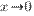, то

~ ~ ~ ~

~ ~

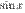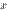
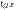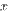
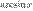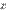
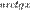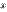
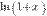
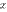
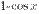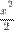
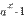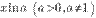
20. Непрерывность функций в точке. Точки разрыва.Представление о непрерывности функции интуитивно связано у нас с тем, что её графиком является плавная, нигде не прерывающаяся линия. При рассмотрении графика такой функции y = f(x) мы видим, что близким значениям аргумента соответствуют близкие значения функции : если независимая переменная приближается к точке x₀, то значение функции y = f(x) неограниченно приближается к значению функции в точкеx₀, т.е. к f(x₀).

Дадим строгое определение непрерывности функции . Итак, пусть имеем функцию y = f(x).

Функция y = f(x) называется непрерывной в точке x₀, если она определена в этой точке и в некоторой окрестности содержащей x₀ и 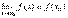Таким образом, можно сказать, что функция непрерывна в точкеx₀, если выполнены 3 условия:

1. она определена в точке x₀ и в некоторой её окрестности;

2. имеет предел при x → x₀;

3. этот предел равен значению функции в точке x₀.

Формулу (1) можно записать в виде 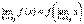, т.к. 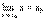. Это означает, что для того, чтобы найти предел непрерывной функции при x → x₀, достаточно в выражение функции подставить вместо аргументах его значение x₀.

Непрерывные функции обладают следующими свойствами.

Теорема 1. Если функции f(x) и g(x) непрерывны в точке x₀, то их сумма φ(x) = f(x) + g(x) также есть непрерывная функция в точке x₀.

Доказательство. Так как функции f(x) и g(x) непрерывны в точке x₀, то исходя из определения можно написать 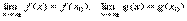. Тогда на основании свойств пределов будем иметь

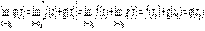.Эта теорема справедлива для любого конечного числа слагаемых.

Следующие две теоремы докажите самостоятельно аналогично теореме 1.

Теорема 2. Произведение двух непрерывных функций есть функция непрерывная.

Теорема 3. Частное двух непрерывных функций есть функция непрерывная, если знаменатель в рассматриваемой точке не обращается в нуль.

Если функцию можно представить в виде y = f(u), где u =φ(x), т.е. если функция зависит от переменной через промежуточный аргумент u, то называется сложной функцией переменной x.

Справедлива следующая теорема.

Теорема 4. Если функция u = φ(x) непрерывна в точкеx₀ и принимает в этой точке значение u₀ = φ(x₀), а функция f(u) непрерывна в точке u₀, то сложная функция y = f(φ(x)) непрерывна в точке x₀.

Используя эти теоремы можно доказать следующий результат.

Теорема 5. Всякая элементарная функция непрерывна в каждой точке , в которой она определена.

Заметим, что если функция y = f(x) непрерывна в точке x₀ и её значение в этой точке отлично от 0, f(x₀) ≠ 0, то значения функции f(x) в некоторой окрестности точки x₀ имеют тот же знак, что и f(x₀), т.е. если f(x₀) > 0, то найдётся такое δ > 0, что на интервале(x₀– δ;x₀+ δ) f(x) > 0 (в этой окрестности значения функции f(x) очень мало отличаются от своего предела).Определение. Функция 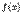имеет точку разрыва при 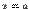, если она определена слева и справа от точки 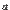, но в точке 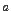не выполняется хотя бы одно из условий непрерывности.

Точки разрыва функции :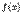

1. Точка устранимого разрыва;

2. Точка разрыва первого рода;

3. Точка разрыва второго рода.

Точка является точкой устранимого разрыва, если функция в точке 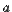не определена и существуют равные конечные пределы 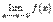и 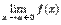, т.е. .

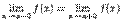Понятие производной

Рассмотрим задачу, которая приводит к понятию производной. Пусть функция u(t) выражает количество произведенной продукции за время t. Найдем производительность труда в момент t₀. За период от t₀ до t₀+Δ t количество продукции изменится от u(t₀) до u₀+Δ u = u(t₀+Δ t). Тогда средняя производительность труда за этот период z = Δ u/Δ t, поэтому производительность труда в момент t₀

z = lim_{D t® 0}D u/D t.

Определение 1 (производная).Производной функции y = f(x) в фиксированной точке x называется предел

lim_{D x® 0}D y/D x

при условии существования этого предела.

Производная обозначается следующим образом f'(x) или y'.

Определение 2.Правой (левой) производной называется правый (левый) предел

lim_{D x® 0 + 0}D y/D x lim_{D x® 0 - 0}D y/D x ,

если эти пределы существуют.

Для обозначения правой (левой) производной используют символ: f'(x+0) f'(x-0). Необходимым и достаточным условием существования производной является равенство f'(x+0) = f'(x-0).

Геометрический смысл производной

Рассмотрим график функции y = f(x), определенной и непрерывной на (a,b). Зафиксируем произвольную точку x на (a,b), и зададим приращение D x¹ 0, причем x+D x Î (a,b). Пусть точки M,P - точки на графике f(x), абсциссы которых равны x, x+D x (рис.21). Координаты точек M и P имеют вид M(x,f(x)), P(x+D x,f(x+D x). Прямую, проходящую через точки M, P графика функции f(x) будем называть секущей. Обозначим угол наклона секущей MP к оси ОX через f (D x). Определение 3.Если существует предельное положение секущей MP при стремлении точки N к точке M вдоль графика функции при D x® 0), то это предельное положение называется касательной к графику функции f(x) в данной точке M этого графика.

Из данного определения следует, что для существования касательной к графику f(x) в точке M достаточно, чтобы существовал предел lim_{D x® 0}f (D x) = f ₀, который равен углу, образованному касательной с положительным направлением оси OX. Справедливо утверждение:

Предложение 1.Если f(x) имеет в данной точке x производную, то существует касательная к графику функции f(x) в точке
M( x,f(x)) , причем угловой коэффициент этой касательной равен производной f'(x).

Из этого утверждения вытекает геометрический смысл производной: производная f'(x₀) есть угловой коэффициент касательной, проведенной к кривой y = f(x) в точке x₀, который в свою очередь равен tg угла наклона касательной к графику функции.

Тогда уравнение касательной к кривой f(x) в точке x₀ имеет вид

y = f(x₀)+f'(x₀)(x-x₀)

Определение 4 (дифференцируемость в точке).Функция f(x) называется дифференцируемой в точке x, если приращение D y этой функции в точке x представимо в виде

D y =AD x +a (D x) D x, (1)

где A - некоторое число, не зависящее от D x, а lim_{D x® 0} a (D x ) = 0.

В дальнейшем будем считать, что α(0) = 0. В этом случае функция Δ(x) будет непрерывной в точке Δ x = 0. Равенство 1 можно переписать иначе, так как функции Δ (Δ x), Δ x - бесконечно малые в точке Δ x = 0 и их произведение тоже бесконечно малая функция, поэтому

D y =AD x +o(D x).

(2)

Справедлива теорема

Теорема 1.Для того чтобы функция была дифференцируема в точке x, необходимо и достаточно, чтобы она имела в этой точке конечную производную.

Доказательство. Необходимость. Пусть функция дифференцируема, тогда ее приращение представимо в виде (1). Поделив (1) на Δ xΔ 0 получим

D y/D x = A+a(D x).

Переходя к пределу в последнем выражении при Δ x→ 0, получим, что A=f'(x).

Достаточность. Пусть существует конечная производная f'(x), то есть существует конечный предел

lim_{D x® 0}D y/D x = f'(x).

Обозначим α(Δ x) = Δ y/ Δ x-f'(x). Отсюда вытекает представление (1).

Теорема 2 (дифференцируемость и непрерывность).Если
функция дифференцируема в точке x, то она непрерывна в этой точке.

Доказательство. Так как функция дифференцируема в точке x, то то ее приращение представимо в виде (1), из которого следует, что lim_{D x® 0}D y = 0, что означает непрерывность функции в данной точке.

Заметим, что из непрерывности в данной точке не следует дифференцируемость в этой точке. Это видно из рассмотренного выше примера 4.

Производная непрерывной функции не обязательно непрерывна. Если функция имеет непрерывную производную на некотором множестве X, то функция называется гладкой на этом множестве. Если производная допускает конечное число точек разрыва (причем первого рода), то такая функция называется кусочно гладкой.

Правила дифференцирования

Приведем основные правила для нахождения производной:

1. Производная постоянной равна нулю, то есть c' = 0.

2. Производная алгебраической суммы конечного числа дифференцируемых функций равна такой же сумме производных этих функций, то есть

u(x) 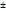v(x))' = u'(x) 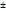v'(x).

3. Производная произведения двух дифференцируемых функций равна произведению производной первого сомножителя на второй плюс произведение первого сомножителя на производную второго, то есть

(u(x)v(x))' = u'(x)v(x)+u(x)v'(x).

Следствие 1.Постоянный множитель можно выносить за знак производной:

(cu(x))' = cu'(x).

4. Производная частного двух дифференцируемых функций может быть найдена по формуле

(u(x)/v(x))' = (u'(x)v(x)-u(x)v'(x))/v²(x)

при условии, что v(x)≠ 0.

ВЕРТИКАЛЬНЫЕ АСИМПТОТЫ

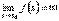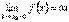Пусть при x→ x₀ с какой-либо стороны функция y = f(x)неограниченно возрастает по абсолютной величине, т.е. или или .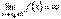

Тогда из определения асимптоты следует, что прямая x = x₀ является асимптотой. Очевидно и обратное, если прямая x = x₀ является асимптотой, т. о. .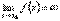

Таким образом, вертикальной асимптотой графика функции y = f(x) называется прямая, если f(x) → ∞ хотя бы при одном из условий x→ x₀ – 0 или x → x₀ + 0, x = x₀

Следовательно, для отыскания вертикальных асимптот графика функции y = f(x) нужно найти те значения x = x₀, при которых функция обращается в бесконечность (терпит бесконечный разрыв). Тогда вертикальная асимптота имеет уравнение x = x₀.

НАКЛОННЫЕ АСИМПТОТЫ

Поскольку асимптота – это прямая, то если кривая y = f(x) имеет наклонную асимптоту, то ее уравнение будет y = kx + b. Наша задача найти коэффициенты k и b.

Теорема. Прямая y = kx + b служит наклонной асимптотой при x → +∞ для графика функции y = f(x) тогда и только тогда, когда 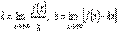. Аналогичное утверждение верно и при x → –∞.

Доказательство. Пусть MP – длина отрезка, равного расстоянию от точки M до асимптоты. По условию 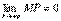. Обозначим через φ угол наклона асимптоты к оси Ox. Тогда из ΔMNP следует, что 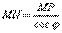. Так как φ постоянный угол (φ ≠ π/2), т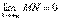о , но

MN = MK – NK = y - y_ас = f(x) - (kx+b).

Следовательно, мы можем записать следующее равенство .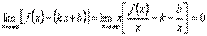

Так как x → +∞, то должно выполняться равенство 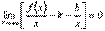. Но при постоянных k и b 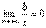и 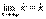. Следовательно, 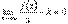, т.е.

Наши рекомендации