Почленное интегрирование или дифференцирование степенного ряда не меняют его радиус сходимости.

Доказательство. Под почленным интегрированием понимается интегрирование ряда 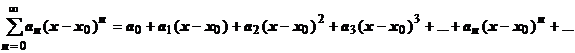по отрезку 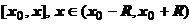. Результат этой операции: .

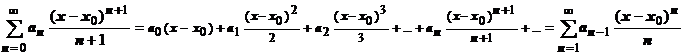Это тоже степенной ряд, его радиус сходимости 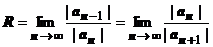равен радиусу сходимости исходного ряда.

Ряд, получающийся в результате почленного дифференцирования тоже степенной ряд: 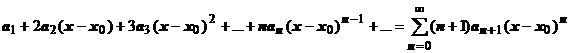. Его радиус сходимости 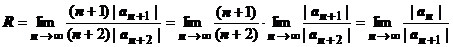тоже равен радиусу сходимости исходного ряда.

2. (Почленное интегрирование степенного ряда).Пусть сумма степенного ряда на области сходимости равна функции 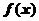, т.е. 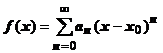. Тогда для .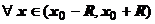

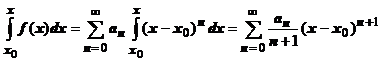Доказательство. Справедливость этого утверждения следует из равномерной сходимости степенного ряда на отрезке 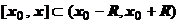иТеоремы 18.2.3.2 о почленном интегрировании равномерно сходящегося ряда.

3. (Почленное дифференцирование степенного ряда).Степенной ряд можно почленно дифференцировать в любой точке интервала сходимости, и .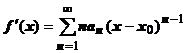

Доказательство. Справедливость этого утверждения следует из равномерной сходимости степенного ряда, составленного из производных членов исходного ряда, на любом отрезке, лежащем в интервале сходимости 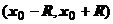иТеоремы 18.2.3.3 о почленном дифференцировании равномерно сходящегося ряда.

4. (Бесконечная дифференцируемость суммы степенного ряда).Сумма 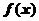степенного ряда в любой точке интервала сходимости имеет производные любого порядка; эти производные могут быть получены последовательным почленным дифференцированием исходного ряда.

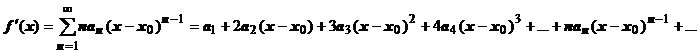
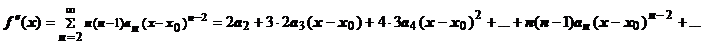
Доказательство. Справедливость этого утверждения следует из доказанной теоремы о почленном дифференцировании степенного ряда; последовательное применение этой теоремы даёт 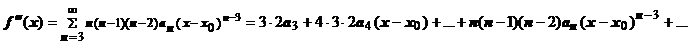и т.д.

18.2.5. Ряд Тейлора. Мы доказали, что сумма 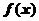степенного ряда в любой точке интервала сходимости бесконечно дифференцируема. Выразим коэффициенты ряда через производные суммы (похожую задачу мы решали в разделе 7.7. Формула Тейлора).

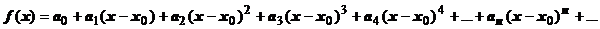. Положим здесь 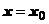. Все члены ряда, кроме нулевого, исчезают, и .

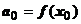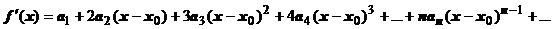. Положим 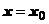, тогда .

. .

. .

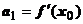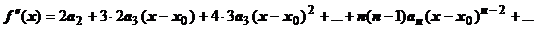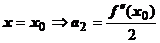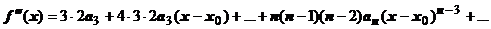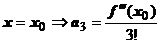Продолжая этот процесс, получим 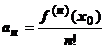. Заменив коэффициенты полученными выражениями, представим ряд как

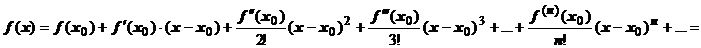
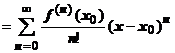. Ряд, стоящий в правой части этой формулы, называется рядом Тейлора функции 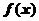. В частном случае, когда 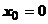и ряд принимает вид

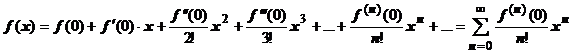, его принято называть рядом Маклорена. Напомним, что эти ряды получены в предположении, что 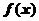- сумма степенного ряда и х - точка интервала сходимости.

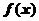Теперь рассмотрим обратную задачу: какой должна быть функция , чтобы её можно было представить в виде суммы степенного ряда? Первое, что очевидно, это то, что 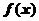должна быть бесконечно дифференцируемой функцией (так как сумма ряда бесконечно дифференцируема). Второе - то, что коэффициенты ряда должны быть равны 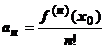. Поэтому предположим, что дана бесконечно дифференцируемая функция 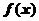, мы нашли коэффициенты ряда по формуле 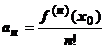, составили формальный ряд 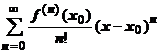и нашли область его сходимости. Будет ли сумма этого ряда на области сходимости равна 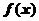? Это тот вопрос, которым мы будем заниматься дальше.

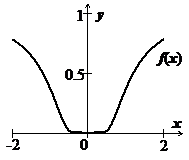
Приведём пример, когда ряд Маклорена функции 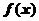сходится не к 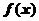, а к другой функции. Пусть 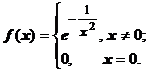Мы докажем, что все производные этой функции в точке х=0 равны нулю. При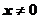 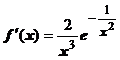. . 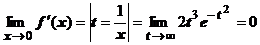Такие неопределённости придётся раскрывать при вычислении любой производной; заменой t=1/x они сводятся к неопределённостям, содержащим степенные и показательные функции, значение предела во всех случаях определяется пределом показательной функции и равно нулю. Значение производной в точке х=0 находим по определению производной:

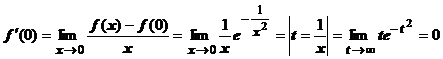. Итак, производная непрерывна в точке х=0 и равна нулю. 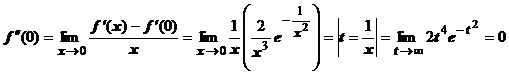и т.д. Так доказывается, что все производные в точке х=0 равны нулю. Как следствие, все коэффициенты ряда Тейлора этой функции равны нулю, и на всей числовой оси ряд сходится к функции, тождественно равной нулю, а не к .

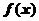Сформулируем условия, при которых ряд Тейлора функции 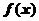сходится к этой функции. Эти условия удобно сформулировать в терминах остаточного члена формулы Тейлора. Напомним результаты раздела 7.7. Формула Тейлора: если 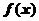имеет в окрестности точки 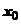все производные до n+1-го порядка включительно, то 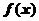может быть представлена в виде формулы Тейлора с остаточным членом в форме Лагранжа: 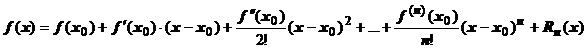, где 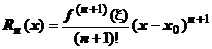- остаточный член в форме Лагранжа; 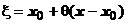- точка, расположенная между х и , .

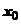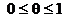Теорема.Для того, чтобы бесконечно дифференцируемая функция 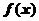в окрестности точки 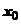разлагалась в ряд Тейлора, необходимо и достаточно, чтобы .

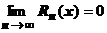Доказательство. Необходимость.Пусть в окрестности точки 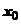функция 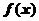представлена в виде сходящегося к этой функции ряда Тейлора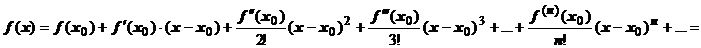 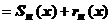, где 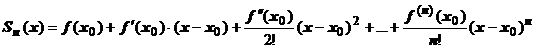- частичная сумма ряда, 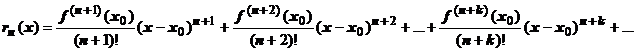- его остаток. Так как 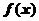имеет требуемое количество производных, она может быть представлена и в виде формулы Тейлора с остаточным членом в форме Лагранжа: 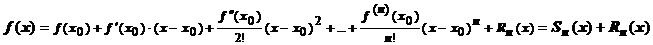. Сравнивая эти представления, получаем 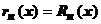. Из сходимости ряда к 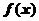следует, что 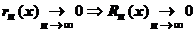, что и требовалось доказать.

Достаточность.Если 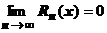, то 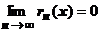, т.е. остаток ряда стремится к нулю при 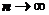, т.е. ряд сходится к функции .

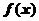Применения степенных рядов.

18.2.6.3.1. Приближённое вычисление значений функций. Идея таких вычислений простая. Пусть известно значение функции в точке 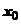, и функция разлагается в окрестности точки 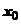в ряд Тейлора. Тогда значение функции в точке 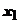, которое надо найти, равно 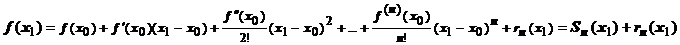, и принимается 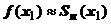. Естественно, мы должны гарантировать, что погрешность такого приближения не превышает заданной величины 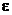. Погрешность равна остатку ряда после n-го члена (или остаточному члену формулы Тейлора), поэтому необходимо строить оценку сверху для 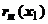(или 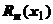). При оценке 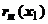принципиально отличны два случая. Если остаток - знакочередующийся ряд, то 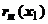просто оценивается по своему первому члену. Если остаток не является знакочередующимся рядом, то необходимо оценивать всю его сумму. Обычно в этом случае остаток мажорируют сходящейся геометрической прогрессией. В разделе 18.4.2. Знакочередующиеся рядымы рассмотрели и тот, и другой случай при нахождении значени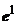й и 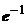; в разделе 7.9.2. Приближённые вычисления с помощью формулы Тейлораприведён пример вычисления значения 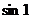с погрешностью 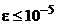. Другие примеры будут рассмотрены ниже.

Интегрирование функций.

1. Как мы знаем, интеграл 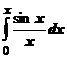аналитически не берётся. Это специальная функция, называемая интегральным синусом и обозначаемая 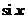. Получим разложение этой функции в степенной ряд. 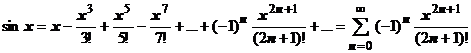, , 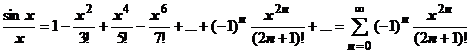почленно интегрируем: 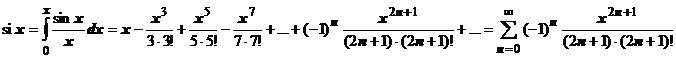. Ряд сходится к 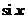при 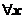. Теперь легко вычислить значение этой функции в любой точке. Пусть, например, надо найти 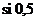с погрешностью 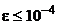. . 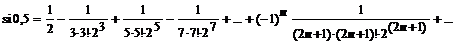Ряд знакочередующийся, первый член, меньший 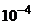, третий, поэтому .

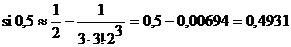2. Найти 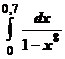. Этот интеграл берётся аналитически. Надо разложить знаменатель на множители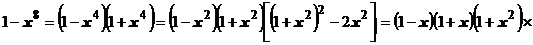

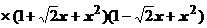, разложить подынтегральную функцию на пять простых дробей, найти восемь неопределённых коэффициентов и т.д., и после этого вычислять значение первообразной в начальной и конечной точках. Поступим по другому. Разложим подынтегральную функцию в ряд Маклорена и почленно проинтегрируем: 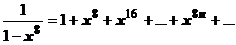, 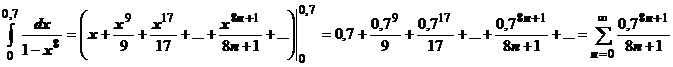. Остаток ряда после n-го члена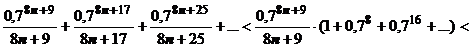 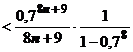. Если 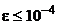, достаточно взять n=2, и .

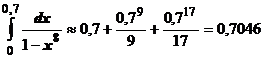18.2.6.3.3. Интегрирование дифференциальных уравнений с помощью степенных рядов. Пусть дана задача Коши: ,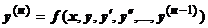

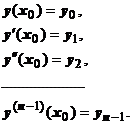
Решение этой задачи в виде ряда Тейлора ищется так. 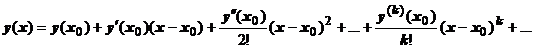. Первые n коэффициентов ряда известны из начальных условий, остальные находятся последовательным дифференцированием уравнения.

Примеры. 1. 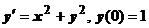. Из уравнения находим 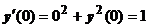. Дифференцируем уравнение: 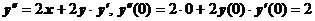. Далее дифференцируем уравнение и находим значение производной в точке 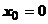: 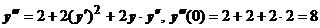, 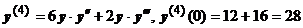. Так мы можем вычислить производные любого порядка. Решение задачи Коши: .

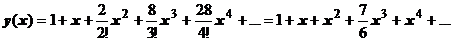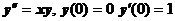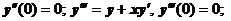
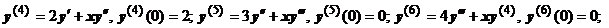
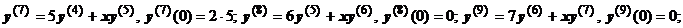
2. . Находим: 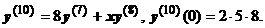Закономерность понятна. Производные порядка 3n-1 и 3n равны нулю, производная порядка 3n+1 равна 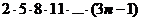, поэтому 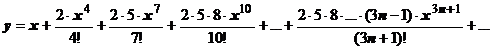С помощью признака Даламбера легко убедится, что этот ряд сходится при 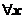, следовательно, даёт решение задачи Коши на всей числовой оси.