Свойства равномерно сходящихся рядов.

18.2.3.1. Теорема о непрерывности суммы равномерно сходящегося ряда непрерывных функций.Если члены функционального ряда 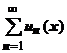- непрерывные функции, и этот ряд равномерно сходится на отрезке 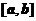, то сумма этого ряда непрерывна на .

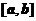18.2.3.2. Теорема о почленном интегрировании равномерно сходящегося ряда. Пусть члены функционального ряда непрерывны на отрезке 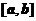, и ряд равномерно сходится к своей сумме 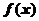на этом отрезке: 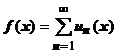. Тогда 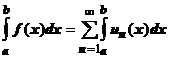, т.е. интеграл от суммы ряда равен сумме ряда, составленного из интегралов от членов равномерно сходящегося ряда.

18.2.3.3. Теорема о почленном дифференцировании равномерно сходящегося ряда. Пусть члены сходящегося ряда 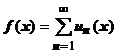- дифференцируемые на отрезке 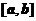функции, и ряд, составленный из производных 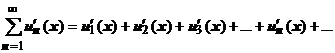, равномерно сходится на 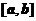. Тогда ряд 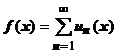можно почленно дифференцировать, и 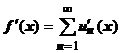, т.е. производная суммы ряда равна сумме ряда из производных.

Отметим тонкость, заключённую в этой теореме: для того, чтобы ряд можно было почленно дифференцировать, требуется равномерная сходимость не самого этого ряда, а ряда, составленного из производных его членов.

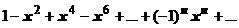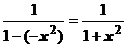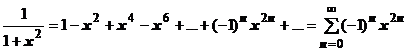Эти свойства равномерно сходящихся рядов по нашей программе принимаются без доказательства; мы будем ими пользоваться при изучении степенных рядов. Однако уже сейчас мы можем сделать из этих теорем тонкие и важные выводы. Ряд - геометрическая прогрессия со знаменателем , поэтому его сумма равна : . Мы доказали, что этот ряд равномерно сходится на любом отрезке 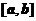, целиком лежащем в области сходимости (-1,1), поэтому его можно почленно проинтегрировать в пределах от 0 до 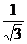: 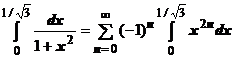. Вычисляя интегралы, получаем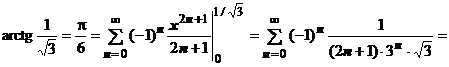 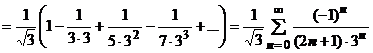. Это не только неожиданное и красивое представление числа 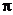в виде ряда 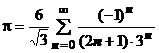, но и удобный способ его вычисления с любой точностью с простой оценкой остатка по первому отброшенному члену, так как получен ряд Лейбницевского типа (см. раздел 18.1.4.2).

Степенные ряды.

18.2.4.1. Определение.Степенным рядом называется функциональный ряд вида ,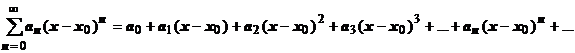

где 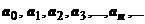- постоянные (коэффициенты ряда), 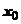- фиксированное число (центр сходимости). Степенной ряд имеет по меньшей мере одну точку сходимости - точку .

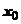Все содержательные сведения о степенном ряде содержатся в теореме Абеля.

18.2.4.2. Теорема Абеля.Если степенной ряд сходится в точке 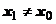, то

1. он абсолютно сходится в любой точке х, удовлетворяющей неравенству 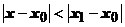(т.е. находящейся ближе к точке 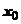, чем );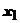

2. он сходится равномерно на любом отрезке 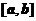, целиком лежащем на интервале 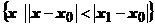(т.е. на интервале с центром в 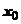радиуса ).

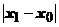3. Если этот ряд расходится в точке 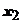, то он расходится в любой точке х, удовлетворяющей неравенству 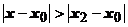(т.е. находящейся дальше от точки 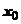, чем ).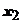

Доказательство. 1.Из сходимости ряда 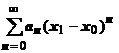в точке 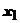следует, что его общий член 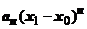стремится к нулю при 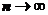; любая последовательность, имеющая предел, ограничена, следовательно, существует число С такое, что 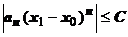. Пусть точка х удовлетворяет неравенству 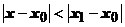, тогда 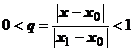. Оценим член ряда в точке х:

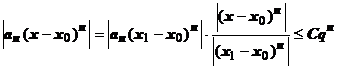. Члены ряда в точке х по абсолютной величине не превосходят членов сходящейся геометрической прогрессии, следовательно, ряд сходится абсолютно в точке х, следовательно, он сходится абсолютно в любой точке интервала .

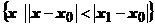2. Пусть отрезок 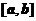, целиком лежит на интервале 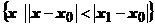. Из точек а, b выберем ту, которая находится дальше от точки 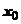, примем для определённости, что это - точка а: 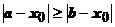. Тогда для любого х из этого отрезка 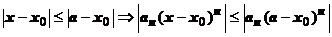. В точке 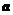ряд 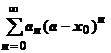, по доказанному, сходится абсолютно, но он является на 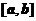мажорантой для ряда 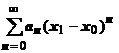, следовательно, степенной ряд сходится равномерно на отрезке .

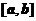3. Пусть степенной ряд расходится в точке 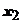, и 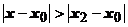. То, что ряд расходится в точке х, докажем от противного. Если предположить, что он сходится в точке х, то, по доказанному, он сходится во всех точках, расположенных ближе к 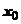, чем х, следовательно, он сходится в точке 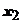, что противоречит условию.

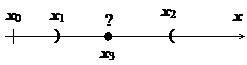18.2.4.3. Радиус сходимости, интервал сходимости и область сходимости степенного ряда.Из теоремы Абеля следует, что существует такое число R 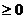(возможно, 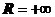) такое, что при 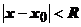степенной ряд сходится, при 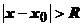ряд расходится. Действительно, пусть в точке 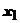ряд сходится, в точке 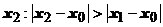ряд расходится. Рассмотрим точку 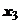, расположенную между областями, в которых установлена сходимость и расходимость. В точке 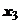числовой ряд 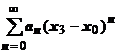либо сходится, либо расходится. Если он сходится, то мы можем перенести точку 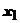в точку 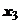; если ряд в точке 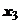расходится, мы переносим в 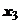точку 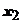. Продолжая этот процесс, мы сблизим точк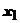и и 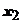, эта граница и определит число R.

Определение. Число R 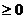такое, что при 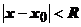степенной ряд сходится, при 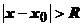ряд расходится, называется радиусом сходимости. Интервал 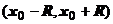называется интервалом сходимости степенного ряда.

Сходимость ряда в концевых точках интервала сходимости должна исследоваться отдельно. В зависимости от поведения ряда на концах интервала сходимости область сходимости степенного ряда может быть одной из следующих: , , , .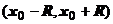

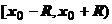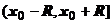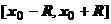Итак, для определения области сходимости степенного ряда надо найти его интервал сходимости R, затем исследовать поведения ряда в концевых точках интервала сходимости 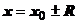.