Аналитическая геометрия: прямая и плоскость. Кривые второго порядка. Уравнение линии в полярных координатах.

Задание 1.

1. Уравнение прямой 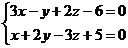записать в каноническом и параметрическом видах.

2. Написать уравнение прямой, проходящей через точку пересечения прямых х + 4у – 5 = 0 и 7х + 5у + 11 = 0 и точку А(5;0).

3. Написать уравнение прямой, проходящей через точку А(2;-3;-4) и параллельно прямой: .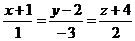

4. Доказать что прямые l₁ и l₂ параллельны,

.

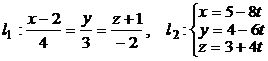5. Определить угол φ, образованный двумя прямыми: 3х – у + 5 = 0 и

2х + у – 7 = 0.

6. Написать каноническое уравнение прямой, проходящей через точку А(2;0;-1) параллельно прямой х = -2 + t, у = 2t, z = 1-t/2.

7. Показать, что прямая 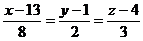лежит в плоскости

х+2у–4z+1=0.

8. Составить параметрические уравнения прямой, проходящей через точки А(-5;3;-2) и В(-3;2;-2).

9. Составить параметрические уравнения прямой, проходящей через точку М₁(-2;3;5) перпендикулярно плоскости 3х + 5у – 6z – 11 = 0.

10. Найти угол между прямой 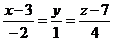и плоскостью 3х+2у–4z+12=0.

11. Дана прямая 2х + 3у + 4 = 0. Составить уравнение прямой, проходящей через точку М₀(2;1) под углом в 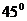к данной прямой.

12. Найти угол между прямыми: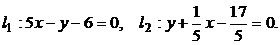

13. Найти точку пересечения прямой и плоскости: ;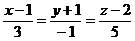

14. Написать уравнение плоскости, параллельной плоскости х-2у+2z+5=0 и удаленной от точки М(3;4;-2) на расстоянии d = 5.

15. Доказать что прямые l₁ и l₂ параллельны

.

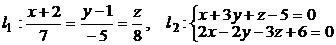16. Написать уравнение прямой, проходящей через точку пересечения прямых х + 2у + 3 = 0, 2х + 3у + 4 = 0, параллельно прямой 5х + 8у = 0.

17. Найти точку пересечения прямой и плоскости: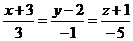

х – 2у + z – 15 = 0.

18. Написать уравнение плоскости, проходящей через точку Р(2;0;-1) и точку М(1;-1;3), перпендикулярно к плоскости 3х + 2у – z = 15.

19. Из точки А(-1;-1;4) опущен на плоскость перпендикуляр; его основание В(2;4;5). Найти уравнение плоскости и уравнение перпендикуляра.

20. Найти угол между плоскостями α и β, если α: х – у + 1 = 0, β: у – z+1=0.

21. Составить уравнение плоскости, проходящей через т. М₁(2;3;-1) и М₂(1;0;3), перпендикулярно плоскости 3х – у + 3z + 2 = 6.

22. Составить уравнение плоскости, проходящей через прямую: 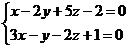и точку М(2;-3;-4).

23. Составить уравнение плоскости, проходящей через две точки А(-2;1;-3) и В (1;3;-2), параллельной вектору 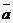= (-2;2;-1).

24. Составьте уравнение плоскости, которая проходит через точку

А(2;-1;1) перпендикулярно к двум плоскостям 2х – z + 1 = 0 и у = 0.

25. Написать уравнение плоскости, проходящей через точки М₁(1;1;1) и М₂(-1;1;-1) параллельно прямой, соединяющей точки А(5;-2;3) и В(6;1;0).

26. Написать уравнение плоскости, проходящей через точку М₀(2;-1;-3), перпендикулярно линии пересечения плоскостей х+у–z+5=0, 2х–у+2z–2=0.

27. Написать уравнение плоскости, проходящей через прямую 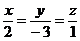и точку М₀(4;-3;2).

28. Написать уравнение плоскости, проходящей через точку М₀(2;-3;1) параллельно векторам , .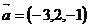

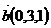29. Написать уравнение плоскости, проходящей через пару параллельных прямых 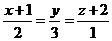и .

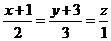30. Написать уравнение плоскости, проходящей через точку А(1;-2;4) и перпендикулярно к прямой .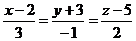

Задание 2.

1. Уравнение одной из сторон квадрата х + 3у – 5 = 0. Составить уравнения трех остальных сторон квадрата, если Р(-1;0) - точка пересечения его диагоналей. Сделать чертеж.

2. Даны уравнения одной из сторон ромба х – 3у + 10 = 0 и одна из его диагоналей х + 4у - 4 = 0; диагонали ромба пересекаются в точке Р(0;1). Найти уравнения остальных сторон ромба. Сделать чертеж.

3. Уравнения двух сторон параллелограмма х + 2y + 2 = 0 и х + у – 4 = 0, а уравнение одной из его диагоналей х - 2 = 0. Найти координаты вершин параллелограмма. Сделать чертеж.

4. Даны две вершины А(-3;3), В(5;-1) и точка D(4;3) пересечения высот треугольника. Составить уравнения его сторон. Сделать чертеж.

5. Даны вершины А(-3;-2), В(4;-1), С(1;3) трапеции АВCD (AD||BC). Известно, что диагонали трапеции взаимно перпендикулярны. Найти координаты вершины D этой трапеции. Сделать чертеж.

6. Даны уравнения двух сторон треугольника 5х – 4у + 15 = 0 и 4х+y–9=0. Его медианы пересекаются в точке Р(0;2). Составить уравнение третьей стороны треугольника. Сделать чертеж.

7. Даны две вершины А(2;-2) и В(3;-1) и точка Р(1;0) пересечения медиан треугольника ABC. Составить уравнение высоты треугольника, проведенной через третью вершину С. Сделать чертеж.

8. Даны уравнения двух высот треугольника x + y = 4 и у=2х и одна из его вершин А(0;2). Составить уравнения сторон треугольника. Сделать чертеж.

9. Даны уравнения двух медиан треугольника х – 2у+1=0 и у - 1=0 и одна из его вершин А(1;3). Составить уравнения его сторон. Сделать чертеж.

10. Две стороны треугольника заданы уравнениями 5х-2у-8=0 и 3х-2у–8=0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны. Сделать чертеж.

11. Составить уравнение и построить линию, расстояния каждой точки которой от начала координат и от точки А (5;0) относятся как 2:1.

12. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(-1;0) вдвое меньше расстояния ее от пряной х = -4.

13. Составить уравнение и построить линию, расстояния каждой точки которой от точки А(2;0) и от прямой 5х + 8 = 0 относятся, как 5:4.

14. Составить уравнение и построить линию, каждая точка которой находится вдвое дальше от точки А(4;0), чем от точки В(1;0).

15. Составить уравнение и построить линию, расстояния каждой точки которой от точки А(2;0) и от пряной 2х + 5 = 0 относятся, как 4:5.

16. Составить уравнение и построить линию, расстояние каждой точки которой от точки А(3;0) вдвое меньше расстояния от точки В (26;0).

17. Составить уравнение и построить линию, каждая точка которой одинаково удалена от точки А(0;2) и от прямой у – 4 = 0.

18. Составить уравнение и построить линию, каждая точка которой равноотстоит от оси ординат и от окружности х² + у² = 4х.

19. Составить уравнение и построить линию, каждая точка которой равноудалена от точки А(2;6) и от прямой у + 2 = 0.

20. Составить уравнение и построить линию, каждая точка которой отстоит от точки А(-4;0) втрое дальше, чем от начала координат.

21. В равнобедренном треугольнике АВС заданы вершины С(4;3), уравнение 2х – у – 5 = 0 основания АС и уравнение х – у = 0 боковой стороны (АВ). Написать уравнение стороны ВС.

22. Даны вершины треугольника: А(0;1), В(6;5), С(12;-1). Написать уравнение высоты треугольника, проведённой из вершины (А). Найти величину угла (А).

23. Даны вершины треугольника А(2;3), В(1;-2) и С(-3;2). Составить уравнение медианы (АD).

24. В треугольнике АВС координаты вершины В (2;-7). Уравнение высоты, опущенной из вершины А: 3х + у + 11 = 0. Написать уравнение стороны ВС.

25. Даны две вершины треугольника АВС А(-10;2), В(6;4), его высоты пересекаются в точке О(5;2). Определить координаты третьей вершины треугольника.

26. В равнобедренном треугольнике АВС заданы вершины С(4;3), уравнение 2х – у – 5 = 0 основания АС и уравнение х – у = 0 боковой стороны АВ. Написать уравнение стороны ВС.

27. Даны вершины треугольника: А(0;1), В(6;5), С(12;-1). Написать уравнение высоты треугольника, проведённой из вершины (А). Найти величину угла А.

28. В треугольнике АВС координаты вершины В(2;-7). Уравнение высоты, опущенной из вершины А: 3х + у + 11 = 0. Написать уравнение стороны ВС.

29. Даны вершины треугольника А(1;4), В(3;-9), С(-5;2). Определить длину его медианы, проведенной из вершины В.

30. Даны вершины треугольника А(3;6), В(-1;3), С(2;-1). Вычислить длину его высоты, проведенной из вершины С.

Задание 3.

1. Найти координаты центра и радиус окружности x² + y² – 4x +8у – 16 =0.

2. Найти координаты центра и радиус окружности 9x²+9y²–42x-54у–95=0.

3. Найти координаты центра и радиус окружности x² + y² – 4x + 6у – 3 = 0.

4. Найти координаты центра и радиус окружности x² + y² – x + 2у – 1 = 0.

5. Составить каноническое уравнение окружности, если ее центр лежит в точке С(-4;5) и окружность проходит через точку М(-1;1).

6. Составить уравнение хорды окружности x² + y² = 49, делящейся в точке А(1;2) пополам.

7. Составить каноническое уравнение окружности, проходящей через точки А(5;0) и В(1;4), если ее центр лежит на прямой х + у – 3 = 0.

8. Преобразовать уравнение 4x² + 3y² – 8x + 12y – 32 = 0 в каноническое уравнение эллипса, найти его полуоси, координаты центра и эксцентриситет. Построить линию.

9. Составить каноническое уравнение эллипса, зная, что расстояние между фокусами 2с = 10, а большая ось 2а = 16. Построить линию.

10. Составить каноническое уравнение эллипса, зная, что малая полуось в=4, а расстояние между фокусами 2с = 10. Построить линию.

11. Составить каноническое уравнение эллипса, зная, что большая полуось

а = 12, а эксцентриситет ε = 0,5. Построить линию.

12. Составить каноническое уравнение эллипса, зная, что сумма полуосей

а + в = 12, а расстояние между фокусами 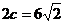. Построить линию.

13. Найти длины осей, координаты фокусов и эксцентриситет эллипса

4x² + 9y² = 144. Построить линию.

14. Составить уравнение эллипса, проходящего через точк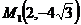и и 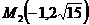. Построить линию.

15. Составить каноническое уравнение эллипса, фокусы которого расположены на оси Ох, симметрично относительно начала координат, зная что точка 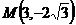принадлежат эллипсу, а эксцентриситет эллипса 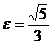. Построить линию.

16. Преобразовать уравнение 3x² + 12x - y² + 9 = 0 в каноническое уравнение гиперболы, найти ее полуоси, координаты фокусов, уравнения асимптот. Построить линию.

17. Уравнение асимптот гиперболы у = ±х/2, а расстояние между фокусами 2с=10. Найти каноническое уравнение гиперболы. Построить линию.

18. Составить каноническое уравнение гиперболы, фокусы которой находятся в точках F₁(-2,4) и F₂(12,4), а длина мнимой оси 26 = 6. Построить линию.

19. Составить каноническое уравнение гиперболы с фокусами на оси Ох, проходящей через точки М₁(6,-1) и 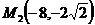. Построить линию.

20. Дано уравнение гиперболы 5x² - 4y² = 20. Найти: длины ее полуосей; координаты фокусов; эксцентриситет гиперболы; уравнение асимптот. Построить линию.

21. Эксцентриситет гиперболы 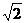. Составить каноническое уравнение гиперболы, проходящей через точку 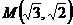. Построить линию.

22. Составить каноническое уравнение гиперболы, если ее фокусы лежат на оси Оу и расстояние между ними 2с = 10, а длина действительной оси 26=8. Построить линию.

23. Найти вершину, фокус и директрису параболы у = -2x² + 8х – 5. Построить график.

24. Дано уравнение гиперболы 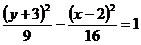. Найти: длины ее полуосей; координаты фокусов; эксцентриситет гиперболы; уравнение асимптот. Построить линию.

25. Найти вершину, фокус и директрису параболы у² + 4у - 24х + 76 = 0. Построить график.

26. Найти вершину, фокус и директрису параболы х = 5у² – 10у + 6. Построить график.

27. К параболе у² = 4х проведена касательная параллельно прямой

2х – у + 7 = 0. Найти уравнение этой касательной.

28. Камень, брошенный под углом к горизонту, достиг наибольшей высоты 16 м. Описав параболическую траекторию, он упал в 48 м от точки бросания. На какой высоте находился камень на расстоянии 6 м по горизонтали от точки бросания?

29. К параболе у² = 36х проведены из точки А(1;10) две касательные. Составить уравнение хорды, соединяющей точки касания.

30. Найти уравнение касательной к параболе у² = 4х, проведенной из точки А(-2;-1).

Задание 4.

Линия задана уравнением r = r(φ) в полярной системе координат, где r ≥ 0. Требуется: 1) построить линию по точкам начиная от φ = 0 до φ = 2π и придавая φ значения с шагом π/8; 2) найти уравнение данной линии в декартовой прямоугольной системе координат, у которой начало совпадает с полюсом, а положительная полуось абсцисс - с полярной осью; 3) по уравнению в декартовой прямоугольной системе координат определить, какая это линия. Построить линию.

1. r = 1/(1 + cosφ)

2. r = 4/(2 - 3cosφ)

3. r = 1/(2 + 2cosφ)

4. r = 10/(2 + cosφ)

5. r = 1/[3(1 - cosφ)]

6. r = 1/(2 + cosφ)

7. r = 8/(3 - cosφ)

8. r = 5/(3 - 4cosφ)

9. r = 3/(1 - 2cosφ)

10. r = 5/(6 + 3cosφ)

11. r = 2cos2φ

12. r = 2(1 + cosφ)

13. r = 2sin2φ

14.

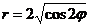
15.

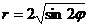
16. r = 2cos3φ

17. r = 2 + cosφ

18. r = 3(1 + cosφ)

19. r = 2sinφ

20. r = 6cosφ

21. r = cosφ – sinφ

22. r = cosφ + sinφ

23. r = 3/(1 + sinφ)

24. r = 15/(3 - 4cosφ)

25. r = 4/(1 - cosφ)

26. r = 16/(5 - 3cosφ)

27. r = 16/(5 + 3cosφ)

28. r = 9/(4 - 5cosφ)

29. r = 12/(2 - cosφ)

30. r = 10/(2 + sinφ)