Кривые второго порядка. Любое линейное уравнение задает на плоскости прямую

Любое линейное уравнение 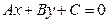задает на плоскости прямую. Линии, задаваемые уравнениями вида

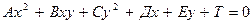, (4.12)

называются кривыми второго порядка. За исключением вырожденных случаев имеется всего 3 кривых второго порядка: эллипс (частный случай - окружность), гипербола и парабола, они имеют следующие канонические уравнения и вид.

1. Окружность

Окружностью радиуса 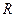с центром в точке 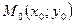называется множество точек плоскости удаленных от точки 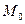на расстоянии .

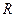Уравнение окружности имеет вид: 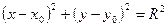. (4.13)

В частности, полагая, 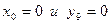получим уравнение окружности с центром в начале координат .

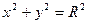1. Эллипс

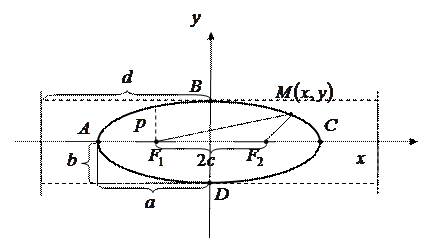
Эллипсом называется множество всех точек плоскости, сумма расстояний от каждой из которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.

Каноническое уравнение эллипса имеет вид:

Здесь

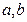- полуоси эллипса; О (0; 0) – центр эллипса. 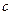- половина расстояния между фокусами. Вершины эллипса .

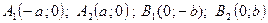Фокусы -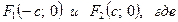

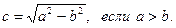Прямые 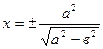называются директрисами эллипса.

Рис. 4.6

Форму эллипса характеризует отношение 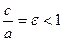, называемое эксцентриситетом эллипса. Чем меньше эксцентриситет, тем меньше вытянут эллипс вдоль фокальной оси, т.е. оси на которой лежат фокусы.

В предельном случае при 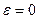эллипс переходит в окружность.

Если в каноническом уравнении эллипса 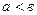, то фокусы располагаются на оси ОУ и имеют координаты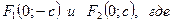

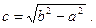
1. Гипербола

Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух фиксированных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Каноническое уравнение гиперболы имеет вид:

Здесь 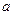- действительная полуось гиперболы, 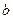- мнимая полуось гиперболы.

Точки 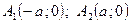- вершины гиперболы.

Фокусы гиперболы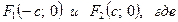

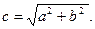
Гипербола имеет две асимптоты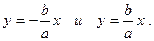

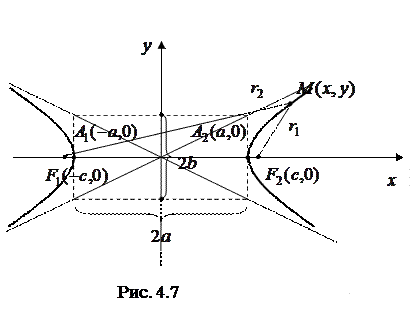
Для построения гиперболы сначала строят основной прямоугольник, ограниченный прямыми 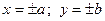, затем проводят его диагонали, которые совпадают с асимптотами гиперболы.

Форму гиперболы характеризует эксцентриситет 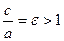. Чем меньше эксцентриситет, тем более вытянут её основной в направлении фокальной оси.

Гипербола 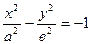называется сопряженной к гиперболе (4.15).

Здесь 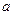- мнимая полуось гиперболы, 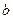- действительная полуось гиперболы Вершины сопряженной гиперболы 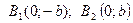и фокусы 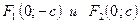лежат на оси ОY.

4. Парабола

Параболой называется множество всех точек плоскости, каждая из которых одинаково удалена от фиксированной точки, называемой фокусом и данной прямой, называемой директрисой. Расстояние от фокуса 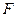до директрисы, называется параметром параболы и обозначается через .

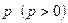Каноническое уравнение параболы имеет вид: 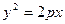, где 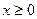. (4.16)

Точка 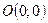- вершина параболы, ось 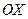- ось симметрии параболы.

Фокус 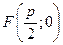и уравнение директрисы .

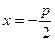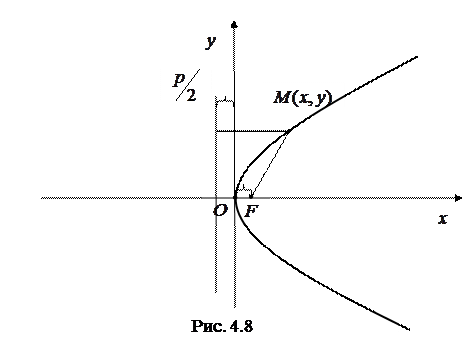
Парабола 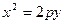располагается симметрично относительно оси .