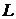Лекция 4. Прямая и плоскость. Кривые второго порядка
Лекция 4. Прямая и плоскость. Кривые второго порядка
Основные понятия о прямой
Прямая 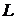 в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой).
в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой).
Пусть задана такая точка 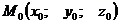 и вектор
и вектор 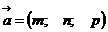 (Рис. 5.1).
(Рис. 5.1).
 |
Если 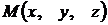 ‑ произвольная текущая точка прямой
‑ произвольная текущая точка прямой  , то вектор
, то вектор 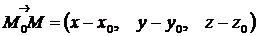 коллинеарен вектору
коллинеарен вектору  и их соответствующие координаты пропорциональны.
и их соответствующие координаты пропорциональны.
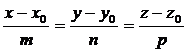 | (4.1) |
Этим соотношениям удовлетворяют координаты любой точки прямой  и только этой прямой. Равенства (4.1) называются каноническими уравнениями прямой в пространстве.
и только этой прямой. Равенства (4.1) называются каноническими уравнениями прямой в пространстве.
Обозначим 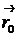 радиус-вектор точки
радиус-вектор точки 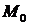 ,
, 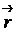 ‑ радиус-вектор точки
‑ радиус-вектор точки 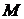 . Тогда:
. Тогда:
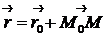 | (4.2) |
В силу коллинеарности векторов 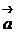 и
и 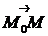 существует число
существует число 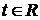 такое, что
такое, что 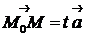 . Тогда из (4.2) получим векторное параметрическое уравнение прямой:
. Тогда из (4.2) получим векторное параметрическое уравнение прямой:
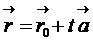 | (4.3) |
В координатной форме уравнение (4.3) равносильно трем уравнениям:
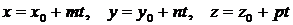 , , 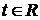 , , | (4.4) |
которые называются параметрическими уравнениями прямой в пространстве.
Исключая из уравнений (4.4) параметр 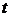 , легко перейти к каноническим уравнениям прямой (4.1).
, легко перейти к каноническим уравнениям прямой (4.1).
Обратный переход от (4.1) к (4.4) осуществляют, приравнивая каждое из трех соотношений (4.1) к 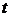 . При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
. При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
Пусть заданы точки 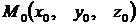 и
и 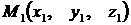 . Составим уравнение прямой, проходящей через заданные точки, пользуясь
. Составим уравнение прямой, проходящей через заданные точки, пользуясь
рис. 5.1.
Очевидно, что в этом случае направляющим вектором прямой 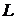 будет вектор
будет вектор 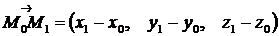 . Используя (4.1), получаем искомые уравнения в виде:
. Используя (4.1), получаем искомые уравнения в виде:
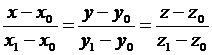 | (4.5) |
Прямую 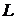 в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии
в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии 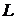 в общем виде:
в общем виде:
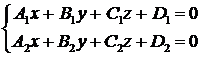 | (4.6) |
Система двух уравнений первой степени (4.6) определяет прямую линию при условии, что нормальные векторы 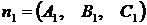 и
и 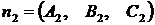 неколлинеарны. Только в этом случае плоскости будут пересекаться. Уравнения (4.6) носят название «общее уравнение прямой в пространстве».
неколлинеарны. Только в этом случае плоскости будут пересекаться. Уравнения (4.6) носят название «общее уравнение прямой в пространстве».
Чтобы перейти от общих уравнений прямой (4.6) к ее каноническим уравнениям (4.1), нужно на прямой найти какую-нибудь точку 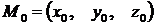 и определить ее направляющий вектор
и определить ее направляющий вектор 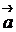 .
.
Точку 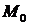 находят, давая произвольное значение одной из переменных
находят, давая произвольное значение одной из переменных 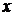 ,
, 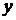 или
или 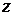 . Решая систему (4.6), получают значения оставшихся двух переменных.
. Решая систему (4.6), получают значения оставшихся двух переменных.
Направляющий вектор 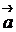 параллелен линии пересечения плоскостей (4.6) и, следовательно, перпендикулярен обоим нормальным векторам плоскостей:
параллелен линии пересечения плоскостей (4.6) и, следовательно, перпендикулярен обоим нормальным векторам плоскостей:
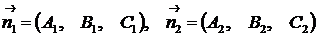 .
.
Поэтому в качестве 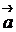 можно взять вектор:
можно взять вектор:
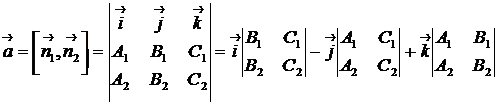
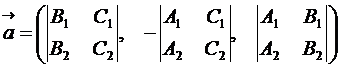 | (4.7) |
Основные понятия о плоскости
Всякая поверхность в пространстве задается в декартовых координатах уравнением вида 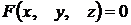 .
.
Если 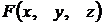 ‑ многочлен
‑ многочлен 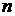 -й степени, то соответствующая поверхность называется алгебраической поверхностью
-й степени, то соответствующая поверхность называется алгебраической поверхностью 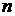 -го порядка или просто поверхностью
-го порядка или просто поверхностью 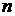 -го порядка.
-го порядка.
Всякая поверхность 1-го порядка есть плоскость, т.е. всякое уравнение 1-й степени:
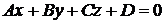 | (4.9) |
определяет плоскость. Уравнение (6.1) называется общим уравнением плоскости.
Вектор 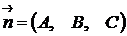 , координатами которого являются коэффициенты при
, координатами которого являются коэффициенты при 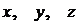 в уравнении (4.9), перпендикулярен плоскости (4.9) по свойству скалярного произведения векторов. Этот факт будет постоянно использоваться в дальнейшем. Вектор
в уравнении (4.9), перпендикулярен плоскости (4.9) по свойству скалярного произведения векторов. Этот факт будет постоянно использоваться в дальнейшем. Вектор 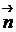 называют нормальным вектором плоскости (4.9).
называют нормальным вектором плоскости (4.9).
Уравнение плоскости, проходящей через данную точку 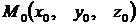 перпендикулярно вектору
перпендикулярно вектору 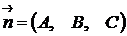 , имеет вид:
, имеет вид:
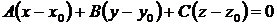 | (4.10 |
Очевидно, что уравнение (4.9) имеет смысл только тогда, когда хотя бы один из коэффициентов 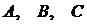 не равен нулю.
не равен нулю.
Рассмотрим частные случаи.
I. D ≠ 0.
1. Если 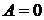 , то уравнение
, то уравнение 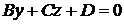 определяет плоскость, параллельную оси
определяет плоскость, параллельную оси 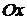 , так как вектор нормали к этой плоскости
, так как вектор нормали к этой плоскости 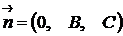 перпендикулярен оси
перпендикулярен оси 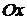 (проекция ненулевого вектора на ось равна нулю тогда, когда он перпендикулярен этой оси).
(проекция ненулевого вектора на ось равна нулю тогда, когда он перпендикулярен этой оси).
2. Аналогично, если 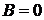 , то уравнение
, то уравнение 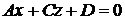 определяет плоскость, параллельную оси
определяет плоскость, параллельную оси 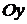 .
.
3. Если 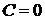 . То уравнение
. То уравнение 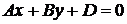 определяет плоскость, параллельную оси
определяет плоскость, параллельную оси 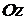 .
.
4. Если 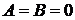 , то уравнение
, то уравнение 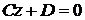 или
или 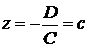 определяет плоскость, параллельную плоскости
определяет плоскость, параллельную плоскости 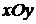 . В этом случае вектор нормали
. В этом случае вектор нормали 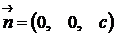 перпендикулярен к осям
перпендикулярен к осям 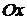 и
и 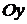 , т.е. к плоскости
, т.е. к плоскости 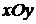 .
.
5. При 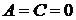 имеем
имеем 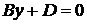 или
или 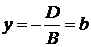 ‑ уравнение плоскости, параллельной координатной плоскости
‑ уравнение плоскости, параллельной координатной плоскости 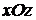 .
.
6. Если 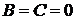 , то уравнение
, то уравнение 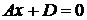 или
или 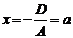 определяет плоскость, параллельную плоскости
определяет плоскость, параллельную плоскости 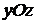 .
.
II. D = 0.
1. Если 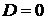 , то уравнение
, то уравнение 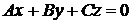 определяет плоскость, проходящую через начало координат, так как координаты точки
определяет плоскость, проходящую через начало координат, так как координаты точки 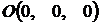 удовлетворяют этому уравнению.
удовлетворяют этому уравнению.
2. Если 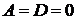 , то уравнение
, то уравнение 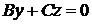 определяет плоскость, вектор нормали которой
определяет плоскость, вектор нормали которой 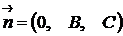 . Эта плоскость проходит через ось
. Эта плоскость проходит через ось 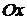 .
.
3. Аналогично, если 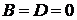 , то уравнение
, то уравнение 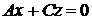 определяет плоскость, проходящую через ось
определяет плоскость, проходящую через ось  .
.
4. Если 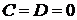 , то уравнение
, то уравнение 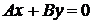 определяет плоскость, проходящую через ось
определяет плоскость, проходящую через ось 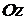 .
.
5. Если 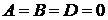 , то уравнение
, то уравнение 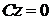 или
или 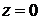 определяет плоскость
определяет плоскость 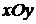 . Аналогично, уравнения
. Аналогично, уравнения 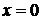 и
и 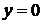 определяют соответственно плоскости
определяют соответственно плоскости 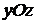 и
и 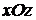 .
.
Если в уравнении (4.9) все коэффициенты 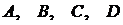 отличны от нуля, то это уравнение может быть преобразовано к уравнению плоскости в отрезках:
отличны от нуля, то это уравнение может быть преобразовано к уравнению плоскости в отрезках:
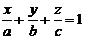 | (4.11) |
Здесь 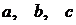 ‑ величины отрезков, отсекаемых плоскостью на осях координат.
‑ величины отрезков, отсекаемых плоскостью на осях координат.
Кривые второго порядка
Уравнение фигуры
Геометрической фигурой или просто фигурой на плоскости называется множество точек. Задать фигуру – значит указать, из каких точек плоскости она состоит. Одним из важных способов задания фигуры на плоскости является ее задание при помощи уравнений с двумя неизвестными. Произвольное уравнение с двумя неизвестными 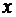 и
и 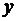 записывается в виде
записывается в виде 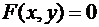 . Если выбрать на плоскости некоторую прямоугольную систему координат, то в ней уравнение называется уравнением фигуры
. Если выбрать на плоскости некоторую прямоугольную систему координат, то в ней уравнение называется уравнением фигуры 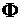 при выполнении следующих двух условий:
при выполнении следующих двух условий:
1. Если точка 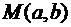 принадлежит фигуре
принадлежит фигуре 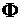 , то координаты
, то координаты 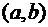 являются решениями уравнения
являются решениями уравнения 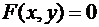 , т.е.
, т.е. 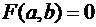 ;
;
2. если пара чисел 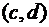 является решением уравнения
является решением уравнения 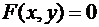 , то точка
, то точка 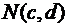 принадлежит фигуре
принадлежит фигуре 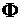 .
.
Это определение в более компактной записи выглядит следующим образом. Уравнение 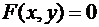 называется уравнением фигуры, если
называется уравнением фигуры, если 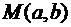
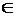
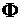
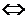
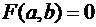 , то есть
, то есть 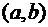 – решение уравнения
– решение уравнения 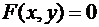 .
.
Из определения уравнения фигуры следует, что фигура 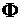 состоит только из тех точек плоскости, координаты которых являются решениями уравнения
состоит только из тех точек плоскости, координаты которых являются решениями уравнения  , т.е. уравнение фигуры задает эту фигуру.
, т.е. уравнение фигуры задает эту фигуру.
Возможны два вида задач:
1. дано уравнение 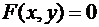 и надо построить фигуру
и надо построить фигуру 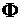 , уравнением которой является
, уравнением которой является 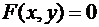 ;
;
2. дана фигура 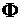 и надо найти уравнение этой фигуры.
и надо найти уравнение этой фигуры.
Первая задача сводится к построению графика уравнения 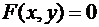 и решается, чаще всего, методами математического анализа.
и решается, чаще всего, методами математического анализа.
Для решения второй задачи, как следует из определения уравнения фигуры, достаточно:
1. Задать фигуру геометрически, т.е. сформулировать условие, которому удовлетворяют только точки фигуры (довольно часто определение фигуры содержит такое условие);
2. Записать в координатах условие, сформулированное в первом пункте.
Эллипс
Эллипсом называется линия, состоящая из всех точек плоскости, для каждой из которых сумма расстояний до двух данных точек 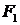 и
и 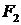 есть величина постоянная (большая, чем расстояние между
есть величина постоянная (большая, чем расстояние между 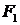 и
и 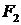 ).
).
Точки 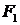 и
и 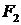 называются фокусами эллипса. Обозначив расстояние между фокусами через
называются фокусами эллипса. Обозначив расстояние между фокусами через 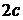 , а сумму расстояний от точек эллипса до фокусов через
, а сумму расстояний от точек эллипса до фокусов через 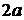 , имеем
, имеем 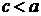 . Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.
. Если это условие не выполнено, то рассматриваемое множество точек либо отрезок прямой, заключенной между фокусами, либо не содержит ни одной точки.
Из определения эллипса вытекает следующий метод его построения: если концы нерастяжимой нити длины 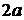 закрепить в точках
закрепить в точках 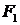 и
и 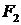 и натянуть нить острием карандаша, то при движении острия будет вычерчиваться эллипс с фокусами
и натянуть нить острием карандаша, то при движении острия будет вычерчиваться эллипс с фокусами 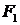 и
и 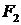 и с суммой расстояний от произвольной точки эллипса до фокусов, равной
и с суммой расстояний от произвольной точки эллипса до фокусов, равной 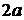
(Рис. 4.3).
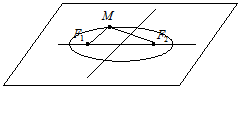
Рис. 4.3.
Составим уравнение эллипса. Для этой цели расположим декартову прямоугольную систему координат таким образом, чтобы ось 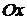 походила через фокусы
походила через фокусы 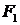 и
и 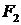 , положительное направление оси – от
, положительное направление оси – от 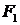 к
к 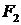 , начало координат выберем в середине отрезка
, начало координат выберем в середине отрезка 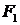
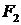 . Тогда координаты точек
. Тогда координаты точек 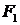 и
и 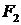 будут соответственно
будут соответственно 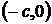 и
и 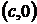 .
.
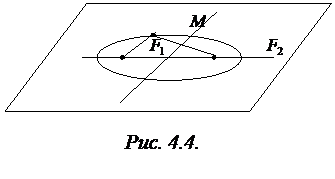 Пусть
Пусть 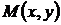 ‑ произвольная точка эллипса, тогда:
‑ произвольная точка эллипса, тогда: 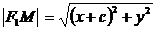 ,
, 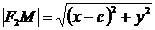 .
.
По определению эллипса 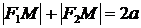 . Подставляя сюда значения
. Подставляя сюда значения 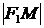 и
и 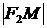 , имеем:
, имеем:
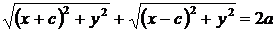 | (4.17) |
Уравнение (4.17) и есть уравнение эллипса. Преобразуя, упростим его:
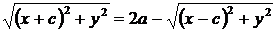
Возведя обе части уравнения в квадрат и приведя подобные члены, получим: 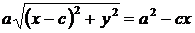 .
.
Возведем еще раз обе части в квадрат и приведем подобные члены. Получаем 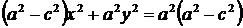 или
или
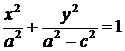 | (4.18) |
Положительную величину 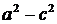 обозначим через
обозначим через 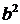 . Тогда уравнение (4.18) примет вид:
. Тогда уравнение (4.18) примет вид:
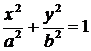 | (4.19) |
Оно называется каноническим уравнение эллипса.
Координаты точек эллипса ограничены неравенствами 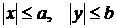 . Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами
. Значит, эллипс ограниченная фигура, не выходящая за пределы прямоугольника со сторонами 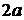 и
и 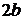 :
:
|
|
|
|
|
|
|
|
|
|




| |

|
|



|


|
| |
| |
| |
|

Заметим, что в уравнение (4.19) входят лишь четные степени 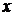 и
и 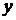 . Поэтому, если точка
. Поэтому, если точка 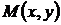 принадлежит эллипсу, то и точки
принадлежит эллипсу, то и точки 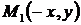 ,
, 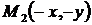 ,
, 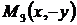 также ему принадлежат. А это означает, что эллипс – линия симметричная относительно координатных осей
также ему принадлежат. А это означает, что эллипс – линия симметричная относительно координатных осей 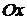 и
и 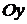 .
.
Поэтому для исследования формы эллипса достаточно рассмотреть его в первой координатной четверти, а в остальных четвертях его строение определяется по симметрии. Для первой четверти, из уравнения (4.19) имеем:
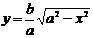 | (4.20) |
При возрастании 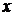 от
от 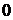 до
до 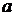 ,
, 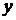 монотонно убывает от
монотонно убывает от 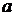 до
до 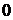 . График функции изображен на Рис. 4.6.
. График функции изображен на Рис. 4.6.
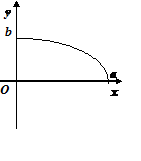
Рис. 4.6
Достроив остальные четверти эллипса по симметрии, получим весь эллипс (Рис.4.7).
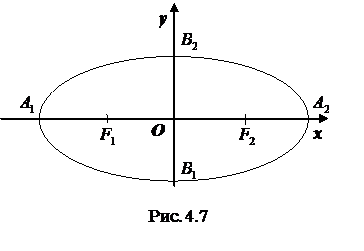
Оси симметрии эллипса (оси  и
и  ) называются просто его осями, а центр симметрии – точка
) называются просто его осями, а центр симметрии – точка  ‑ центром эллипса. Точки
‑ центром эллипса. Точки 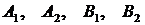 пересечения эллипса с осями координат называются вершинами эллипса. Отрезки
пересечения эллипса с осями координат называются вершинами эллипса. Отрезки 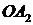 и
и 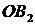 , а также их длины
, а также их длины 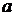 и
и 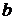 называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси
называются полуосями эллипса. В случае, когда фокусы эллипса находятся на оси 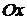 (как в нашем случае), из равенства
(как в нашем случае), из равенства 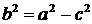 , следует, что
, следует, что 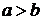 . В этом случае
. В этом случае 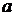 называется большой полуосью, а
называется большой полуосью, а 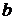 ‑ малой.
‑ малой.
Если 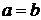 , то уравнение (4.19) можно переписать в виде:
, то уравнение (4.19) можно переписать в виде:
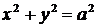 | (4.21) |
Это уравнение окружности с центром в начале координат. Эллипс можно получить из окружности сжатием плоскости к оси 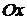 . Пусть на плоскости выбрана прямоугольная система координат
. Пусть на плоскости выбрана прямоугольная система координат 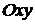 . Тогда преобразование, переводящее произвольную точку
. Тогда преобразование, переводящее произвольную точку 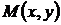 в точку
в точку 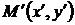 , координаты которой задаются формулами
, координаты которой задаются формулами 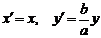 , будет окружность (4) переводить в эллипс, заданный соотношением
, будет окружность (4) переводить в эллипс, заданный соотношением 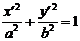 .
.

 Число
Число 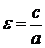 называется эксцентриситетом эллипса. Эксцентриситет
называется эксцентриситетом эллипса. Эксцентриситет 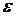 характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении
характеризует форму эллипса: чем ближе к нулю, тем больше эллипс похож на окружность; при увеличении 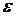 становится более вытянутым (Рис. 4.8).
становится более вытянутым (Рис. 4.8).
Фокальными радиусами точки 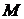 эллипса называются отрезки прямых, соединяющие эту точку с фокусами
эллипса называются отрезки прямых, соединяющие эту точку с фокусами 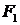 и
и 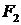 . Их длины
. Их длины 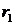 и
и 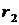 задаются формулами
задаются формулами 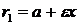 и
и 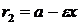 . Прямые
. Прямые 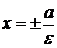 называются директрисами эллипса. Директриса
называются директрисами эллипса. Директриса 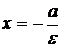 называется левой, а
называется левой, а 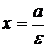 ‑ правой. Так как для эллипса
‑ правой. Так как для эллипса 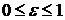 , то
, то 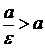 и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
и, следовательно, левая директриса располагается левее левой вершины эллипса, а правая – правее правой вершины.
Директрисы обладают следующим свойством: отношение расстояния 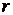 любой точки эллипса от фокуса к ее расстоянию
любой точки эллипса от фокуса к ее расстоянию 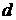 до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е.
до соответствующей директрисы есть величина постоянная, равная эксцентриситету, т.е. 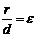 .
.
Гипербола
Гиперболой называется линия, состоящая из всех точек плоскости, модуль разности расстояний от которых до двух данных точек 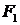 и
и 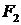 есть величина постоянная (не равная нулю и меньшая, чем расстояние между
есть величина постоянная (не равная нулю и меньшая, чем расстояние между 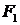 и
и 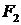 ).
).
Точки 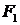 и
и 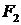 называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно
называются фокусами гиперболы. Пусть по-прежнему расстояние между фокусами равно 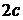 . Модуль расстояний от точек гиперболы до фокусов
. Модуль расстояний от точек гиперболы до фокусов 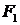 и
и 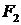 обозначим через
обозначим через 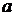 . По условию,
. По условию, 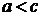 .
.
Выбрав декартову систему координат, как в случае эллипса, и используя определение гиперболы, составляем ее уравнение:
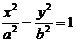 | (4.22) |
где 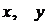 ‑ координаты произвольной точки гиперболы,
‑ координаты произвольной точки гиперболы, 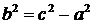 .
.
Уравнение (4.22) называется каноническим уравнением гиперболы.
Из уравнения (4.22) видно, что 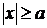 . Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми
. Это означает, что вся гипербола располагается вне полосы, ограниченной прямыми 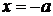 и
и 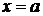 .
.
Так как в уравнение входят только четные степени 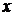 и
и 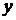 , то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (4.22) для первой четверти, имеем:
, то гипербола симметрична относительно каждой из координатных осей и начала координат. Поэтому достаточно построить эту кривую в первой четверти: в остальных четвертях гипербола строится по симметрии. Из уравнения (4.22) для первой четверти, имеем: 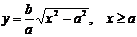 .
.
График этой функции от точки 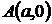 уходит неограниченно вправо и вверх (Рис. 4.9), и как угодно близко подходит к прямой:
уходит неограниченно вправо и вверх (Рис. 4.9), и как угодно близко подходит к прямой:
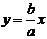 | (4.23) |
|
|


|
| |
|
|


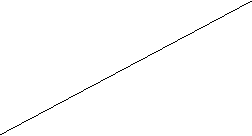
Поэтому говорят, что гипербола асимптоматически приближается к прямой (7.7), и эту прямую называют асимптотой гиперболы. Из симметрии гиперболы следует, что у нее две асимптоты 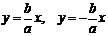 .
.
Построим гиперболу. Сначала строим, так называемый, основной прямоугольник гиперболы, центр которой совпадает с началом координат, а стороны равны 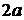 и
и 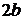 параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 4.10).
параллельны осям координат. Прямые, на которых расположены диагонали этого прямоугольника, являются асимптотами гиперболы. Сделаем рисунок гиперболы (Рис. 4.10).
|

Рис 4.10.
 Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки
Гипербола состоит из двух отдельных ветвей. Центр симметрии гиперболы называется ее центром, оси симметрии называются осями гиперболы. Точки 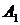 и
и 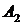 пересечения гиперболы с осью
пересечения гиперболы с осью 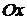 называются вершинами гиперболы. Величины
называются вершинами гиперболы. Величины 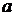 и
и 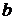 называются полуосями гиперболы. Если
называются полуосями гиперболы. Если 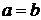 , то гипербола называется равносторонней.
, то гипербола называется равносторонней.
Эксцентриситетом гиперболы называется число 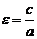 . Для любой гиперболы
. Для любой гиперболы 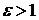 . Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси
. Эксцентриситет характеризует форму гиперболы: чем меньше, тем больше вытягивается гипербола вдоль оси 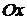 . На рисунке 4.11 изображены гиперболы с различными значениями
. На рисунке 4.11 изображены гиперболы с различными значениями 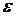 .
.


Рис. 4.11
Фокальными радиусами точки гиперболы называются отрезки прямых, соединяющие эту точку с фокусами 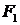 и
и 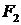 . Их длины
. Их длины 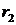 и
и 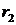 задаются формулами:
задаются формулами:
Для правой - ветви 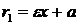 ,
,
Для левой - ветви 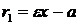 .
.
Прямые 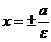 называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением
называются директрисами гиперболы. Как и в случае эллипса, точки гиперболы характеризуются соотношением 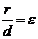 .
.
Парабола
Параболой называется линия, состоящая из всех точек плоскости, равноудаленных от данной точки 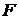 (фокуса) и данной прямой
(фокуса) и данной прямой 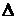 (директрисы).
(директрисы).
Для вывода канонического уравнения параболы ось 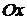 проводят через фокус
проводят через фокус 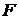 перпендикулярно директрисе
перпендикулярно директрисе 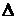 в направлении от директрисы к фокусу; начало координат берут в середине отрезка между фокусом
в направлении от директрисы к фокусу; начало координат берут в середине отрезка между фокусом 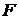 и точкой
и точкой 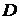 пересечения оси
пересечения оси 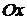 с директрисой
с директрисой 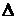 . Если обозначить через
. Если обозначить через 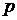 расстояние фокуса от директрисы, то
расстояние фокуса от директрисы, то 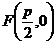 и уравнение директрисы будет иметь вид
и уравнение директрисы будет иметь вид 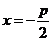 .
.
В выбранной системе координат уравнение параболы имеет вид:
 | (4.24) |
Это уравнение называется каноническим уравнением параболы. Из уравнения (4.24) видно, что 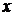 может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси
может принимать только неотрицательные значения. Значит, на рисунке вся парабола располагается справа от оси 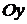 . Так как уравнение (4.24) содержит
. Так как уравнение (4.24) содержит 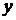 только в четной степени, то парабола симметрична относительно оси
только в четной степени, то парабола симметрична относительно оси 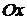 ,и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти
,и поэтому достаточно рассмотреть ее форму в первой четверти. В этой четверти 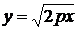 .
.
При неограниченном возрастании 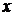 неограниченно растет и
неограниченно растет и 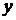 . Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии.
. Парабола, выходя из начала координат, уходит неограниченно вправо и вверх, четвертой четверти парабола строится по симметрии.
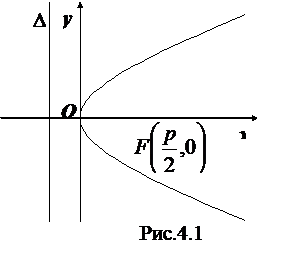 Сделаем рисунок параболы (Рис. 4.12).
Сделаем рисунок параболы (Рис. 4.12).
Ось симметрии параболы называется ее осью. Точка пересечения с ее осью называется вершиной параболы.
Лекция 4. Прямая и плоскость. Кривые второго порядка
Основные понятия о прямой
Прямая  в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой).
в пространстве может быть однозначно определена, если известна точка, принадлежащая прямой, и ненулевой вектор, параллельный прямой (направляющий вектор прямой).
Пусть задана такая точка 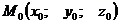 и вектор
и вектор 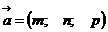 (Рис. 5.1).
(Рис. 5.1).
 |
Если 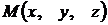 ‑ произвольная текущая точка прямой
‑ произвольная текущая точка прямой  , то вектор
, то вектор 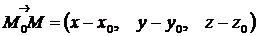 коллинеарен вектору
коллинеарен вектору  и их соответствующие координаты пропорциональны.
и их соответствующие координаты пропорциональны.
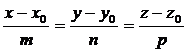 | (4.1) |
Этим соотношениям удовлетворяют координаты любой точки прямой  и только этой прямой. Равенства (4.1) называются каноническими уравнениями прямой в пространстве.
и только этой прямой. Равенства (4.1) называются каноническими уравнениями прямой в пространстве.
Обозначим 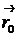 радиус-вектор точки
радиус-вектор точки  ,
, 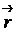 ‑ радиус-вектор точки
‑ радиус-вектор точки 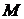 . Тогда:
. Тогда:
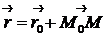 | (4.2) |
В силу коллинеарности векторов 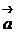 и
и 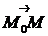 существует число
существует число 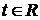 такое, что
такое, что 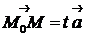 . Тогда из (4.2) получим векторное параметрическое уравнение прямой:
. Тогда из (4.2) получим векторное параметрическое уравнение прямой:
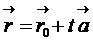 | (4.3) |
В координатной форме уравнение (4.3) равносильно трем уравнениям:
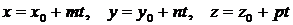 , , 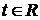 , , | (4.4) |
которые называются параметрическими уравнениями прямой в пространстве.
Исключая из уравнений (4.4) параметр 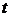 , легко перейти к каноническим уравнениям прямой (4.1).
, легко перейти к каноническим уравнениям прямой (4.1).
Обратный переход от (4.1) к (4.4) осуществляют, приравнивая каждое из трех соотношений (4.1) к 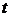 . При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
. При этом, если знаменатель какого-либо соотношения равен нулю, то необходимо приравнять к нулю его числитель.
Пусть заданы точки 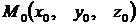 и
и 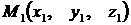 . Составим уравнение прямой, проходящей через заданные точки, пользуясь
. Составим уравнение прямой, проходящей через заданные точки, пользуясь
рис. 5.1.
Очевидно, что в этом случае направляющим вектором прямой  будет вектор
будет вектор 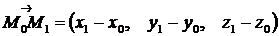 . Используя (4.1), получаем искомые уравнения в виде:
. Используя (4.1), получаем искомые уравнения в виде:
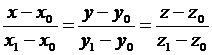 | (4.5) |
Прямую  в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии
в пространстве можно определить как пересечение двух плоскостей. Рассматривая совместно уравнения этих плоскостей, получим уравнение линии