Дифференцирование ФКП. Аналитические ФКП
Производной от функции комплексной переменной w = f (z) в точке z0 называется предел:
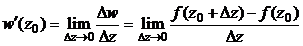 ,
,
где 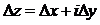 , и
, и 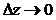 произвольным образом.
произвольным образом.
Функцию w = f (z), дифференцируемую в точке z0 и некоторой ее окрестности, называют аналитической,или регулярной функцией в точке z0.
Точки, в которых ФКП не является аналитической, называют особыми точками этой функции.
Для того, чтобы функция f (z) = u(x,y) +iv(x,y) была аналитической в области D необходимо и достаточно, чтобы частные производные 1-го порядка функций u(x, y) и v(x, y) были непрерывны в этой области и выполнялись бы условия:
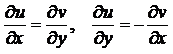 , (10)
, (10)
называемые условиями Эйлера-Даламбера, или условиями Коши-Римана.
Пример 5. Проверить аналитичность ФКП 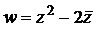 .
.
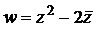 Þ u = x2 – y2 – 2x; v = 2xy + 2y (см. пример 1). Проверим выполнение условий Коши-Римана:
Þ u = x2 – y2 – 2x; v = 2xy + 2y (см. пример 1). Проверим выполнение условий Коши-Римана:
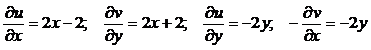 .
.
Условия (10) не выполняются, следовательно, эта функция не является аналитической.
Пример 6. Проверить аналитичность ФКП 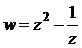 .
.
Выделим действительную и мнимую части функции:
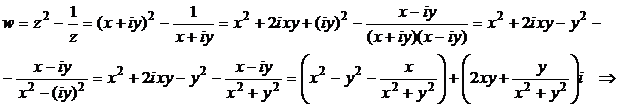
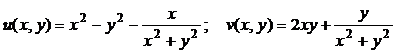 .
.
Проверим выполнение условий Коши-Римана:
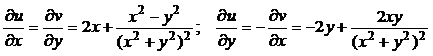 .
.
Условия выполняются во всех точках, кроме особой точки (0,0), в которой функции и u(x, y) и v(x, y) не определены. Следовательно, функция 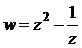 аналитическая при
аналитическая при 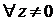 .
.
Если функция w = f (z) аналитическая в области D, то ее производную 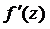 можно найти, используя правила дифференцирования, аналогичные правилам дифференцирования функции одной действительной переменной.
можно найти, используя правила дифференцирования, аналогичные правилам дифференцирования функции одной действительной переменной.
Пример 7. Вычислить значение производной функции 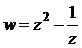 в точке
в точке
z0 = – 1+ i.
Функция 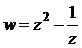 – аналитическая, а значит, дифференцируемая во всей своей области определения (см. пример 3). Ее производная:
– аналитическая, а значит, дифференцируемая во всей своей области определения (см. пример 3). Ее производная:
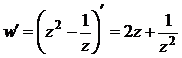 .
.
Вычислим значение производной в точке z0 = – 1+ i:
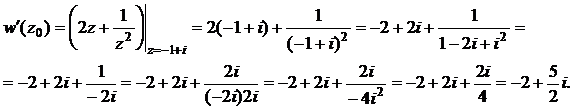
Следовательно, 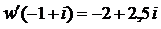 .
.
Задача 1. Даны уравнение 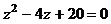 , комплексное число
, комплексное число 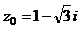 и натуральное число n = 6. Требуется:
и натуральное число n = 6. Требуется:
1) найти корни уравнения z1, z2 на множестве комплексных чисел;
2) найти комплексное число 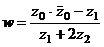 в алгебраической форме;
в алгебраической форме;
3) получить тригонометрическую форму числа 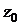 и вычислить с ее помощью
и вычислить с ее помощью 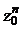 . Ответ записать в тригонометрической и в алгебраической формах.
. Ответ записать в тригонометрической и в алгебраической формах.
Решение задачи 1.
1) Найдем корни уравнения 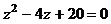 на множестве комплексных чисел:
на множестве комплексных чисел:
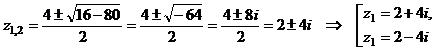
(здесь использовано: 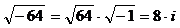 ).
).
2) Чтобы найти комплексное число 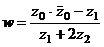 , вычислим сначала
, вычислим сначала 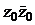 :
:
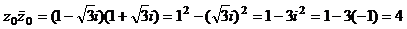 (
( 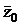 – это число, сопряженное числу
– это число, сопряженное числу 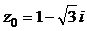 , т.е.
, т.е. 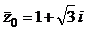 ).
).
Затем находим числитель 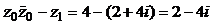 и знаменатель
и знаменатель 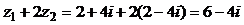 .
.
Теперь вычисляем w, используя домножение числителя и знаменателя на число, сопряженное знаменателю:
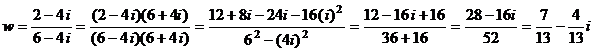
– получили число w в алгебраической форме.
3) Комплексное число 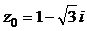 задано в алгебраической форме
задано в алгебраической форме 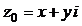 , где x = 1, y =
, где x = 1, y = 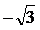 . Получим тригонометрическую форму этого числа
. Получим тригонометрическую форму этого числа
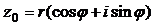 , используя формулы (13) и (14). Вычислим модуль комплексного числа
, используя формулы (13) и (14). Вычислим модуль комплексного числа 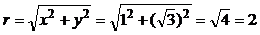 и его аргумент:
и его аргумент:
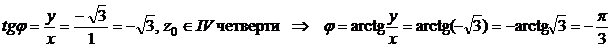
Таким образом, 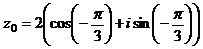 – тригонометрическая форма числа z0.
– тригонометрическая форма числа z0.
Для вычисления 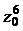 используем формулу (15) возведения комплексного числа в натуральную степень:
используем формулу (15) возведения комплексного числа в натуральную степень:
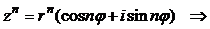
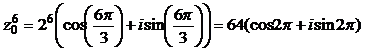 .
.
Здесь аргумент 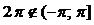 . Выбираем главное значение аргумента, принадлежащее промежутку
. Выбираем главное значение аргумента, принадлежащее промежутку 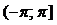 , используя формулу (11):
, используя формулу (11): 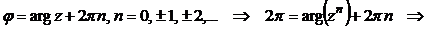 при n = – 1 получаем
при n = – 1 получаем 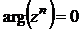 . Тригонометрическая форма комплексного числа
. Тригонометрическая форма комплексного числа 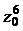 для
для 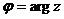 имеет вид:
имеет вид:
 .
.
Подставив значения cos0 = 1, sin0 = 0, получим алгебраическую форму этого числа: 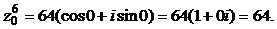
Ответы: 1) 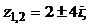 2)
2) 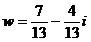 ; 3)
; 3) 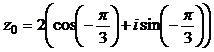 ;
;
 = 64.
= 64.
Задача 2. Дана функция комплексной переменной 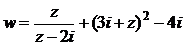 , где z = x + iy, и точка z0 = – 1 + 3i. Требуется:
, где z = x + iy, и точка z0 = – 1 + 3i. Требуется:
1) представить функцию в виде w = u(x,y) +iv(x,y), выделив ее действительную и мнимую части;
2) проверить, является ли функция w аналитической;
3) в случае аналитичности функции w найти ее производную w′ в точке z0.
Решение.
1) Выделим действительную и мнимую части функции:
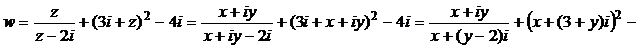
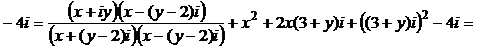
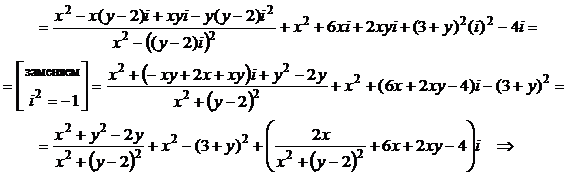
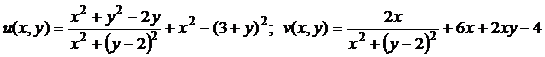 .
.
2) Чтобы установить аналитичность функции w, проверим выполнение условий Коши-Римана (10):
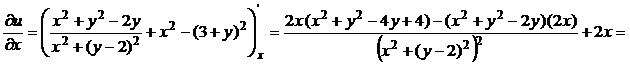
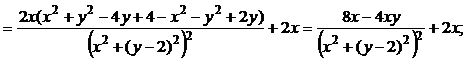
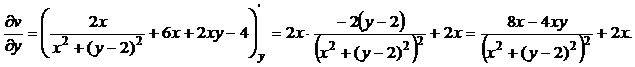
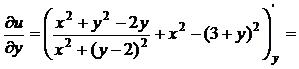
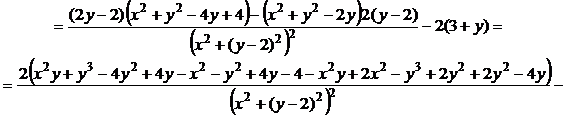
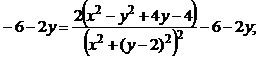
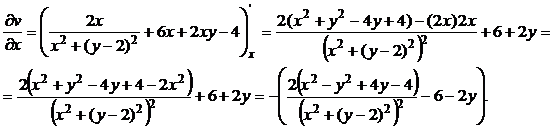
Получили: 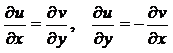 . Условия Коши-Римана выполняются во всех точках, кроме особой точки z = 2i, в которой функции x = 0, y = 2 и функции u(x, y) и v(x, y) не определены. Следовательно, функция
. Условия Коши-Римана выполняются во всех точках, кроме особой точки z = 2i, в которой функции x = 0, y = 2 и функции u(x, y) и v(x, y) не определены. Следовательно, функция 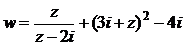 – аналитическая при
– аналитическая при 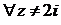 .
.
3) Найдем производную функции:
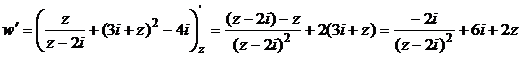 .
.
Вычислим значение производной функции в точке z0 = – 1 + 3i.

Ответы:
1) 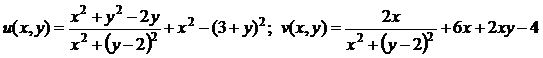 ;
;
2)функция 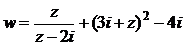 аналитическая при
аналитическая при 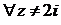 ;
;
3) 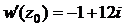 .
.
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. –М.: Айрис-пресс, 2003. – 288 с.
2. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 2 / Д.Т. Письменный. –М.: Айрис-пресс: Рольф, 2002. – 256 с.
3. Пискунов, Н.С. Дифференциальное и интегральное исчисление: учебник для втузов. В 2 т. Т. 1 / Н. С. Пискунов.– М.: Интеграл-Пресс, 2001.– 456 с.
4. Шипачев, В.С. Высшая математика: учебник для вузов / В.С. Шипачев.– М. : Высш. шк., 2007.– 479 с.
5. Данко, П.Е. Высшая математика в упражнениях и задачах: учебное пособие для втузов. В 2 ч. Ч.1 / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова.– М.: Оникс: Мир и образование, 2005.– 304 с.
6. Данко, П.Е. Высшая математика в упражнениях и задачах: учебное пособие для втузов. В 2 ч. Ч.2 / П. Е. Данко, А.Г. Попов, Т.Я. Кожевникова.– М.: Оникс: Мир и образование, 2005.– 416 с.
7. Шипачев, В.С. Задачник по высшей математике / В.С. Шипачев.– М. : Высш. шк., 2001.– 304 с.
8. Кручкович Г.И. Сборник задач и упражнений по специальным главам высшей математики: учебное пособие для втузов. / Г.И. Кручкович [и др.], под ред. Г.И. Кручковича. – М.: Высш. шк., 1970.– 512 с.
