Дифференциальные уравнения с разделяющимися переменными
Определение. Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно привести к виду у' = f(x)g(у).
Уравнения такого вида решаются с помощью разделения переменных 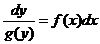
и интегрирования обеих частей полученного уравнения.
Замечание: при решении дифференциальных уравнений с разделяющимися переменными возможна потеря решений при разделении переменных
Пример 1. Решить уравнение хуу' + 1 = у.
Решение.
Разделим переменные: хуу' = у – 1,
ху 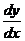 = у – 1.
= у – 1.
Последовательно разделив обе части уравнения на х(у – 1) и умножив на dx, получим уравнение
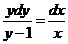 .
.
Проинтегрируем обе части уравнения
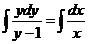 ;
;
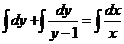 ;
;
у + ln|у – 1| = ln|х| + ln С;
у + ln|у – 1| = ln|Сх|
Так как при делении мы полагали, что х ≠ 0, а у ≠ 1, то могли «потерять» решения х = 0, у = 1.
Подставив их в данное уравнение имеем х = 0 не является решением данного уравнения, а у = 1 является его решением.
Ответ: у + ln|у – 1| = ln|Сх|, у = 1.
Уравнения вида у' = f(аx + ву), где а и в числа приводятся к уравнению с разделяющимися переменными заменой z = аx + ву, где переменная z считается функцией от х.
Пример 2. Решить уравнение у' – у = 3х +1.
Решение.
у' – у = 3х +1;
у' = 3х + у +1.
Положим z = 3х + у, тогда z' = у' + 3; у' = z' – 3.
Подставим данные значения в уравнение, будем иметь
z' – 3 = z + 1;
z' = z + 4;
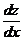 = z + 4;
= z + 4;
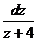 = dx.
= dx.
Проинтегрировав получаем ln|z + 4 | = х + С;
ln|3х + у + 4 | = х + С;
3х + у + 4 = ех + С;
у = ех –3х – 4+ С.
Ответ: у = ех –3х – 4+ С.
* *
*
231. Проверить, что данная функция является интегралом (решением) данного дифференциального уравнения:
а) у = 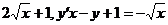 ; b) у = ; b) у = 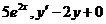 ; ; | с) у = 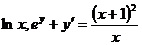 ; d) у = ; d) у = 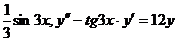 . . |
232. Проверить, что данная функция является интегралом данного дифференциального уравнения:
а) у = 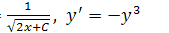 ;
;
b) у = 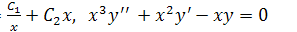 ;
;
с) у = 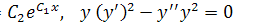 ;
;
d) у = 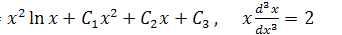 .
.
233. Составить дифференциальное уравнение, решением которого является функция:
а) у = 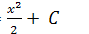 ; b) у = ; b) у = 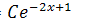 ; ; | с) у = 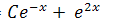 ; d) у = ; d) у = 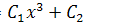 . . |
234. Решить уравнения с разделяющимися переменными:
| а) у’ = 2x + 1; | e) 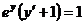 ; ; |
| b) у’ – y2 = 1; | f) 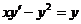 ; ; |
с) у’ 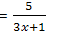 ; ; | g) 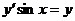 ; ; |
d) 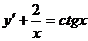 ; ; | h) 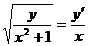 . . |
235. Решить уравнения с разделяющимися переменными:
а) 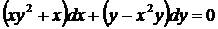 ;
;
b) 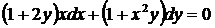 ;
;
с) 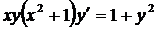 ;
;
d) 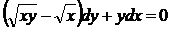 .
.
236. Решить задачу Коши:
а) у’ 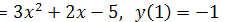 ;
;
b) у’ 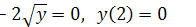 ;
;
с) у’ 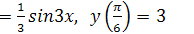
d) у’ 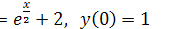 .
.
237. Составить дифференциальное уравнение процесса:
а) изменения скорости при замедленном прямолинейном движении тела под действием силы сопротивления среды, пропорциональной скорости υ;
b) радиоактивного распада вещества, если скорость распада пропорциональна массе т, нераспавшегося вещества;
с) увеличения числа микробов N в питательной среде, если число делящихся в единицу времени микробов пропорционально имеющемуся числу микробов;
d) изменения температуры тела Т в среде с температурой Т1, если скорость изменения Т пропорциональна разности температур тела и среды.
238. Процесс изменения величины описывается дифференциальным уравнением V 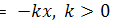 , где х – значение величины в момент времени t с. В начальный момент времени значение величины равнялось х, а через 10 с уменьшилось в два раза. Найдите зависимость величины от времени. Определите, во сколько раз изменилось значение величины через 100 с. Через какое время значение величины уменьшится в 100 раз?
, где х – значение величины в момент времени t с. В начальный момент времени значение величины равнялось х, а через 10 с уменьшилось в два раза. Найдите зависимость величины от времени. Определите, во сколько раз изменилось значение величины через 100 с. Через какое время значение величины уменьшится в 100 раз?
239. Скорость распада радия в каждый момент времени пропорциональна его наличной массе. Определите, какой процент массы т0 радия распадется через 200 лет, если известно, что период полураспада радия равен 1590 лет.
240. При брожении скорость прироста действующего фермента пропорциональна его имеющейся массе. Через 2 часа после начала брожения масса фермента составила 2 г, через 3 часа – 3 г. какова была первоначальная масса фермента?
МЕТОДИЧЕСКИЕ МАТЕРИАЛЫ ДЛЯ ОРГАНИЗАЦИИ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ
ТЕМАТИЧЕСКИЙ ПЛАН ДИСЦИПЛИНЫ Б2.Б.1 МАТЕМАТИКА
Направление подготовки: 44.03.02 Психолого-педагогическое образование
ОЧНАЯ ФОРМА ОБУЧЕНИЯ
| Всего зачётных единиц 3 Всего часов по учебному плану: 108 Ауд. (ЛК – 22ч., ПК 32ч., ЛР ______) Самост. 54 часа Зачет с оценкой | Трудоемкость | Аудиторные занятия | Самост. | Форма промежуточн.контроля | |||
| ЛК | ПК | ЛР | |||||
| № пп | Наименование разделов и тем | ||||||
| 1. | Элементы линейной алгебры | ||||||
| 2. | Аналитическая геометрия на плоскости | ||||||
| 3. | Введение в математический анализ | ||||||
| 4. | Дифференциальное исчисление | ||||||
| 5. | Интегральное исчисление | ||||||
| Итого в 1семестре | зачет с оценкой |
ЗАОЧНАЯ ФОРМА ОБУЧЕНИЯ
| Всего зачётных единиц 3 Всего часов по учебному плану: 108 Ауд. (ЛК – 8ч., ПК 10ч., ЛР ______) Самост. 90 часов Контрольная работа Зачет с оценкой | Трудоемкость | Аудиторные занятия | Самост. | Форма промежуточн.контроля | |||
| ЛК | ПК | ЛР | |||||
| № пп | Наименование разделов и тем | ||||||
| 1. | Элементы линейной алгебры | ||||||
| 2. | Аналитическая геометрия на плоскости | ||||||
| 3. | Введение в математический анализ | ||||||
| 4. | Дифференциальное исчисление | ||||||
| 5. | Интегральное исчисление | ||||||
| Итого в 1семестре | зачет с оценкой |
СОДЕРЖАНИЕ ДИСЦИПЛИНЫ
| № п/п | Наименование раздела дисциплины | Содержание раздела |
| Элементы линейной алгебры | Матрицы, операции над матрицами, транспонированные и обратные матрицы, матричная форма записи системы линейных уравнений. Решение систем линейных уравнений методом Гаусса. Определители, их свойства и вычисление. Решение систем линейных уравнений методом Крамера | |
| 2. | Аналитическая геометрия на плоскости | Метод координат на плоскости. Полярная система координат. Уравнения прямой на плоскости. Взаимное расположение прямых, угол между прямыми. Кривые второго порядка, их уравнения, геометрические свойства линий второго порядка. Признак распадения линий второго порядка. |
| 3. | Введение в математический анализ | Функции. Предел функции. Теоремы о существовании предела. 1-ый и 2-ой замечательные пределы. Эквивалентные бесконечно малые величины. Непрерывность функции. Классификация точек разрыва |
| 4. | Дифференциальное исчисление | Определение производной функции. Правила дифференцирования. Таблица производных. Уравнение касательной к плоской кривой. Условия возрастания и убывания функции. Экстремумы функции. Выпуклость графика функции. Точки перегиба. Наибольшее и наименьшее значения функции на отрезке. Асимптоты. Общая схема исследования функции и построение графика. Понятие дифференциала и его применение к приближенным вычислениям. |
| 5. | Интегральное исчисление | Первообразная функции и неопределенный интеграл. Таблица неопределенных интегралов. Интегрирование по частям и подстановкой. Определенный интеграл и его свойства. Вычисление определенного интеграла. Приложения определенных интегралов к вычислению площадей плоских фигур. Понятие дифференциального уравнения и его решения. Задача Коши. Уравнения с разделяющимися переменными и их решение. |
ОРГАНИЗАЦИЯ САМОСТОЯТЕЛЬНОЙ РАБОТЫ СТУДЕНТОВ ОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
1. График самостоятельной работы студентов очной формы обучения
| Форма оценочного средства | Номер недели | |||||||||||||||||
| Математический диктант | х | х | х | х | х | |||||||||||||
| Самостоятельная работа | х | х | х | х | ||||||||||||||
| Контрольная работа | х | |||||||||||||||||
| Тестирование письменное, компьютерное | х | |||||||||||||||||
| Работа со справочной литературой | х | х | х | х | х | |||||||||||||
| Индивидуальные домашние задания | х | х | х | х |
Виды самостоятельной работы студентов
| Номер раздела учебной дисциплины | Виды СРС | Всего часов |
| 1. | 1) Самостоятельное изучение темы «Ранг матрицы. Действия над матрицами. Обратная и транспонированная матрицы. Диагональная матрица». 2) Подготовка к практическим занятиям 3) Выполнение индивидуальных практических заданий 4) Подготовка к самостоятельной работе | |
| 2. | 1) Самостоятельное изучение темы «Простейшие задачи аналитической геометрии на плоскости». 2) Подготовка к математическому диктанту по теме «Простейшие задачи аналитической геометрии на плоскости». 3) Подготовка к математическому диктанту по теме «Линии первого порядка». 4) Подготовка к практическим занятиям 4) Выполнение индивидуальных практических заданий 4) Подготовка к самостоятельной работе | |
| 3. | 1) Самостоятельное изучение темы «Функции. Предел функции. Эквивалентные бесконечно малые величины» 2) Подготовка к практическим занятиям 3) Выполнение индивидуальных практических заданий 4) Подготовка к самостоятельной работе | |
| 4. | 1) Самостоятельное изучение темы «Условия возрастания и убывания функции. Максимум и минимум функции. Выпуклость графика функции. Точки перегиба. Наибольшее и наименьшее значения функции на отрезке. Асимптоты.» 2) Подготовка к практическим занятиям 3) Выполнение индивидуальных практических заданий 4) Подготовка к самостоятельной работе | |
| 5. | 1) Самостоятельное изучение темы «Первообразная функции и неопределенный интеграл. Таблица неопределенных интегралов». 2) Подготовка к практическим занятиям 3) Выполнение индивидуальных практических заданий 4) Подготовка к итоговой контрольной работе. | |
| Итого часов в семестре: |
УЧЕБНО-МЕТОДИЧЕСКОЕ И ИНФОРМАЦИОННОЕ ОБЕСПЕЧЕНИЕ ДИСЦИПЛИНЫ
Основная литература
1. Демидович Б.П., Кудрявцев В.А. Краткий курс высшей математики: учеб. пос. для вузов.- М.: Астрель, 2008
2. Письменный Д.Т. Конспект лекций по высшей математике: полный курс.- 9-е изд.- М.: Айрис-Пресс, 2009
3. Письменный Д.Т. Конспект лекций по высшей математике: в 2-х.-Ч.1-2: - М.: Айрис-Пресс, 2008
4. Письменный Д.Т. Конспект лекций по высшей математике: ч. 2: - М.: Айрис-Пресс, 2007
Дополнительная литература
1. Алексеева Г.Ю. Математика: учебно-методическое пособие с практикумом для студентов естественнонаучных специальностей педагогических институтов. Борисоглебск, 2011.
2. Баврин И.И., Матросов В.Л. Высшая математика: учеб. для вузов.- М.: Владос, 2002
3. Виноградов И.М. Элементы высшей математики: учеб. для вузов.- М.: Высшая школа, 1999
4. Высшая математика. Стандартные задачи с основами теории: учеб. пос. для вузов.- СПб: Лань, 2009
5. Данко П.Е. и др. Высшая математика в упражнениях и задачах: в 2-х ч.: учеб. пос. для вузов.- М.: ОНИКС 21 век; Мир и Образование, 2005
6. Запорожец Г.И. Руководство к решению задач по математическому анализу. –М.: Высшая школа. -1966.
7. Ильин В.А., Куркина А.В. Высшая математика: учеб. для вузов.- М.: проспект; Изд-во Моск. ун-та. 2004
8. Мироненко Е.С. Высшая математика: Методические указания и контрольные задания для студ.-заочн.: - М.: Высшая школа, 2000
9. Сборник задач по высшей математике. 1 курс: учеб. пос. для вузов/ К.Н. Лунгу, Д.Т. Письменный и др.- 6-е изд.- М.: Айрис-Пресс, 2007
10. Сборник задач по высшей математике. 2 курс: учеб. пос. для вузов/ К.Н. Лунгу, Д.Т. Письменный и др.- 6-е изд.- М.: Айрис-Пресс, 2007
11. Шипачев В.С. Высшая математика: учеб. для вузов.- М.: Высшая школа, 2002
12. Шипачев В.С. Задачник по высшей математике: учеб. пос. для вузов.- М.: Высшая школа, 2001
13. Шипачев В.С. Основы высшей математики: учеб. пос. для вузов.- М.: Высшая школа, 2001
Электронно-цифровые ресурсы
| № п/п | Ссылка на информационный ресурс | Наименование разработки в электронной форме | Доступность (открытый или локальный доступ) |
| http://edu-lib.net/matematika-2/dlya-studentov/demidovich-b-p-kratkiy-kurs-vyisshey-mate | Демидович Б. П. Краткий курс высшей математики: Учеб. пособие для вузов / Б. П. Демидович, В. А. Кудрявцев. — М.: ООО «Издательство Астрель»; ООО «Издательство ACT», 2001. — 656 с.: ил. | Открытый доступ | |
| http://edu-lib.net/ | Письменный Д.Т. Конспект лекций по высшей математике: полный курс.- 9-е изд.- М.: Айрис-Пресс, 2009 | Открытый доступ | |
| http://biblioclub.ru/index.php?page=search | Запорожец Г.И. Руководство к решению задач по математическому анализу. –М.: Высшая школа. -1966 | Открытый доступ | |
| http://edu-lib.net/ | Лунгу К. Н., Макаров Е. В. Высшая математика. Руководство к решению задач. Ч. 1. — 2-е изд., перераб. и доп. — М.: ФИЗМАТЛИТ, 2010. |
ПРИЛОЖЕНИЕ К ПОЛОЖЕНИЮ О БАЛЛЬНО-РЕЙТИНГОВОЙ СИСТЕМЕ ОЦЕНКИ УСПЕВАЕМОСТИ СТУДЕНТОВ ПО ДИСЦИПЛИНЕ Б2. Б.1 «МАТЕМАТИКА»
Направление подготовки 44.03.02 Психолого-педагогическое образование
Основные положения
Рейтинговая система основана на подсчете баллов, «заработанных» студентом в течение семестра.
За один семестр студент в сумме может получить максимально 100 баллов. В этом случае оценку «5» за экзамен или зачет он получает автоматически.
100 баллов студент также может набрать за работу в семестре + зачет: большую часть баллов он получает в течение семестра, меньшую часть – за зачет.
Система включает все виды учебной нагрузки студента (теоретический материал, практические навыки, реферат, доклад, индивидуальные задания, тестирование и т.п.).
Текущий контроль успеваемости (в результате которого набирается очередное количество баллов) осуществляется периодически, но не реже 2 раза в семестр.
2. Система ориентирована на дисциплины со сравнимыми теоретической и практической частями, заканчивающиеся сдачей экзамена
По результатам работы в семестре студент может получить автоматическую оценку 5, 4 или 3 и может не сдавать зачет. Если оценка его не удовлетворяет (4 или 3), он может сдать зачет, и, возможно, повысить свою оценку. Студент, не получивший автоматической оценки, обязан сдавать зачет. Если он не набрал минимального числа баллов в течение семестра (30), то не допускается к зачету.
| Баллы за семестр | Автоматическая оценка | Баллы за зачет | Общая сумма баллов | Итоговая оценка |
| 91-100 | отлично | – | 91-100 | |
| 80-90 | хорошо | 0-35 | 80-99 > 100 | |
| 60-79 | удовлетворительно | 0-35 | 65-80 81-99 > 100 | |
| 30-59 | неудовлетворительно | 0-35 | 65-80 81-99 | |
| < 30 | - | 0-35 | 60-65 < 60 |
· максимальное число баллов в течение семестра – 100;
· максимальное число баллов за зачет – 35;
· минимальное число баллов за семестр – 30;
· не получает зачет и не допускается к зачету тот, кто не набрал минимального числа баллов (30) в семестре. В этом случае студент получает дополнительное задание, выполнив которое, он может быть допущен к сдаче зачета.
Текущий контроль
| Лекции (9 лекций) | Посещение лекции 1 балл | Пропуск лекции: по неуважит. прич. – -1 б.; по уважит. прич. – 0 б. |
| Практических занятий (18 занятий) | Посещение практического занятия 1 балл | Пропуск пр. занятия по неуважит. прич. – -1 б.; по уважит. прич. – 0 б. |
| Максимальное число баллов |
3. Промежуточный контроль
| Выполнение домашних заданий (15 занятий) | За правильное выполнение менее 50% заданий 0,5 балла | За правильное выполнение не менее 50% заданий 1 балл | За правильное выполнение 90-100% заданий 2 балла |
| Написание математического диктанта | За правильное выполнение 50% заданий 0,5 балла | За правильное выполнение 75% заданий 1 балл | За правильное выполнение 90-100% заданий 2 балла |
| Выполнение самостоятельной работы | За правильное выполнение 50% заданий 1 балл | За правильное выполнение 75% заданий 2 балла | За правильное выполнение 90-100% заданий 4 балла |
| Выполнение контрольной работы | За правильное выполнение 50% заданий 1 балл | За правильное выполнение 75% заданий 3 балла | За правильное выполнение 90-100% заданий 5 баллов |
| Выполнение индивидуального задания | За правильное выполнение 50% заданий 0,5 балла | За правильное выполнение 75% заданий 1 балл | За правильное выполнение 90-100% заданий 2 балла |
| Бонусный балл (творческие задания) | - | За рефераты, доклады, выступления, активную работу на практическом занятии от 3 до 8 баллов | |
| Штрафы (опоздания) | Невыполнение домашнего задания - 1 балл | Сдача работ с опозданием - 0,5 балла | - |
| Максимальное число баллов (без бонусных) | 59 баллов |
Итоговое количество баллов за семестр (без бонусных) 94
4. Критерии оценки студента на зачете
| Характеристика ответа | Баллы | Оценка |
| Студент отлично ориентируется в теоретическом материале, умеет применять теоретические сведения для решения стандартных задач, задач повышенной сложности, задач на доказательство. | 30-35 | |
| Студент хорошо ориентируется в теоретическом материале, умеет применять теоретические сведения для решения стандартных задач и задач повышенной сложности. | 24-29 | |
| Студент может ориентироваться в теоретическом материале, имеет представление об основных методах решения задач, умеет применять теоретические сведения для решения типовых задач. | 20-23 |
ЗАДАНИЯ ПО МАТЕМАТИКЕ ДЛЯ СТУДЕНТОВ, ОБУЧАЮЩИХСЯ ПО ИНДИВИДУАЛЬНОМУ ПЛАНУ
Направление подготовки 44.03.02 Психолого-педагогическое образование
Форма отчетности – ЗАЧЕТ С ОЦЕНКОЙ
1. Изучить теоретическую литературу по разделу«Элементы линейной алгебры»:
· Матрицы. Операции над матрицами
· Определители. Свойства определителей. Вычисление определителей.
· Системы уравнений. Метод Гаусса. Метод Крамера.
2. Изучить теоретическую литературу по разделу«Элементы аналитической геометрии»:
· Простейшие задачи аналитической геометрии на плоскости.
· Линии первого порядка.
· Линии второго порядка (окружность, эллипс, гипербола, парабола, признак распадения линий второго порядка).
3. Изучить теоретическую литературу по разделу«Введение в математический анализ»:
· Понятие предела функции. Основные теоремы о пределе функции. Основные формулы
· Вычисление предела функции
4. Изучить теоретическую литературу по разделу«Дифференциальное исчисление»:
· Понятие производной. Свойства производной. Основные формулы вычисления производной. Механический и физический смысл производной
5. Изучить теоретическую литературу по разделу«Интегральное исчисление»
· Понятие интеграла. Свойства интегралов. Основные формулы вычисления интеграла. Формула Ньютона-Лейбница. Площадь плоской фигуры. Объем тела вращения
6. Изучить теоретическую литературу по разделу«Дифференциальные уравнения»:
· Понятие дифференциального уравнения. Решение уравнения. Задача Коши. Уравнение с разделяющимися переменными.
7. Знать определения основных понятий по данным разделам формулировки свойств и теорем.
8. Уметь иллюстрировать основные понятия примерами.
Из первого раздела пособия (стр. 7-84) решить задачи №№ 5(b), 11(а), 19(b), 24(а), 31, 42, 80, 102, 122, 137(а), 141(d), 144(а), 147(а), 165(а), 186(а), 202(а), 205(b), 209(b), 216(b), 220(а), 224(а), 234(а), 236(а).
ВОПРОСЫ К ЗАЧЕТУ С ОЦЕНКОЙ
Направление подготовки 44.03.02 Психолого-педагогическое образование
1.Матрицы и операции над ними.
2.Определители, свойства определителей. Вычисление определителей n-ного порядка.
3.Системы линейных уравнений. Решение систем линейных уравнений методом последовательного исключения неизвестных (метод Гаусса).
4.Исследование систем линейных уравнений с помощью определителей (метод Крамера).
5.Простейшие задачи аналитической геометрии на плоскости. Координаты.
6.Декартова и полярная системы координат. Связь между полярной и декартовой прямоугольными координатами.
7.Проекция отрезка, длина и полярный угол отрезка. Расстояние между двумя точками.
8.Деление отрезка в данном отношении. Деление отрезка пополам.
9.Условие, при котором заданные точки лежат на одной прямой. Площадь треугольника.
10.Понятие уравнения линии. Общее уравнение прямой. Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через две точки.
11.Условие параллельности и перпендикулярности двух прямых. Угол между двумя прямыми.
12.Уравнение прямой в отрезках. Нормальное уравнение прямой.
13.Уравнение прямой, проходящей через данную точку параллельно данной прямой; перпендикулярно данной прямой.
14.Взаимное расположение прямой и пары точек. Расстояние от точки до прямой.
15.Алгебраические линии и их порядок. Окружность. Нахождение центра и радиуса окружности.
16.Эллипс. Каноническое уравнение эллипса. Полуоси. Эксцентриситет. Директрисы эллипса.
17.Гипербола. Каноническое уравнение гиперболы. Фокальный радиус, основной прямоугольник гиперболы, эксцентриситет и директрисы гиперболы.
18.Парабола. Каноническое уравнение параболы, величина параметра, фокус, директриса параболы.
19.Основные понятия дифференциального исчисления. Предел функции. Простейшие пределы.
20.Непрерывность функции в точке.
21.Определение производной. Геометрический и физический смысл производной.
22.Производная суммы, произведения, частного. Производная степенной сложной функции. Производные тригонометрических функций.
23.Применение производной к исследованию функций.
24.Первообразная функции, основное свойство первообразной. Неопределённый интеграл. Свойства неопределённого интеграла.
25.Основные способы интегрирования. Интегрирование посредством разложения подынтегральной функции на слагаемые. Пример.
26.Основные способы интегрирования. Интегрирование посредством замены переменной. Пример.
27.Основные способы интегрирования. Интегрирование по частям. Пример.
28.Основные способы интегрирования. Интегрирование тригонометрических функций. Пример.
29.Основные способы интегрирования. Интегрирование функций, содержащих квадратный трехчлен. Пример.
30.Определённый интеграл. Простейшие свойства определённого интеграла. Формула Ньютона-Лейбница.
31.Площадь плоской фигуры. Примеры.
32.Механические и физические приложения определенного интеграла. Объём тела вращения.
33.Дифференциальное исчисление функций нескольких переменных. Частные производные, дифференцируемость функции в точке.
34.Полный дифференциал функции. Производные высших порядков.
35.Понятие дифференциального уравнения, дифференциальное уравнение первого порядка. Теорема о существовании и единственности решения дифференциального уравнения.
36.Дифференциальное уравнение с разделяющимися переменными.
ВНЕАУДИТОРНАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ ДЛЯ СТУДЕНТОВ ЗАОЧНОЙ ФОРМЫ ОБУЧЕНИЯ
Направление подготовки 44.03.02 Психолого-педагогическое образование
МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ВЫПОЛНЕНИЮ И ОФОРМЛЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ
Цель контрольных работ – закрепить и проверить знания, полученные студентами в процессе самостоятельного изучения учебного материала, а также выявить умение применять полученные теоретические знания при решении конкретных математических задач.
Студент должен выполнить в установленные сроки контрольные работы.
Задания к контрольным работам распределены по десяти вариантам.
Вариант контрольной работы совпадает с последней цифрой зачетной книжки или студенческого билета.
Прежде чем приступить к выполнению контрольной работы, необходимо изучить соответствующие разделы курса по рекомендуемой литературе и разобрать примеры решения подобных задач, приведенные в данном пособии.
При выполнении контрольных работ необходимо руководствоваться следующими требованиями:
Контрольная работа должна быть оформлена в тетради в клеточку (достаточно 12 листов).
Титульный лист работы оформляется согласно образцу.
Каждое задание желательно начинать с новой страницы (оставляя место для работы над ошибками).
Решение задач необходимо приводить по порядку от первого к десятому заданию.
Перед решением задачи следует привести её полное условие.
Решение задач нужно сопровождать формулами, развернутыми расчетами, выводами.
Задачи, по которым даются ответы без развернутых расчетов, пояснений, выводов, считаются нерешенными.
Контрольная работа должна быть оформлена аккуратно, написана от руки разборчиво без помарок, без сокращений слов (кроме общепринятых сокращений).
Если по контрольной работе рецензентом сделаны замечания, студент должен учесть их и, не переписывая работы, внести необходимые исправления и дополнения.
Без выполненной контрольной работы студент не допускается к итоговому зачету.
ОБРАЗЕЦ ОФОРМЛЕНИЯ ТИТУЛЬНОГО ЛИСТА КОНТРОЛЬНОЙ РАБОТЫ

СОДЕРЖАНИЕ КОНТРОЛЬНОЙ РАБОТЫ С ПРИМЕРАМИ ВЫПОЛНЕНИЯ ЗАДАНИЙ
ЗАДАНИЕ 1.
Вычислить определитель третьего порядка.
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ:
Вычислить определитель третьего порядка

 -1 2 -3
-1 2 -3
4 -5 6 .
7 8 -9
Решение.

 -1 2 -3
-1 2 -3
Δ =4 -5 6 = -1 ∙ (-5) ∙ (-9) + 2 ∙ 6 ∙ 7 + (-3) ∙ 4 ∙ 8-
7 8 -9 -(-3) ∙ (-5) ∙ 7 – 2 ∙ 4 ∙ (-9) –(-1) ∙ 6 ∙ 8 =
= -45 + 84 – 96 – 105 + 72 + 48 = 204 – 246 = - 42.
Ответ: Δ = - 42.
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
| вариант | задание | вариант | задание |
| В. 1. | 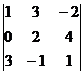 | В. 6. | 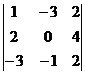 |
| В. 2. | 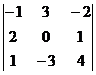 | В. 7. | 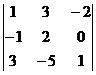 |
| В. 3. | 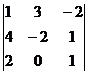 | В. 8. | 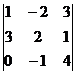 |
| В. 4. | 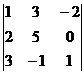 | В. 9. | 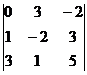 |
| В. 5. | 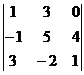 | В. 10. | 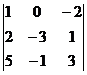 |
ЗАДАНИЕ 2.
Решить систему уравнений методом последовательного исключения неизвестных в матричной форме.
ПРИМЕР РЕШЕНИЯ ЗАДАЧИ:
х1 - 3 х2 + 2х3 – х4 = -7,
- х1 + 2х2 – х3 + 3х4 = 9,
2х1 + х2 – 3х3 – х4 = 2,
-3х1 + х3 + х4 = 1.
Решение.
Составим расширенную матрицу системы и приведем ее к диагональной форме:
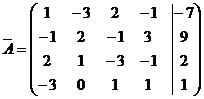 ~
~ 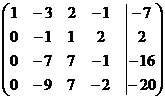 ~
~ 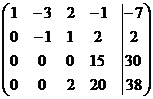 ~
~
~ 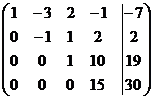
Восстановим систему уравнений:
х1 – 3х2 + 2х3 – х4 = -7,
- х2 + х3 + 2х4 = 2,
х3 +10 х4 = 19,
15 х4 = 30.
Из последней системы находим: х4 = 2; х3 = -1; х2 = 1; х1 = 0.
Ответ: {(0,1,-1,2)}
ЗАДАНИЯ ДЛЯ САМОСТОЯТЕЛЬНОГО РЕШЕНИЯ
| вариант | задание | вариант | задание |
| В. 1. | х1 - 3 х2 + 2х3 – х4 = -3, -2х1 + 2х2 – х3 + 3х4 = 5, -х1 + х2 – х3 – 2х4 = -4, 3х1 + х3 + 2х4 = 6. | В. 6. | 3х1 - х2 + 2х3 – х4 = -3, - х1 + 2х2 – х3 + 3х4 = 6, 2х1 + х2 – 3х3 – х4 = 3, -3х1 + х2 + х4 = 1. |
| В. 2. | х1 - 2 х2 + х3 – 3х4 = -6, -х1 + х2 –5 х3 + х4 = -2, -3х1 + х2 – х3 – 2х4 = -2, 2х1 + 3х3 + х4 = 3. | В. 7. | -х1 + х2 + 2х3 – х4 = -1, 2х1 + 2х2 – х3 + 3х4 = 3, -х1 + х2 – х3 – 2х4 = -4, х1 – х2 + 2х4 = 1. |
| В. 3. | х1 - 3 х2 + 2х3 –5 х4 = -3, -3х1 + х2 – 2х3 + х4 = -3, -х1 + 3х2 – х3 – 7х4 = 2, 2х1 - х3 + 3х4 = 5. | В. 8. | х1 - 2 х2 + 3х3 – х4 = -3, 2х1 + 2х2 – х3 + 5х4 = 7, -х1 + х2 – 3 х3 – 2х4 = 2, 3х1 + х3 + 7х4 = 5. |
| В. 4. | 2х1 - 3 х2 + х3 – х4 = -3, х1 + 2х2 – 7х3 + 3х4 = 2, -х1 + х2 – х3 – 2х4 = 3, 3х1 + 5 х3 + 2х4 = 1. | В. 9. | х1 - 3 х2 + 2х3 – х4 = -4, -х1 + 2х2 – х3 + 3х4 = 0, -2х1 + х2 – 5х3 – 2х4 = 2, -3х1 + х2 + 2х4 = -3. |
| В. 5. | х1 - 2 х2 – 3х3 + х4 = 2, -2х1 + 2х2 – х3 + 3х4 = 6, -3х1 + х2 – х3 – 2х4 = 0, х1 + х3 + 2х4 = 1. | В. 10. | х1 - 3 х2 + 2х3 – х4 = -6, -х1 + 3х2 – х3 + 2х4 = 6, 2х1 + х2 – х3 – 2х4 = 0, -3х2 + х3 + 2х4 = -2. |
