Эйлеровы (четные) графы. Цикломатическое число

Здесь мы будем рассматривать подграфы, может быть, несвязные, содержащие все вершины графа. Пусть G - граф, содержащий p занумерованных ребер е₁, е₂..., ер. Каждому подграфу H Í G поставим в соответствие p-мерный вектор H = (a₁, а₂..., ар) (обозначение
вектора – такое же, как подграфа) из нулей и единиц: ai= 1, если eiÎ Н; ai= 0, если eiÏ H,
т.е. характеристический вектор подграфа Н. Это соответствие, очевидно, взаимно однозначное. Более того, сумме по модулю 2 (симметрической разности) Н₁Δ Н₂подграфов Н₁и Н₂– соответ-ствует (поразрядная) сумма по модулю 2 их характеристических векторов Н₁Å Н₂. Над множе-ством коэффициентов {0, 1} множество всех подграфов образует линейное пространство: умножение любого подграфа Н на 1 дает Н, умножение на 0 - пустой подграф, т.е. подграф, не содержащий ребер и состоящий из одних изолированных вершин графа G. Нетрудно видеть, что линейное пространство подграфов графа G и линейное пространство характеристических векторов его подграфов изоморфны и имеют размерность p. Базисом может служить множество всех однореберных подграфов. Характеристический вектор каждого такого подграфа содержит ровно одну единицу, причем для разных подграфов - на разных местах. Поэтому в виде суммы таких подграфов можно представить любой подграф графа G.

Назовем граф четным, если степени всех его вершин - четные числа. Любую элементарную цепь (кроме цикла) в четном графе можно продлить ребром, не принадлежащим цепи, так как конец цепи имеет степень 1 в цепи и степень не меньше 2 в графе. Если граф конечен, то, продолжая цепь, мы через конечное число шагов вторично придем в уже пройденную вершину, т.е. часть полученной (уже не элементарной) цепи образует элементарный цикл, после удаления которого остается четный граф, так как все степени изменяются на четное число (2 - для вершин цикла и 0 - для вершин, не принадлежащих циклу). В этом графе можно снова выделить некоторый элементарный цикл и т.д., пока в графе не останется ни одного ребра. Таким образом, каждый конечный четный граф можно представить в виде суммы попарно не пересекающихся (по ребрам) элементарных циклов, откуда, в частности, следует, что каждое его ребро циклическое.

Если конечный четный граф связен, то нетрудно показать (например, индукцией по числу его элементарных циклов), что в нем существует простой (т.е. не самопересекающийся по ребрам) цикл, содержащий все ребра графа. Такой цикл называется эйлеровым циклом, а обладающий им граф называется эйлеровым графом. Поскольку каждая вершина простого цикла имеет в нем четную степень (каждое прохождение через вершину по циклу использует два ребра, инцидентных этой вершине), то справедлива теорема Эйлера ‑ для того чтобы конечный связный граф был эйлеровым, необходимо и достаточно, чтобы он был четным. В конечном несвязном четном графе все компоненты связности - эйлеровы графы.

Будем называть вершину ориентированного графа равновесной, если число дуг, входящих в вершину, равно числу дуг, исходящих из нее. Ориентированный граф назовем равновесным, если все его вершины равновесные.

Обход (неориентированного) эйлерова графа по эйлерову циклу ориентирует каждое ребро графа в направлении обхода. Ясно, что при такой ориентации эйлеров граф является равновесным (по одной дуге входим в вершину, по другой выходим; соответствие - взаимно однозначное). Пусть теперь дан равновесный граф. Повторяя предыдущее рассуждение (вместо циклов надо говорить о контурах), легко показать, что каждый конечный равновесный граф можно представить в виде суммы элементарных контуров, попарно не пересекающихся по ребрам (а также то, что в конечном связном равновесном графе существует простой контур, содержащий все ребра графа).

Другими словами, теорема Эйлера означает, что четность всех вершин графа есть необходимое и достаточное условие существования обхода графа (с возвращением в начало обхода), при котором каждое ребро проходится ровно один раз.

Из теоремы Эйлера можно вывести интересное следствие. В произвольном связном графе G раздвоим каждое ребро е = (v₁, v₂), т.е. заменим его парой кратных ребер е¢, е″ с теми же вершинами. Степень каждой вершины удвоится и станет четной. В полученном четном графе G⁽²⁾ существует эйлеров цикл (а если ребра е¢, е″ ориентировать в противоположных направлениях, то каждая вершина будет равновесной, и существует эйлеров контур). Если рассмотреть его как обход графа G⁽²⁾, снова склеить пары е¢, е″ в одно ребро, то в первоначальном графе G эта траектория будет (уже не простым) циклом, проходящим через каждое свое ребро ровно два раза в противоположных направлениях. Итак, в каждом связном графе существует цикл, содержащий каждое ребро графа ровно 2 раза, что можно трактовать как соответствующий обход лабиринта с возвращением в начало обхода (для графа на рис. 2.17 указан порядок обхода).

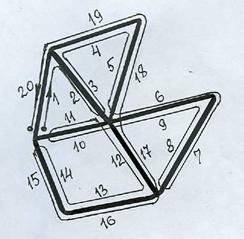
Рис. 2.17

Элементарный путь, проходящий через все вершины графа по одному разу, называется гамильтоновым; если совпадают его начало и конец, то это гамильтонов цикл.

Известная задача о коммивояжере формулируется так: имеется n городов, попарные расстояния между которыми заданы. Коммивояжер желает посетить все города так, чтобы суммарная длина пути была минимальной. Это означает, что нужно найти гамильтонов путь минимальной длины в полном графе Кn, ребрам которого приписаны положительные числа - длины ребер (для варианта задачи - обхода с возвращением в начало пути - ищется минимальный гамильтонов цикл).

Последовательность перестановок, описанная в п. 1.3, может быть интерпретирована следующим образом. Рассмотрим граф Gn, вершины которого соответствуют всем n! перестановкам множества {1, 2,..., n}, а ребра связывают пары вершин, отличающиеся транспозицией соседних элементов (таким образом, каждая вершина соединена с (n - 1) другими вершинами). Тогда указанная последовательность соответствует гамильтонову пути в графе Gn. На рис. 2.18, а,б - соответствующие иллюстрации для n = 3 и n = 4.

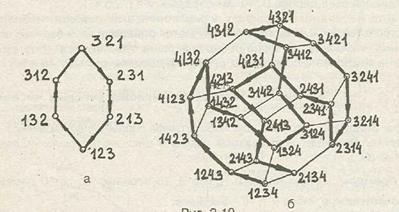
Рис 2.18

Сумма (симметрическая разность) двух четных подграфов любого графа есть также четный подграф. Если s₁и s₂- степени некоторой вершины а в подграфах H₁и H₂соответственно,
а s₁₂- ее степень в пересечении H₁∩ H₂, то степень s(a) вершины a в подграфе Н₁Å Н₂равна
(s₁- s₁₂) + (s₂- s₁₂) = s₁+ s₂- 2s₁₂(кстати, это пример применения комбинаторной формулы включения-исключения). Если s₁и s₂- четные, то s(a) также четное. Поэтому четные подграфы образуют подпространство в линейном пространстве всех подграфов, которое совпадает с подпространством, натянутым на множество всех элементарных циклов.

Перейдем к выяснению размерности ν(G) этого подпространства. Пусть G - связный граф с p ребрами и b вершинами, D - некоторый его остов. Число ребер остова равно (b-1), - поэтому число хорд равно (p - b + 1). Каждая хорда (α, β) вместе с единственной элементарной цепью
[α, β] Í D образует элементарный цикл. Векторы всех таких циклов (для разных хорд) образуют независимую систему å, так как каждый из циклов содержит ребро (свою хорду), не принадлежащее ни одному из остальных циклов системы. Отсюда ν(G) ³ p - b + 1.

С другой стороны, каждый четный подграф, в частности любой простой цикл выражается через циклы системы å. Действительно, прибавим к четному подграфу Н те циклы из å, кото-рые содержат хорды графа, принадлежащие Н. Полученная сумма не будет содержать ни одной хорды (каждая хорда входит в сумму дважды: в подграф Н и в один из циклов системы å),
т.е. будет некоторым подграфом дерева D, откуда следует, что это пустой подграф, так как в противном случае четный подграф (сумма Н и циклов), имеющий элементарные циклы, содержался бы в дереве D. Таким образом, ν(G) = p - b + 1.

Для несвязного графа с k компонентами связности базис пространства четных подграфов получается объединением базисов его связных компонент, а число ребер и вершин суммируется. Поэтому, если i-я компонента содержит piребер и biвершин, то ν = p - b + k, где p = ,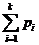
b = 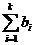. Число ν(G) называется цикломатическим числом графа. Ввиду того, что ν ≥ 0, для любого графа справедливо неравенство p + k ≥ b. Деревья - это связные графы с цикломатическим числом, равным 0.

Примеры. 1. Для полного графа К₅(5 вершин, 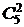= 10 ребер) цикломатическое число
ν(К₅) = 10 - 5 + 1 = 6.

2. Для графа на рис. 2.11 имеем: p = 18, b = 11, k = 1, откуда ν(G) = 18 - 11 + 1 = 8.

3. Рассмотрим соотнесенный неориентированный граф для графа на рис. 2.18, б. Число его вершин равно числу перестановок из 4 элементов: 4! = 24. Степени всех вершин равны 3. Поэтому число ребер графа р = 24 · 3 / 2 = 36. Граф связен, т.е. k = 1. Цикломатическое число равно
ν(G) = 36 - 24 + 1 = 13.