Простые и эйлеровы циклы и графы. Задача о кенигсбергских мостах. Теорема Эйлера. Понятие дерева. Свойства деревьев. Остов графа.

Задача о кенигсбергских мостах.

Расположение мостов в г. Кенигсберге во времена Эйлера:

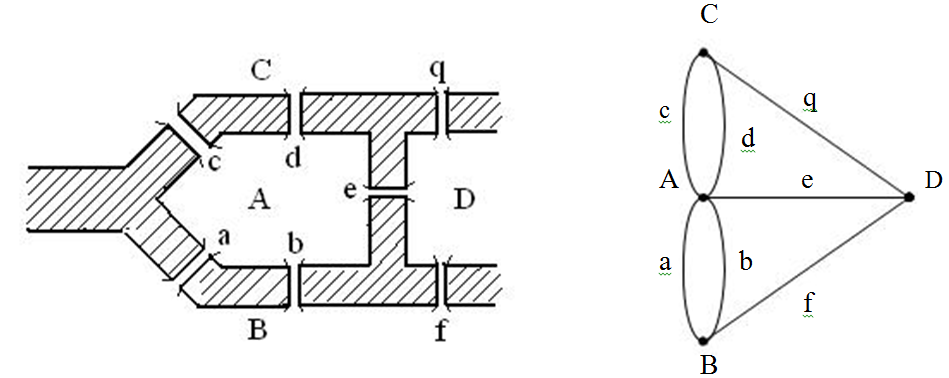
Требуется пройти каждый мост по одному разу и вернуться в исходную часть города. Так как в конце обхода нужно вернуться в исходную часть города и на каждом мосту побывать только по одному разу, то этот маршрут является простым циклом, содержащим все рёбра.

Опр.3. Простые циклы, содержащие все рёбра графа, называются эйлеровыми циклами, а графы, имеющие эйлеровы циклы – эйлеровыми графами.

Эйлеров цикл можно считать следом пера, вычерчивающего этот граф, не отрываясь от бумаги.

Условия, при которых граф будет Эйлеров.

Опр.3. G - неориентированный граф. Цикломатическим числом графа G называется Gpqk , где p - число связанных компонент, q - число

рёбер, k - число вершин.

Опр.4. Граф G называется связанным, если все его вершины связаны между собой рёбрами. Количество pv рёбер, инцидентных вершине vG

называется её степенью.

Теорема (Эйлера). Конечный неориентированный граф G тогда и только тогда Эйлеров, когда он связан и степени всех его вершин чётны.

Док-во. Пусть G - Эйлеров граф, т.е. все его циклы простые и содержат

все рёбра графа. Если существует цикл, проходящий через каждую дугу графа G точно один раз, то G , очевидно, связан. Каждый раз, когда цикл проходит через некоторую точку, мы приходим в эту точку по одной дуге, а выходим по другой. Следовательно, степени вершин чётны.

Пусть v - произвольная вершина на чётной степени графа G . Добавляя

к нему ребро, приходим к другой вершине. При этом степень этой вершины станет нечётной. При выходе из неё снова станет чётной. Исходная вершина станет чётной только после возвращения к исходной вершине. В результате получим связанную часть P графа G с чётными вершинами. Пусть v - общая вершина для P и G \ P . Построим в G \ P аналогичный цикл P, заканчивающийся в v.

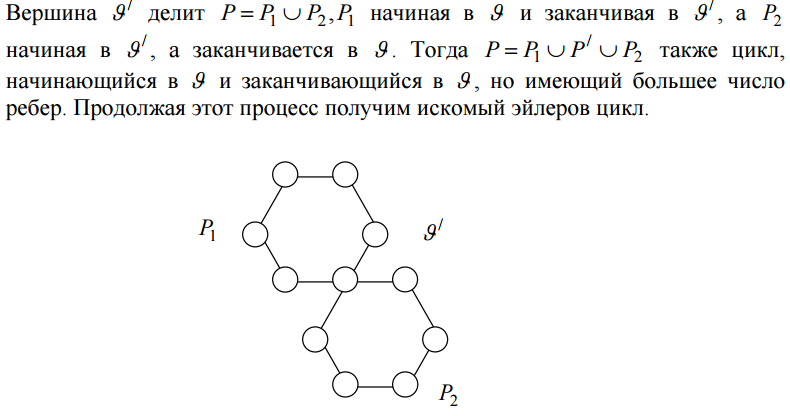
Замечание. В графе задачи о мостах, все вершины имеют нечетную степень. Следовательно, ее решение отрицательно.

Опр. 1. Деревом называется связанный грай, не содержащий на одного цикла. Дерево ориентированное, если его ребра ориентированы. Основные свойства.

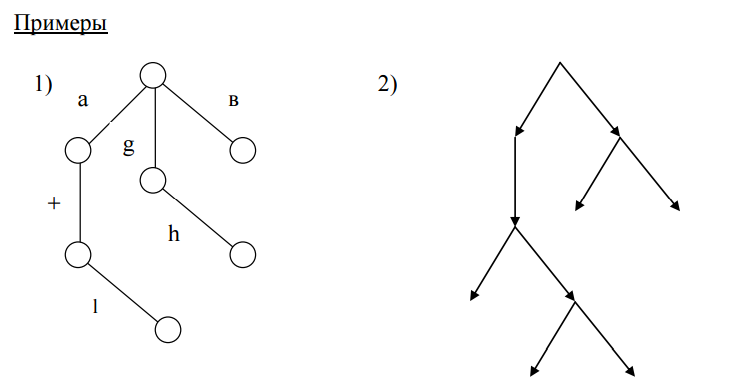
1) Любые две вершины дерева связаны одной и только одной цепью.

2) Если конечное дерево состоит более чем из одной вершины, оно имеет хотя бы две концевые вершины и хотя бы одно концевой ребро.

3) К каждую вершину ориентированного дерева (за исключением корня) входит только одно ребро.

4) Любое дерево можно ориентировать, выбрав в качестве корня (отмеченная вершина) любую его вершину. Следовательно, в конечном дереве число вершин на единицу больше числа ребер.

Опр. 2. Цикломатическим числом конечного не ориентированного, графа G называется число

 (G) _c_e_1

Где _c - число связанных компонентов (связанных подграфов);

n_e - число ребер;

n _ - число вершин.

5) Цикломатическое число дерева равно нулю

Опр.3. Плоскую геометрическую реализацию дерева, в которой ребра представляют отрезки прямых, а корнем являются – выделенная вершина, будем называть укладкой дерева.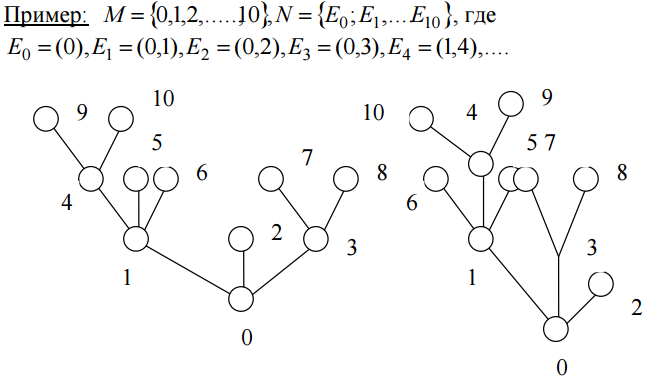

Две укладки одного дерева одинаковы, если порядки следования, исходящих ребер для соответствующих вершин совпадают.

Обозначим  (h) - максимальное число попарно неизоморфных деревьев с h ребрами, а ^* (h) - число укладок деревьев из соответствующего множества.