Эйлеровы и гамильтоновы графы

Определение.Пусть 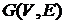– неориентированный граф. Цикл, который включает все ребра и вершины графа 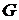, называется эйлеровым циклом. Граф имеющий эйлеров цикл, называется эйлеровым.

Теорема Эйлера. Конечный граф с более чем одной вершиной имеет эйлеров цикл тогда и только тогда, когда он связанный и каждая его вершина имеет четную степень. Следствие. Связанный граф 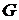является эйлеровым тогда и только тогда, когда семейство его ребер можно разбить на непересекающиеся по ребрам циклы.

Определение. Простой связанный граф 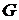называется гамильтоновым, если в нем существует цикл, проходящий через все его вершины.

Пример. На рис. 29 графы не являются гамильтоновыми, а граф – гамильтонов граф.

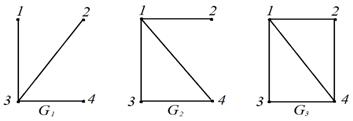
Рис. 29. Гамильтоновы и не гамильтоновы графы

Алгоритм выделения эйлерова цикла в связном мультиграфе с четными степенями вершин:

1. Выделим из 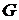цикл 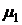(так как степени вершин четны, то висячие вершины отсутствуют). Положим .

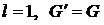2. Удаляем из 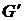ребра, принадлежащие выделенному циклу 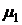. Полученный псевдограф снова обозначаем как 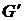. Если в 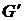отсутствуют ребра, то переходим к шагу 4. Если ребра есть, то выделяем из 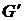цикл 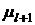и переходим к шагу 3.

3. Присваиваем 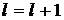и переходим к шагу 2.

4. По построению выделенные циклы содержат все ребра по одному разу. Если 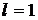, то искомый Эйлеров цикл найден (конец работы алгоритма). В противном случае находим циклы, содержащие хотя бы по одной общей вершине (в силу связности графа это всегда можно сделать). Склеиваем эти циклы. Повторяем эти операции, пока не останется один цикл, который является искомым.

Пример.Найдем эйлерову цепь в неориентированном графе 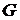, изображенном на рис. 30. Прежде, чем приступать к нахождению эйлеровой цепи, необходимо проверить степени вершин графа 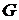, для существования эйлеровой цепи, необходимо и достаточно, чтобы в графе 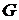ровно 2 вершины нечетной степени.

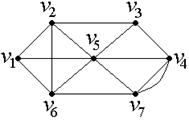
Рис. 30

В рассматриваемом графе нечетные степени имеют вершины 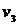и 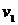(степень этих вершин равна 3). Соединяя эти вершины фиктивным ребром так, как показано на рис. 31, получаем граф :

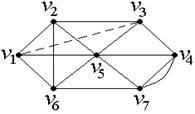
Рис. 31

Поскольку в конечном итоге будет получена цепь, то очевидно, что началом и концом этой цепи будут вершины с нечетными степенями. Поэтому, следуя описанному выше алгоритму, будем циклы 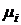так, чтобы хотя бы один из них начинался или кончался на вершинах 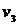или .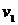

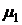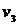
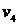
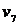
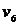
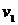
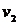
Пусть цикл составят ребра, проходящие через следующие вершины: 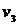. Согласно алгоритму, удаляем из 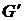все ребра, задействованные в цикле 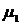. Теперь граф 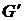будет таким, как показано на рис. 32.

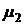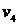
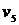
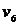
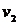
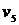
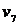
Составляем следующий цикл : 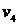. Граф 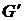после удаления ребер, составляющих цикл 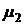, изображен на рис. 33.

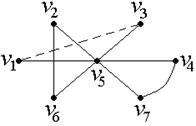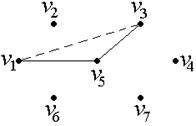Рис. 32	Рис. 33

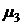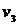
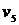
Очевидно, что последний цикл будет состоять из 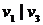, где последнее ребро, соединяющее вершины 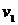и 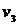– фиктивно. После удаления ребер, составляющих цикл 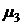, в графе 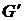не останется ни одного ребра.

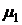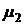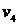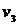
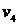
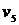
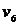
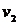
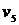
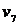
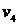
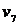
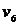
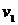
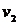
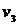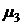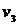
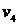
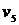
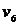
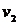
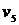
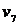
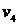
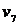
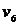
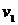
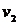
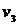
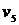
Теперь по общим вершинам склеиваем полученные циклы. Поскольку и имеют общую вершину , то, объединяя их, получим следующий цикл: . Теперь склеим получившийся цикл с циклом : 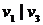. Удаляя фиктивное ребро, получаем искомую эйлерову цепь:

.

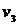
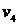
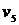
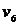
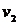
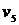
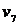
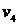
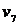
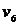
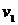
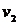
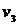
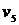
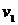7.8. Деревья. Основные определения

Неориентированным деревом(или просто деревом) называется связный граф без циклов. Этому определению эквивалентны, следующие определения:

а) дерево есть связный граф, содержащий 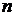вершин и 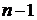ребер;

б) дерево есть граф, любые две вершины которого можно соединить простой цепью.

Пример. Графы, изображенные на рис. 34, являются деревьями.

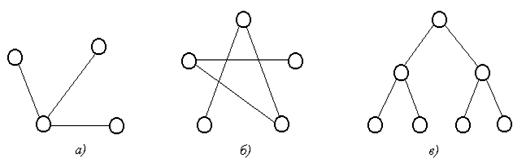
Рис. 34

Если граф несвязный и не имеет циклов, то каждая его связная компонента будет деревом. Такой граф называется лесом.

Остовным деревомсвязного графа 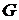называется любой его подграф, содержащий все вершины графа 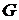и являющийся деревом.

Пример. Для графа, изображенного на рис. 35а), графы на рис. 35б) и 35в) являются остовными деревьями.

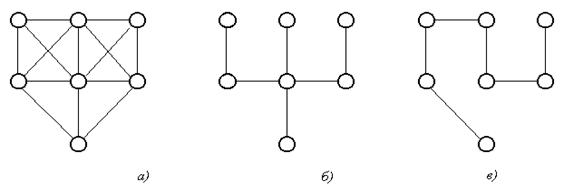
Рис. 35

Пусть граф 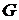имеет n вершин и 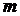ребер. Так как всякое дерево с 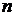вершинами по определению имеет 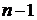ребер, то любое остовное дерево графа 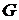получается из этого графа в результате удаления 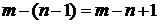ребер. Число 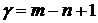называется цикломатическим числомграфа.