Теоремы сложения вероятностей

Пусть даны два события и требуется определить вероятность появления хотя бы одного из этих событий.

Теорема 4. Если события и несовместные, то вероятность появления одного из этих событий (сумма) равна сумме вероятностей данных событий, т.е.

.

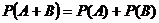Следствия:

Вероятность суммы нескольких несовместных событий 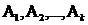равна сумме вероятностей этих событий, т. е.

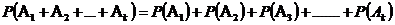
Если события 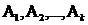образуют полную группу событий, то сумма их вероятностей равна единице.

Сумма вероятностей двух противоположных событий равна единице.

Теорема 5.Если события и совместные, то вероятность появления хотя бы одного из этих событий (сумма) равна сумме вероятностей этих событий без вероятности их совместного появления, т. е.

.

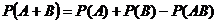Вероятность появления хотя бы одного события

В некоторых случаях вероятность события удобнее подсчитывать как вероятность противоположного другому событию.

Пусть события 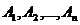попарно независимы и их вероятности известны и равны соответственно 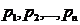, тогда вероятности противоположных им событий 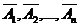будут равны .

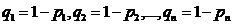Теорема 6. Вероятность появления хотя бы одного из попарно независимых событий 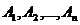равна разности между единицей и произведением вероятностей противоположных событий 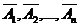, т.е.

.

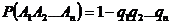Формула полной вероятности

Теорема.Если событие может наступить только при условии появления одного из несовместных событий 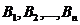, которые образуют полную группу, то вероятность события равна сумме произведений каждого из этих событий на соответствующие условные вероятности события , т. е.

.

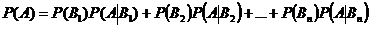Поскольку заранее не известно, какие из событий 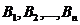наступят, то их называют гипотезами.

Вероятность гипотез. Формула Байеса

Часто, приступая к анализу вероятностей, мы имеем предварительные значения вероятностей, интересующих нас событий. После проведения испытания эти вероятности могут несколько уточняться.

Пусть произведено испытание, в результате которого появилось событие . Необходимо найти вероятности гипотез 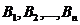, после того как испытание произведено, т. е. условные вероятности гипотез .

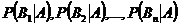Найдем сначала условную вероятность .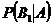

По теореме умножения .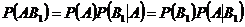

Отсюда .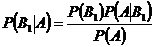

Аналогично выводятся формулы остальных гипотез.

В общем случае условная вероятность любой гипотезы 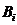, где 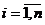, определяется как .

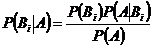Последняя формула называется формулой Байеса. Она позволяет переоценивать вероятности гипотез после того, как становится известным результат испытания, в итоге которого появилось событие .

14.

Пусть проводится 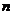независимых испытаний, в каждом из которых возможно только два исхода: либо событие появится, либо нет.

Условимся считать, что вероятность события в каждом испытании одна и та же и равна .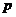

Тогда вероятность ненаступления события в каждом испытании так же постоянна и равна .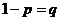

Формула Бернулли

О. 1.Если проводится несколько испытаний, причем вероятность появления события в каждом испытании не зависит от исходов других испытаний, то такие испытания называют независимымиотносительно события .

Теорема 1. Если вероятность 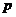наступления события в каждом из независимых испытаний постоянна, то вероятность 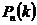того, что в 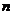независимых испытаниях событие появится ровно 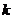раз, вычисляется по формуле

.
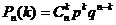