Разложение многочлена на множители

1.Вынесение множителя за скобку. Из распределительного закона непосредственно следует, что ac + bc = c ( a + b ). Этим можно воспользоваться для вынесения множителя за скобки.

2. Использование формул сокращённого умножения. Формулы сокращённого умножения позволяют довольно эффективно представлять многочлен в форме произведения.

3. Способ группировки

Рациональные функции.Разложение на сумму простейших дробей.Методы нахождения коэфф. Разложения

Рациональная функция — это дробь, числителем и знаменателем которой являются многочлены. Она имеет вид

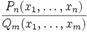
где 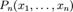, 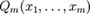— многочлены от любого числа переменных.

Частным случаем являются рациональные функции одного переменного:

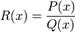, где P(x) и Q(x) — многочлены.

Свойства

§ Любое выражение, которое можно получить из переменных 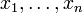с помощью четырёх арифметических действий, является рациональной функцией.

§ Множество рациональных функций замкнуто относительно арифметических действий и операции композиции.

§ Любая рациональная функция может быть представлена в виде суммы простейших дробей (см. Метод неопределённых коэффициентов), это применяется при аналитическом интегрировании.

Простейшими рациональными дробями являются рациональные дроби:

1)

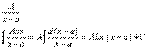
2)

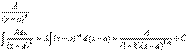
3)

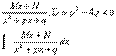
Выделяем полный квадрат и делаем замену переменной:

Тогда интеграл примет вид:

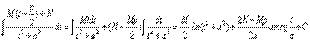
Делаем обратную замену переменной и получаем окончательный ответ.

Разложение правильной рациональной дроби на сумму простейших дробей.

Матрицы и линейные операции над ними

Определители.

Обратная матрица.Ранг матрицы.

Системы линейных уравнений. Матричный способ решения СЛУ. Формулы Крамера. Метод Гаусса.

Однородные СЛУ.

Декартова система координат. Векторы в пространстве.

Скалярное произведение векторов.

Векторное проиведение векторов.

Смешанное произведение векторов.

10.Прямая на плоскости и ее способы задания.

Плоскость в пространстве

Прямая в пространстве.

Кривые второго порядка.

Поверхность второго порядка

Метод математической индукции.

Множество действительных чисел.Понятие функции.

Понятие предела числовой последовательности.

Непрерывность функции в точке.

Сравнение беск. мал. ф Ф-ии,непрерывные на отрезке

Производная и ее смысл

Уравнение касательной и нормали к кривой.Правила диффиринцирования

Логарифмическое диффиринцирование.

Диффиринциал функции

Производные и дифференциалы высших порядков.

Теоремы Ролля,Лагранжа и Коши.

Правило Лопиталя.

Формула Тейлора

Монотонность и экстремумы функции.

Исследование функции и построение графика.

Вектор-функция .Годограф.

Диффир. длины дуги кривой. Кривизна плоской,пространственной прямой.

Комплексные числа и их изображения.

Формула Муавра и эйлера. Извлечение корня из комплексного числа.

Многочлены и их делимость.Теорема Безу.Основная теорема алгебры. Разложение многочлена на множители.Условие тождественности двух многочленов.Признак кратности корня многочлена и функции .