Алгебраические многочлены. Теорема Безу. Разложение многочлена на множители.

32¹. Алгебраические многочлены. Теорема Безу.

Многочленом или полиномом n-й степени 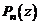будем называть сумму 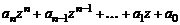, где коэффициенты 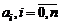, есть комплексные числа и переменная z принимает значения из множества 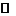. В частности, как 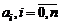, так и z могут быть действительными. Коэффициент 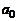называется свободным членом.

Таким образом,

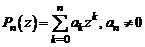. (1)

Число 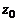называется нулем или корнем многочлена ,
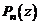если .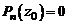

Разделить многочлен 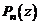на двучлен 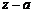, где а есть заданное число, значит представить его в виде

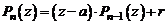, (2)

где 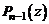есть многочлен степени 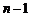, а r называют остатком
от деления многочлена на 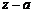. При этом допускают, что равенство (2) выполняетcя для всех значени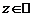й (или 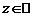). Если 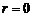, то
говорят, что многочлен делится на .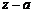

Коэффициенты многочлена 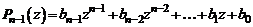и остаток r можно высчитывать согласно рекуррентным формулам

.

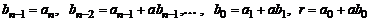При вычислениях используют таблицу

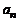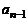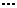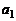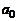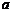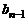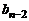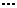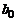Верхняя строка этой таблицы задана, а нижняя постепенно заполняется согласно с заданными выше формулами. Такой способ нахождения некоторого частного и остатка при делении многочлена на двучлен называют схемой Горнера.

Теорема 1 (Безу). Число 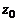является корнем многочлена 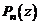тогда и только тогда, когда 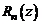делится без остатка на 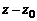, т.е. если

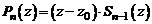, (4)

где 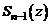– многочлен степени .

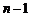Доказательство. Необходимость. Пусть 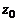– корень многочлена 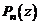, т. е. 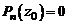. Согласно равенству (2) при 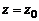имеем 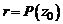. Таким образом, 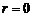, что означает делимость многочле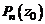на на .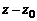

Достаточность. Если многочлен делится на 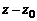, то это означает справедливость равенства (4), откуда следует, что 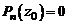. Таким образом, 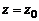есть корень многочлена . □

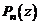Ответ на вопрос о существовании корня многочлена дает следующая теорема.

Теорема 2 (основная теорема алгебры). Всякий многочлен положительной степени имеет хотя бы один корень (действительный или комплексный).

32². Разложение многочлена на множители.

1⁰.Число 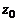называется корнем многочлена 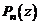кратности k, если 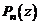можно представить в виде

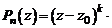
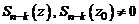. (1)

Другими словами, если 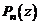делится без остатка на 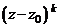и не делится на 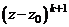, то k называется кратностью корня .

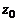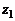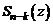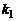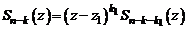Если, в свою очередь, число является корнем многочлена кратности , то , где 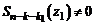. Продолжая этот процесс, через конечное число шагов m получим многочлен нулевой степени 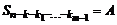, причем .

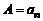Таким образом, если 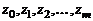– корни многочлена 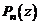кратности 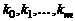, соответственно, причем 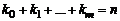, то имеет место следующее разложение многочлена 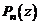на множители

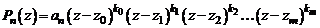, (2)

т.е. всякий многочлен n-й степени раскладывается на n линейных множителей типа 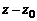и числовой множитель, равный коэффициенту при .

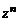Пусть 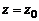есть действительный корень кратности k многочлена 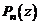с действительными коэффициентами. Тогда этот многочлен можно записать в виде (1).

Пусть теперь 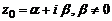, есть комплексный корень многочлена 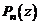, тогда и число 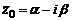также будет корнем этого многочлена. Действительно, используя свойства комплексно-сопряженных чисел, получим

.

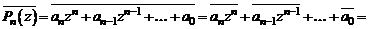
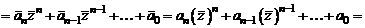
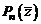Отсюда, если 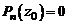, то 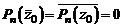, т. е. 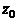– корень многочлена .

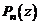Следовательно, в разложении многочлена 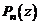на множители будет присутствовать произведение .

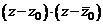Отсюда следует, если 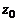– корень кратности k, то и 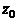− корень кратности k. Другими словами, многочлен 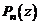в этом случае можно представить в виде

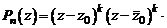
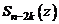. (3)

Имеем

,

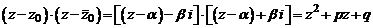где 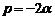, 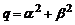– действительные числа.

Легко видеть, что трехчлен 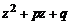имеет дискриминант .

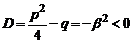Таким образом, если 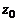– комплексный корень трехчлена 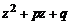, то дискриминант 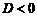. Справедливо и обратное: если 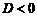, то трехчлен имеет комплексно-сопряженные корни:

.

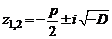Из вышеизложенного вытекает: есл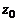и и 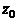− комплексно-сопряженные корни многочлена 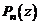кратности k, то, в силу представления (3), имеет место разложение

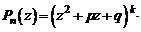
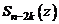, (3^/)

где 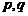– действительные числа, 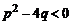, а для многочлена 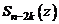с действительными коэффициентами числа 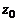, 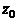не являются его корнями, т.е. , .

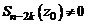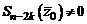Пусть 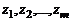– все действительные корни многочлена 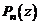, а их кратности соответственно равны 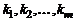, где 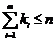. Тогда многочлен 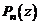, согласно формуле (1), можно представить в ви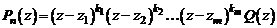де , где 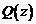– многочлен степени 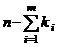с действительными коэффициентами,

который не имеет действительных корней.

Если 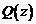– многочлен ненулевой степени, то каждой паре комплексно-сопряженных корней 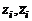кратности 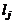соответствует множитель 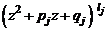из формулы (3^/), где .
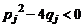С учетом этого обстоятельства получим

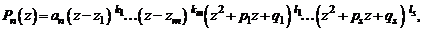(4)

где .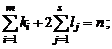

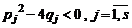Таким образом, зная все корни многочлена 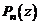с действительными коэффициентами, можно его разложить на множители с действительными коэффициентами, это значит представить в виде (4), где числа 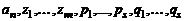– действительные.

2⁰. Тождественность двух многочленов. Выясним условие, при котором два многочлена тождественны. Перейдем здесь от обозначения переменной z к x, подчеркивая тем самым, что все дальнейшие рассмотрения будут проводиться в области действительных чисел.

Утверждение 1.Многочлен 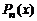равен нулю тогда и только тогда, когда все его коэффициенты равны нулю.

Доказательство.Действительно, согласно формуле (2), многочлен 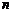-ой степени 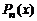можно представить в виде

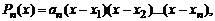(2΄)

где 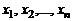– корни этого многочлена, среди которых могут быть и равные.

Из разложения (2΄) следует, что многочлен 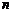-ой степени не может иметь более чем 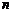корней с учетом их кратности. Если же он обращается в нуль при 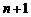различных значениях 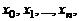то этот многочлен тождественно равен нулю. В самом деле, т.к. 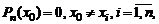но ни один из его линейных множителей в (2΄) не равен нулю, следует, что 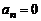, а значит, согласно той же формуле (2), 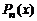тождественно равен нулю.

Обратно, если многочлен тождественно равен нулю, то он равен нулю и при некотором значении 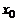переменной 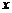, которое не совпадает с 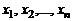. В таком случае ни один из множителей 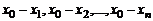не равен нулю, а поэтому 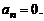Повторяя рассуждения для многочлена 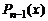уже с высшим коэффициентом 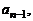аналогично показываем, что 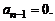Таким же образом доказывается ☐

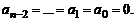Утверждение 2. Два многочлена 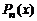и 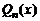тождественно равны друг другу тогда и только тогда, когда у них совпадают коэффициенты при одинаковых степенях .

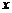Доказательство. Это утверждение следует из того, что разность данных многочленов есть многочлен, тождественно равный нулю. Тогда, на основании утверждения 1, все его коэффициенты равны нулю. ☐

3⁰. Признак кратности корня.

Утверждение 3. Если 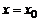– корень кратности k многочлена 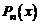, то 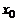является корнем кратности 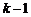его производной .

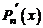Доказательство.Действительно, если 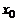− корень кратности k многочлена 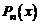, то имеет место представление

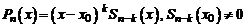. (5)

Дифференцируя это равенство, получаем

,

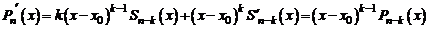где 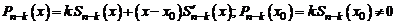, т.е. 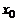является корнем кратности 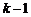производной . □

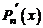Следствие 1. Для того, чтобы число 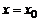было корнем кратности 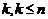, многочлена 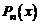необходимо и достаточно, чтобы

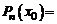
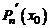
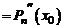
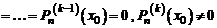. (6)

Множество действительных чисел. Модуль действительного числа. Ограниченные и неограниченные числовые множества. Наибольший и наименьший элементы числового множества. Верхняя и нижняя грани числового множества.

33¹. Множество действительных чисел.

Целые положительные числа 1,2,3… называются натуральными. Множество натуральных чисел обозначают N.

Рациональные числа – все целые, нуль и дробные числа.

Каждое рациональное число можно представить в виде 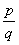, где p – целое число, q – натуральное число.

Рациональное число можно представить также в виде периодической десятичной дроби. Иррациональные числа – бесконечная непериодическая дробь.

Все рациональные и иррациональные числа образуют множество действительных чисел, которое обозначают R.

Каждое действительное число изображается точкой числовой оси и, обратно, каждой точке числовой оси соответствует единственное действительное число.

1. Интервалом называется множество действительных чисел х, удовлетворяющих неравенству a < x < b, где a, b – действительные числа. Обозначается (a,b).

2. Отрезком (сегментом) называется множество действительных чисел, удовлетворяющих неравенству a ≤ x ≤ b. Обозначается [a, b].

3. Интервал длины 2ε, с центром в точке х₀ называют окрестностью точки х₀х₀ – ε < х < х₀ + ε .

4. Интервалы могут быть бесконечные: (а, + ∞), (- ∞, а), (-∞, +∞), [a, + ∞),

(- ∞, a].

33². Модуль действительного числа. Ограниченные и неограниченные числовые множества.