Каноническое разложение многочлена на множители
1) Если 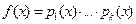 – разложение многочлена
– разложение многочлена 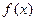 на неприводимые множители и
на неприводимые множители и 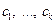 – старшие коэффициенты многочленов
– старшие коэффициенты многочленов 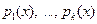 соответственно, то это разложение
соответственно, то это разложение 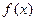 можно записать в виде:
можно записать в виде: 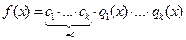 , где
, где 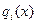 – неприводимый многочлен со старшим коэффициентом, равным 1
– неприводимый многочлен со старшим коэффициентом, равным 1 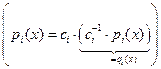 .
.
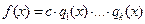 . В этой форме разложение единственно с точностью до порядка следования сомножителей.
. В этой форме разложение единственно с точностью до порядка следования сомножителей.
2) В разложении 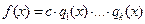 среди сомножителей могут быть равные и их можно объединить в степени. Тогда разложение примет вид:
среди сомножителей могут быть равные и их можно объединить в степени. Тогда разложение примет вид: 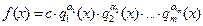 , где
, где 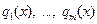 – попарно различные неприводимые над Р многочлены со старшими коэффициентами, равными 1 (нормированные многочлены),
– попарно различные неприводимые над Р многочлены со старшими коэффициентами, равными 1 (нормированные многочлены), 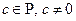 . Такое разложение многочлена
. Такое разложение многочлена 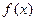 называют каноническим разложением многочлена f(x) на множители.
называют каноническим разложением многочлена f(x) на множители.
ВОПРОС № 9 Разложение многочлена на неприводимые множители над полем комплексных и над полем действительных чисел.
п. 1. Многочлены над полем комплексных чисел 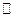 .
.
Опр.1. Многочлен 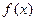 кольца
кольца 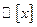 степени
степени 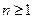 называется приводимым над полем
называется приводимым над полем 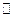 , если
, если 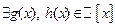 , такие что
, такие что 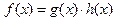 , причем
, причем 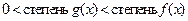 и
и 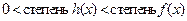 . В противном случае, многочлен
. В противном случае, многочлен 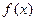 называется неприводимым над
называется неприводимым над 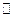 .
.
Справедлива так называемая основная теорема алгебры:
Теорема 1. Всякий многочлен с комплексными коэффициентами степени 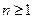 имеет хотя бы один комплексный корень.
имеет хотя бы один комплексный корень.
Внимание: необходимо знать понятие корня многочлена: если 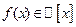 , то
, то 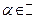 называется корнем
называется корнем 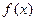 , если
, если 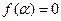 .
.
Теорема 2. Над полем комплексных чисел неприводимыми являются только многочлены первой степени.
Доказательство вытекает из теоремы 1.
Как известно, всякий многочлен 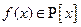 степени
степени 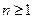 может быть представлен в виде:
может быть представлен в виде: 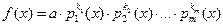 , где
, где 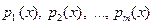 – попарно различные нормированные неприводимые над Р многочлены (это так называемое каноническое разложение многочлена
– попарно различные нормированные неприводимые над Р многочлены (это так называемое каноническое разложение многочлена 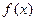 ).
).
Поэтому имеет место следующее предложение: Каноническое разложение многочлена 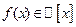 степени
степени 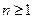 имеет вид:
имеет вид: 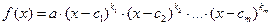 , где
, где 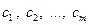 – попарно различные комплексные числа.
– попарно различные комплексные числа.
Следствие: Многочлен 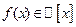 степени
степени 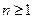 имеет ровно п корней, считая каждый корень столько раз, какова его кратность.
имеет ровно п корней, считая каждый корень столько раз, какова его кратность.
п. 2. Многочлены над полем действительных чисел 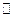 .
.
Пусть 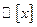 – кольцо многочленов над полем действительных чисел
– кольцо многочленов над полем действительных чисел 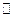 .
.
Напомним, что комплексное число 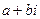 , где
, где 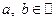 называется мнимым, если
называется мнимым, если 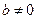 . Если
. Если 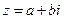 , то через
, то через 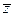 будем обозначать сопряженное комплексное число
будем обозначать сопряженное комплексное число 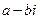 .
.
Используя свойства сопряженных комплексных чисел 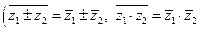 ,
,
если 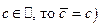 , легко доказать следующее предложение:
, легко доказать следующее предложение:
Предложение 1: Если 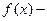 многочлен из кольца
многочлен из кольца 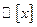 и z – произвольное комплексное число, то
и z – произвольное комплексное число, то 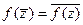 .
.
Доказательство: Пусть 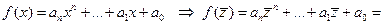
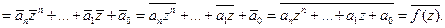 ▲.
▲.
Теорема 3. Пусть 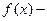 произвольный многочлен из кольца
произвольный многочлен из кольца 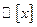 . Если
. Если 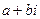 – мнимый корень многочлена
– мнимый корень многочлена 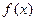 , то число
, то число 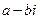 также является корнем этого многочлена.
также является корнем этого многочлена.
Доказательство: Так как 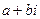 – корень
– корень 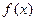 , то
, то 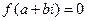 . Тогда по предложению 1,
. Тогда по предложению 1, 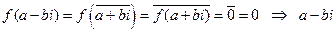 – корень
– корень 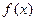 . ▲.
. ▲.
