Миноры и алгебраические дополнение элемента определителя.

Минором элемента a_ijопределителя порядка n называется определитель n-1-го порядка, полученный из исходного вычеркивания i-ой строки j-го столбца.

Алгебраическим дополнением элемента a_ijс определителем ∆наз. Соответствующие минором взятом i+j-числа, «+» если i+j-четна, «-» если i+j-нечетна.

Свойства определителей.

Свойства:

1)Определитель не изменится, если его строки заменить соответствующими столбцами и наоборот.

2)Если поменять местами два параллельных ряда определителя, то определитель изменит знак.

3)Определитель с двумя одинаковыми параллельными рядами равен 0.

4)Общий множитель, какого – либо ряда можно вынести за знак определителя.

5)Определитель, у которого элементы двух рядов соответственно пропорционален, то он =0.

6)Если все элементы какого-либо ряда определителя равны 0, то и сам определитель равен 0.

7)Определитель не изменится, если к элементам одного ряда прибавить соответственно элементы другого параллельного ряда, умножить на одно и то же число.

8)Определитель равен сумме произведения элементов любого ряда на их алгебраическое дополнение.

Невырожденная матрица. Союзная матрица. Обратная матрица. Теорема о существовании обратной матрицы.

Квадратная матрица А наз. не выраженной, если detA¹0. В противном случае (detA=0) –выражденной.

Союзной матрицей А наз. матрица А*

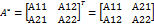
Матрица А^-1 наз. обратной к матрице А, если выполняются следующие действия:

А×А^{-1 =} А^-1×А = Е, где Е – единичная матрица, того же размера, что и А.

Теорема. Для данной матрицы А, существует единственная обратнаяматрица А^-1ÛdetA≠0.

Формула для нахождения обратной матрицы:

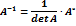
Свойства обратной матрицы.

Свойства:

1) det (A^-1) =1/detA

2) (AB)^-1=A^-1×B^-1

3) (A^-1)^T=(A^T)^-1

Рангматрицы.Свойства ранга матрицы.

Рангом матрицы наз. наибольший из порядков, отличный от 0 миноров этой матрицы. (rA или rangA)

Свойства ранга матрицы:

1)ранг матрицы не меняется при трансформировании

2)ранг матрицы не изменится, если из неё вычеркнуть нулевой ряд

3)если у матрицы есть несколько одинаковых, пропорциональных, параллельных рядов, то можно 1 из них оставить, остальные вычеркнуть, ранг не изменится.

4)ранг матрицы не меняется при элементарных преобразованиях

Системы линейных уравнений: однородные, неоднородные, совместные, несовместные, определённые, неопределённые.

Дана системаm линейных алгебраических уравнений с n неизвестных

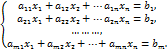
Где числа a_n-коэффициенты системы, а числа b_i-свободные члены.

Если все b_i=0 (свободные члены), то система называется однородной, в противном случае – неоднородной.

Система называется совместной, если она имеет хотя бы одно решение, и несовместной – если она не имеет ни одного решения.

Совместная система называется определенной, если она имеет единственное решение. Система, имеющая более одного решения наз. неопределённой.