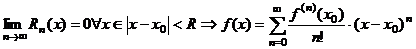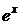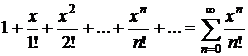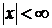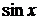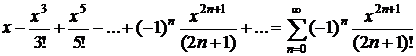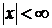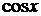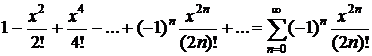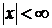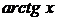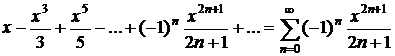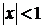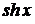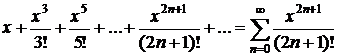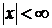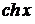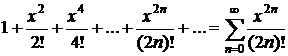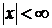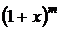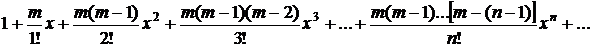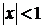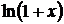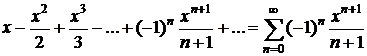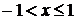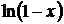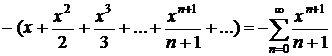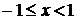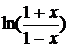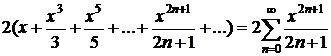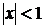| Определение | 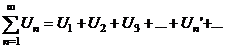 , , 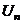 - действительные числа произвольного признака В частности, - действительные числа произвольного признака В частности, 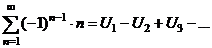 , , 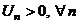 - знакочередующийся ряд - знакочередующийся ряд |
| Абсолютная и условная сходимость знакопеременных рядов | 1. 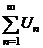 и и 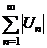 сходятся сходятся  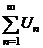 - абсолютно сходится 2. - абсолютно сходится 2. 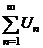 сходится, а сходится, а 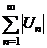 расходится расходится  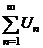 - условно сходится - условно сходится |
| Достаточные признаки сходимости знакопеременных рядов |
| Признак абсолютной сходимости | Признак Лейбница |
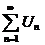 - знакопеременный - знакопеременный 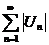 сходится сходится  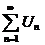 абсолютно сходится абсолютно сходится | 1) 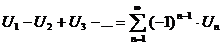 | | 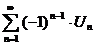 сходится сходится |
2) 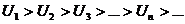 | Þ | 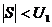 |
3) 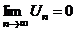 | | 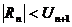 |
Замечание: 1. В сходящемся знакочередующемся ряде 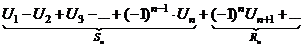 сумма S может быть заменена сумма S может быть заменена 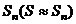 . Получаемая погрешность . Получаемая погрешность 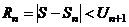 2. Убывание модулей членов знакопеременного ряда можно доказать с помощью производной. Если 2. Убывание модулей членов знакопеременного ряда можно доказать с помощью производной. Если 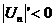 с некоторого номера, то члены ряда с некоторого номера, то члены ряда 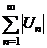 убывают с этого номера. 3. Если расходимость ряда убывают с этого номера. 3. Если расходимость ряда 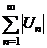 установлена признаком Даламбера или признаком Коши, то и ряд установлена признаком Даламбера или признаком Коши, то и ряд 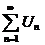 расходится, т. к. если расходится, т. к. если 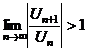 или или 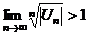 , то , то 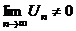 . . |
Алгоритм исследования знакопеременного ряда 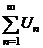 на сходимость. на сходимость. |
1. Составить ряд из абсолютных членов данного ряда 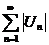 и исследовать его сходимость. 2. а) и исследовать его сходимость. 2. а) 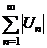 сходится сходится  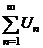 абсолютно сходится; б) абсолютно сходится; б) 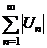 расходится расходится  исследуй 3. 3. Проверить условия признака Лейбница Если 1) члены чередуются по знаку; 2) исследуй 3. 3. Проверить условия признака Лейбница Если 1) члены чередуются по знаку; 2) 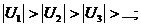 3) 3) 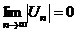 то 1) то 1) 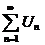 сходится по признаку Лейбница 2) сходится по признаку Лейбница 2) 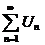 условно сходится, т. к. условно сходится, т. к. 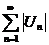 расходится расходится |
| | | | | |
Функциональные ряды. Основные понятия
| Понятие | Определение и обозначение |
| 1. Функциональный ряд | 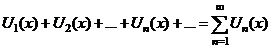 |
| 2. Члены ряда | 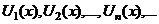 - функции от - функции от 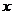 |
3. Сходимость ряда в точке 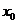 | 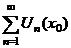 сходится сходится  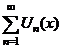 сходится в т. сходится в т. 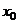 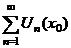 расходится расходится  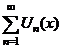 расходится в т. расходится в т. 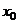 |
| 4. Область сходимости ряда | 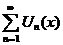 сходится сходится 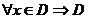 - область сходимости; - область сходимости;  - находится: - находится: 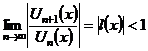 или или 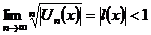 , , |
| 5. Последовательность частичных сумм | 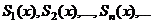 , где , где 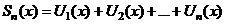 , , 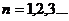 |
| 6. Сумма сходящегося ряда | 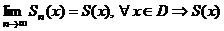 - сумма ряда - сумма ряда |
| 7. Остаток ряда | 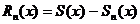 |
8. Равномерная сходимость ряда 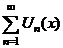 на на  | 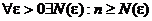 и и 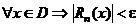 |
| 9. Абсолютная и равномерная сходимость ряда (признак Вейерштрасса) | 1. 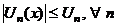 и и 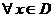 2. числовой ряд 2. числовой ряд 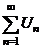 - сходится - сходится | Þ | 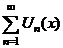 - сходится абсолютно и равномерно на - сходится абсолютно и равномерно на  |
| Свойства равномерно сходящихся рядов |
1. 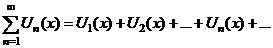 - равномерно сходится на - равномерно сходится на  2. 2. 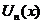 - непрерывна - непрерывна 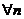 и и 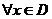 3. 3. 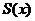 - его сумма - его сумма 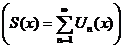 | Þ | 1. 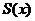 - непрерывна на - непрерывна на  2. 2. 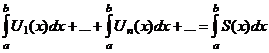 , где , где 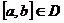 (почленное интегрирование) 3. (почленное интегрирование) 3. 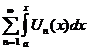 - равномерно сходится на - равномерно сходится на  , где , где 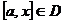 |
1. 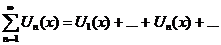 - сходится на - сходится на  , , 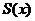 - его сумма 2. - его сумма 2. 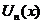 - дифференцируемые - дифференцируемые 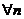 и и 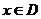 3. 3. 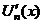 - непрерывны - непрерывны 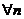 и и 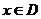 4. 4. 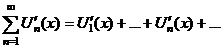 - равномерно сходится на - равномерно сходится на  | Þ | 1. 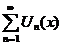 - равномерно сходится на - равномерно сходится на  2. 2. 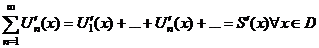 (почленное дифференцирование) (почленное дифференцирование) |
| | | | | | |
Степенные ряды
| Определение и обозначение | (1) 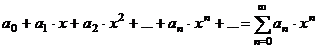 |
(2) 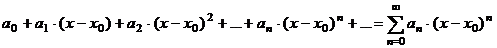 , где , где 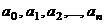 - постоянные коэффициенты - постоянные коэффициенты |
| Радиус сходимости. Основная теорема | Для рядов (1) и (2) 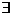 число число 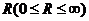 , обладающие свойствами, , обладающие свойствами, 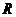 - радиус сходимости - радиус сходимости |
1) 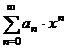 при при 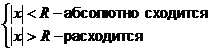 |  |
2) 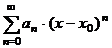 при при 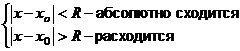 | 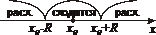 |
| Свойства степенных рядов | 1. 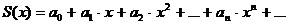 , , 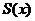 - непрерывна - непрерывна 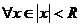 2. 2. 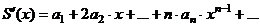 - сходится - сходится 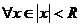 3. 3. 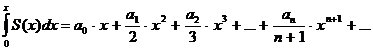 - сходится - сходится 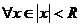 |
| Алгоритм определения интервала сходимости | 1.Найти 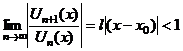 или или 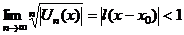 2.Решить неравенство 2.Решить неравенство 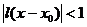 , получить интервал сходимости , получить интервал сходимости 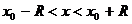 3.Исследовать сходимость ряда на концах полученного интервала 3.Исследовать сходимость ряда на концах полученного интервала |
Разложение функции в степенной ряд
Ряд Тейлора (по степеням 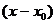 ) ) | 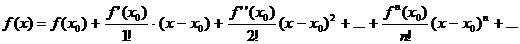 |
Ряд Маклорена (по степеням 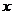 ) ) | 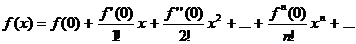 |
| Алгоритм разложения функции в степенной ряд. | 1. Найти все производные 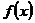 в точке в точке 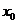 : : 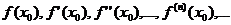 2. записать ряд Тейлора для 2. записать ряд Тейлора для 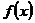 : : 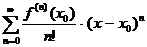 3. Найти интервал сходимости 3. Найти интервал сходимости 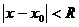 полученного ряда 4. Найти полученного ряда 4. Найти 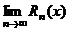 , где , где 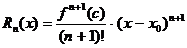 - остаточный член формулы Тейлора - остаточный член формулы Тейлора 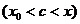 5. Если 5. Если 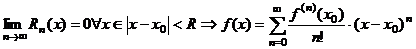 |
Таблица разложений некоторых функций в степенные ряды
| № п/п | Функция | Разложение в ряд | Интервал сходимости |
| | 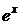 | 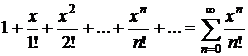 | 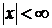 |
| | 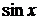 | 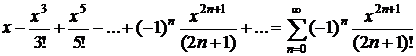 | 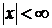 |
| | 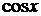 | 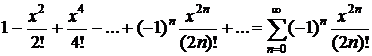 | 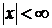 |
| | 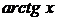 | 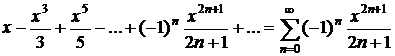 | 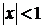 |
| | 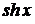 | 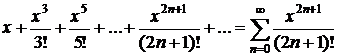 | 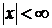 |
| | 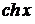 | 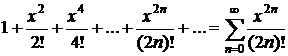 | 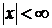 |
| | 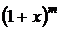 | 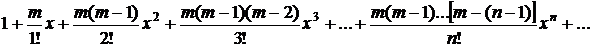 | 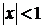 |
| | 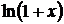 | 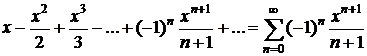 | 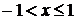 |
| | 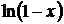 | 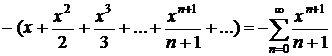 | 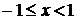 |
| | 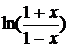 | 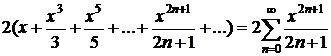 | 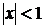 |
Наши рекомендации
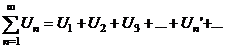 ,
, 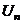 - действительные числа произвольного признака В частности,
- действительные числа произвольного признака В частности, 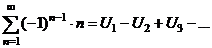 ,
, 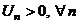 - знакочередующийся ряд
- знакочередующийся ряд 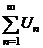 и
и 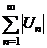 сходятся
сходятся 
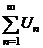 - абсолютно сходится 2.
- абсолютно сходится 2. 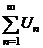 сходится, а
сходится, а 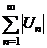 расходится
расходится 
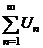 - условно сходится
- условно сходится 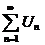 - знакопеременный
- знакопеременный 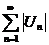 сходится
сходится 
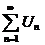 абсолютно сходится
абсолютно сходится 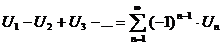
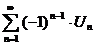 сходится
сходится 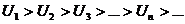
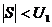
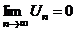
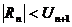
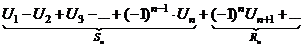 сумма S может быть заменена
сумма S может быть заменена 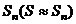 . Получаемая погрешность
. Получаемая погрешность 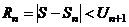 2. Убывание модулей членов знакопеременного ряда можно доказать с помощью производной. Если
2. Убывание модулей членов знакопеременного ряда можно доказать с помощью производной. Если 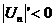 с некоторого номера, то члены ряда
с некоторого номера, то члены ряда 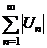 убывают с этого номера. 3. Если расходимость ряда
убывают с этого номера. 3. Если расходимость ряда 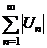 установлена признаком Даламбера или признаком Коши, то и ряд
установлена признаком Даламбера или признаком Коши, то и ряд 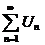 расходится, т. к. если
расходится, т. к. если 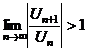 или
или 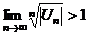 , то
, то 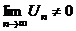 .
. 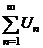 на сходимость.
на сходимость. 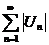 и исследовать его сходимость. 2. а)
и исследовать его сходимость. 2. а) 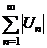 сходится
сходится 
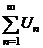 абсолютно сходится; б)
абсолютно сходится; б) 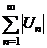 расходится
расходится  исследуй 3. 3. Проверить условия признака Лейбница Если 1) члены чередуются по знаку; 2)
исследуй 3. 3. Проверить условия признака Лейбница Если 1) члены чередуются по знаку; 2) 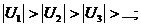 3)
3) 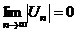 то 1)
то 1) 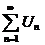 сходится по признаку Лейбница 2)
сходится по признаку Лейбница 2) 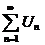 условно сходится, т. к.
условно сходится, т. к. 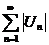 расходится
расходится 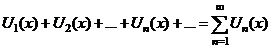
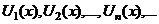 - функции от
- функции от 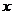
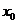
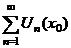 сходится
сходится 
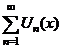 сходится в т.
сходится в т. 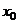
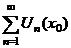 расходится
расходится 
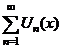 расходится в т.
расходится в т. 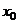
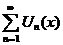 сходится
сходится 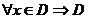 - область сходимости;
- область сходимости;  - находится:
- находится: 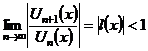 или
или 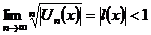 ,
, 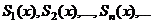 , где
, где 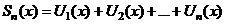 ,
, 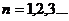
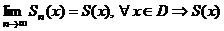 - сумма ряда
- сумма ряда 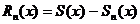
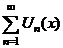 на
на 
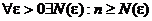 и
и 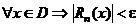
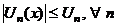 и
и 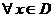 2. числовой ряд
2. числовой ряд 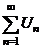 - сходится
- сходится 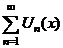 - сходится абсолютно и равномерно на
- сходится абсолютно и равномерно на 
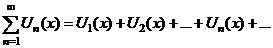 - равномерно сходится на
- равномерно сходится на  2.
2. 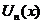 - непрерывна
- непрерывна 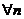 и
и 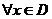 3.
3. 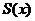 - его сумма
- его сумма 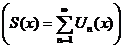
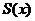 - непрерывна на
- непрерывна на  2.
2. 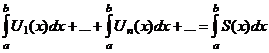 , где
, где 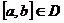 (почленное интегрирование) 3.
(почленное интегрирование) 3. 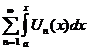 - равномерно сходится на
- равномерно сходится на  , где
, где 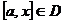
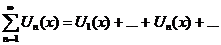 - сходится на
- сходится на  ,
, 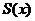 - его сумма 2.
- его сумма 2. 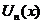 - дифференцируемые
- дифференцируемые 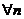 и
и 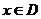 3.
3. 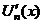 - непрерывны
- непрерывны 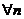 и
и 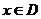 4.
4. 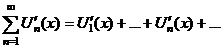 - равномерно сходится на
- равномерно сходится на 
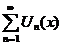 - равномерно сходится на
- равномерно сходится на  2.
2. 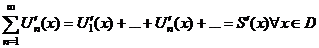 (почленное дифференцирование)
(почленное дифференцирование) 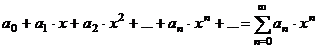
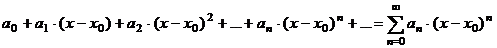 , где
, где 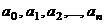 - постоянные коэффициенты
- постоянные коэффициенты 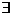 число
число 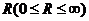 , обладающие свойствами,
, обладающие свойствами, 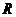 - радиус сходимости
- радиус сходимости 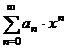 при
при 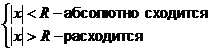

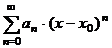 при
при 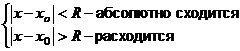
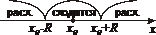
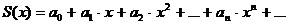 ,
, 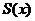 - непрерывна
- непрерывна 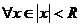 2.
2. 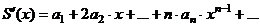 - сходится
- сходится 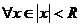 3.
3. 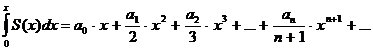 - сходится
- сходится 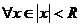
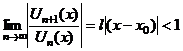 или
или 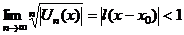 2.Решить неравенство
2.Решить неравенство 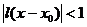 , получить интервал сходимости
, получить интервал сходимости 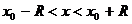 3.Исследовать сходимость ряда на концах полученного интервала
3.Исследовать сходимость ряда на концах полученного интервала 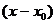 )
) 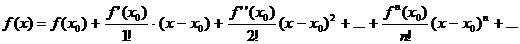
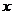 )
) 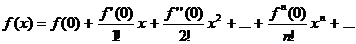
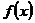 в точке
в точке 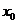 :
: 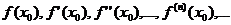 2. записать ряд Тейлора для
2. записать ряд Тейлора для 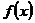 :
: 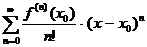 3. Найти интервал сходимости
3. Найти интервал сходимости 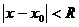 полученного ряда 4. Найти
полученного ряда 4. Найти 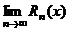 , где
, где 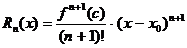 - остаточный член формулы Тейлора
- остаточный член формулы Тейлора 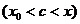 5. Если
5. Если