Тема: Внетабличное умножение и деление

План:

1. Общая характеристика темы.

2. Теоретическая основа изучения внетабличного умножения:

а) правило умножения суммы на число;

б) умножение десятков на число;

в) формирование вычислительного приема;

3. Теоретическая основа изучения внетабличного деления:

а) правило деления суммы на число;

б) деление десятков на число;

в) формирование вычислительного навыка.

4. Деление двузначного числа на двузначное.

5. Последовательность изучения деления с остатком.

6. Частные и особые случаи умножения и деления с 0 и 1.

7. Анализ методических статей по теме.

Рекомендательная литература

1. Уткина Н.Г. Изучение трудных тем по математике. – С. 71-88.

2. Вапняр Н.Ф. Изучение темы «Деление с остатком» // Начальная школа. – 1981. - №1. – С. 36-38.

3. Степанова С.В. Случаи умножения и деления с числами 0 и 1 // Начальная школа. – 1984. - №10. – С. 42-45.

4. Ивашова О.А. К вопросу о рационализации вычислений // Начальная школа. – 1998. – №2. – С. 86-90.

Внетабличное умножение и деление изучается в следующей последовательности:

1. Умножение и деление разрядных чисел вида 20·3; 3·20; 60:2; 80:20;

2. Правило умножения суммы на число;

3. Умножение двузначного числа на однозначное;

4. Правило деления суммы на число;

5. Деление двузначного числа на однозначное;

6. Деление двузначного числа на двузначное;

7. Умножение и деление разрядных чисел.

Умножение и деление разрядных чисел сводится к умножению и делению однозначных чисел:

20 · 4 =		60 : 2 =		2 · 30 =
2 д. · 4 = 8 д.		6 д. : 2 = 3 д.		30 · 2 = 60

Правило умножения суммы на число

Правило умножения суммы на число выполняет роль теоретического обоснования умножения двузначного числа на однозначное, а правило деления суммы на число - деления двузначного числа на однозначное. Методику изучения правил рассмотрим на примере правила умножения суммы на число.

При изучении этого правила ребенок должен понять, что суммы на число можно умножить двумя способами: 1) вычислить сумму и результат умножить на число; 2) каждое слагаемое умножить на число и полученные результаты сложить. Для этого целесообразно использовать следующую наглядность:

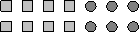
На этом рисунке изображены два ряда геометрических фигур, по 4 квадрата и 3 кружка в каждом ряду. Нужно посчитать, сколько всего геометрических фигур изображено на рисунке. Это можно сделать двумя способами:

1) сложить количество кружков и квадратов в одном ряду ( 4 + 3) и полученный результат умножить на 2:

(4 + 3) · 2 = 7 · 2 = 14;

2) отдельно посчитать квадраты и отдельно – кружки, а затем полученные результаты сложить:

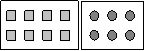
(4 + 3) · 2 = 4 · 2 + 3 · 2 = 8 + 6 = 14.

Умножение двузначного числа на однозначное

Освоение приема умножения двузначного числа на однозначное осуществляется в следующей последовательности:

1) Выполнение приема на уровне предметных действий. Например, при решении примера 23 · 4 можно четыре раза взять по два пучка палочек (число 20) и по три отдельных палочки.

2) Моделирование предметных действий в виде схемы:

23 · 4 = 92.

1)Числовая запись вычислительного приема:

23 · 4 = (20 + 3) · 4 = 20 · 4 + 3 · 4 = 80 + 12 = 92.

При выполнении данного вычислительного приема требуются следующие опорные знания: а) замена двузначного числа суммой разрядных слагаемых (23 = 20 + 3); б) умножение разрядного числа на однозначное (20 · 4); в) табличное умножение (3 · 4); г) сложение двузначных чисел (80 + 12). Все эти опорные знания необходимо включить в подготовительный этап, предшествующий освоению вычислительного приема.

Аналогичным образом изучается деление двузначного числа на однозначное.

Деление двузначного числа на двузначное

Деление двузначного числа на двузначное производится методом подбора, например, решая пример 72 : 12, ребенок рассуждает следующим образом: «Подберем число, которое при умножении на 12 даст число 72. это будет число 6. значит, 72 12 = 6».

Деление с остатком

Основное назначение данной темы – подготовить ребенка к выполнению деления многозначных чисел «уголком».

На первом этапе следует обратить его внимание на то, что не всегда одно число делится на другое. В этом случае говорят о делении с остатком. Запись деления с остатком выглядит так:

17 : 3 = 5 (ост. 2).

На следующем этапе осуществляется знакомство с основным свойством деления с остатком: остаток от деления всегда меньше делителя. Это можно сделать следующим образом. Выберем несколько чисел, например: 12, 13, 14, 15, 16, 17. Будем поочередно каждое из этих чисел делить на числа 2. 3, 4, фиксируя получившиеся при этом остатки. Это удобно сделать в виде таблицы:

Делитель	Остаток
	0, 1
	0, 1, 2
	0, 1, 2, 3

Сравнивая остатки с делителем, ребенок может сам сделать вывод о том, что остаток всегда меньше делителя. В противном случае цифру частного можно увеличить на единицу.

Особые случаи умножения и деления

Умножение единицы на число:

1 · 4 = 4.

Основание: 1 · 4 = 1 + 1 + 1 + 1 = 4.

Умножение числа на единицу:

3 · 1 = 3.

Обоснование: этот случай нельзя обосновать путем перехода к сложению («взять число 3 слагаемым один раз»), т.к. сумм с одним слагаемым не существует. Поэтому данный случай является исключением и не обосновывается, а вводится в виде правила: «При умножении любого числа на 1 получается то же самое число».

Деление на единицу:

5 : 1 = 5.

Обоснование проводится путем перехода от деления к умножению: «Какое число нужно умножить на 1, чтобы получить 5? Число 5. Значит, 5 разделить на 1 будет 5».

Умножение и деление с числом 10:

10 · 4 = 40; 4 · 10 = 40; 40 : 4 = 10; 40 : 10 = 4.

Обоснование. Так как 10 = 1 дес., то данные случаи сводятся к умножению и делению с числом 1.

Умножение нуля на число:

0 4 = 0.

Обоснование: 0 · 4 = 0 + 0 + 0 + 0 = 0.

Умножение числа на нуль:

3 · 0 = 0.

Обоснование: этот случай также нельзя обосновать путем перехода к сложению («взять число 3 слагаемым нуль раз»), т.к. сумм с нулем слагаемых не существует. поэтому данный случай также является исключением и не обосновывается, а вводится в виде правила: «При умножении любого числа на нуль получается нуль».

Деление числа на нуль:

5 : 0 = ?

Обоснование проводится также путем перехода от деления к умножению: «Какое число нужно умножить на 0, чтобы получить 5? Такого числа не существует. Значит, на нуль делить нельзя!»