Наивероятнейшее число появления событ. в последовательности независим. испытаний
Опред.: Наивероятнейш. числом 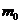 наступления соб. А в n независим. испытаниях назыв. число, для кот. вероятн.
наступления соб. А в n независим. испытаниях назыв. число, для кот. вероятн. 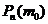 превышает или по крайней мере не менее вер. каждого из остальных возможн. исходов испытаний. Пусть соб. А наступило
превышает или по крайней мере не менее вер. каждого из остальных возможн. исходов испытаний. Пусть соб. А наступило 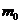 раз в n испытаниях. Вер. появл. соб. А обозначим p; P(A)=p, а
раз в n испытаниях. Вер. появл. соб. А обозначим p; P(A)=p, а 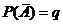 , тогда по формуле Бернули
, тогда по формуле Бернули 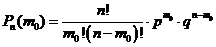 . По определению:
. По определению: 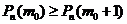 -формула (1);
-формула (1); 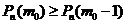 -формула (2). Из нер-ва (1) получаем:
-формула (2). Из нер-ва (1) получаем: 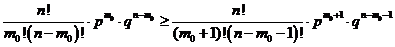 ;
; 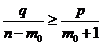 ;
; 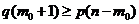 ;
; 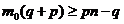 . Т.к.
. Т.к. 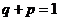 , то
, то 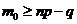 . Из нер-ва (2) получаем:
. Из нер-ва (2) получаем: 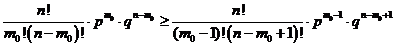 ;
; 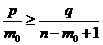 ;
; 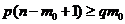 ;
; 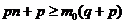 ;
; 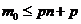 . Т,о. для нахождения наивероятнейш. числа мы получили нер-во:
. Т,о. для нахождения наивероятнейш. числа мы получили нер-во: 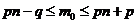 . Замечание 1: Длина интервала, определяемая последн. нер-вом равна 1; Замечание 2: Если границы интервала – дробные числа, то значение наивероятнейш. числа одно. Если границы – целые числа, то значений наивер. числа два.
. Замечание 1: Длина интервала, определяемая последн. нер-вом равна 1; Замечание 2: Если границы интервала – дробные числа, то значение наивероятнейш. числа одно. Если границы – целые числа, то значений наивер. числа два.
Функция Лапласа. Интегральная функц. Лапласа. Их применение для решения задач в условиях повторения испытаний.
Использовать формулу Бернулли при достаточно большом кол-ве испытаний затруднительно. Поэтому, когда 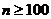 используют теорему Лапласа. Локальная теорема Лапласа: Если вер. появления соб. А в кажд. испытании постоянна и отлична от 0 и 1, то вер.
используют теорему Лапласа. Локальная теорема Лапласа: Если вер. появления соб. А в кажд. испытании постоянна и отлична от 0 и 1, то вер. 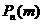 того, что соб. А появится в n испытаниях ровно m раз, приближен. равна(тем точнее, чем больше n) значению функции:
того, что соб. А появится в n испытаниях ровно m раз, приближен. равна(тем точнее, чем больше n) значению функции: 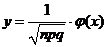 , где
, где 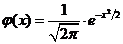 , где
, где 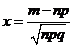 . Имеются таблицы, в кот. помещены значения функц.
. Имеются таблицы, в кот. помещены значения функц. 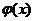 , соответствующ. положит. значениям аргумента
, соответствующ. положит. значениям аргумента 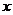 . Для отрицат. значений аргумента пользуются теми же таблицами, т.к. функц.
. Для отрицат. значений аргумента пользуются теми же таблицами, т.к. функц. 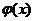 четная, т.е.
четная, т.е. 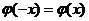 . Вер. того, что соб. А появится в n испытаниях ровно m раз
. Вер. того, что соб. А появится в n испытаниях ровно m раз 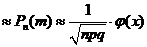 , где
, где 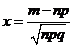 . Предположим, что производится n испытаний, в кажд. из кот. вер. появл. соб. А постоянна и равна p,
. Предположим, что производится n испытаний, в кажд. из кот. вер. появл. соб. А постоянна и равна p, 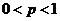 . Нужно найти вер того, что соб. А появится в n испытаниях не менее
. Нужно найти вер того, что соб. А появится в n испытаниях не менее 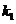 и не более
и не более 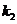 раз, т.е. нужно найти
раз, т.е. нужно найти 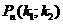 . Теор.: Если вер. P наступления события в кажд. испытании постоянна и отлична от 0 и 1, то вер.
. Теор.: Если вер. P наступления события в кажд. испытании постоянна и отлична от 0 и 1, то вер. 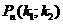 того, что в n испытаниях соб. А появится от
того, что в n испытаниях соб. А появится от 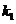 до
до 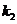 раз
раз 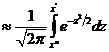 , где
, где 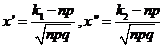 . При решении задач, требующ. применения интегральн. теоремы Лапласа, пользуются специальн. таблицами. В них даны значения функции
. При решении задач, требующ. применения интегральн. теоремы Лапласа, пользуются специальн. таблицами. В них даны значения функции 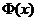 для положит. значений аргумента
для положит. значений аргумента 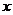 . Для
. Для 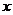 <0 функц.
<0 функц. 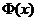 нечетн., т.е.
нечетн., т.е. 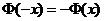 . В табл. приведены значения для
. В табл. приведены значения для 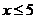 . При
. При 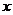 >5 значение функц. считается постоян. и равно 0,5. Для того, чтобы можно было использовать табл. функций Лапл. преобразуем последнюю формулу:
>5 значение функц. считается постоян. и равно 0,5. Для того, чтобы можно было использовать табл. функций Лапл. преобразуем последнюю формулу: 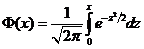 ;
; 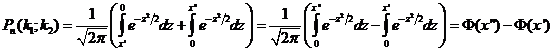 , где
, где 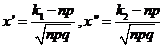 . Вер. того, что соб. А появится в n независим. испытаниях от
. Вер. того, что соб. А появится в n независим. испытаниях от 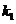 до
до 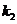 раз равна
раз равна 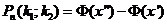 .
.
????Вер. отклонения относит. частоты от постоян. вер. в независим. испытаниях. Будем считать, что производится n независ. испытаний, в кажд. из кот. вер. появл. соб. А постоянна и равна p. Найдем вер. того, что отклонение относит. частоты 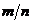 от постоян вер. p по абсолютн. величине не превышает задан. числа
от постоян вер. p по абсолютн. величине не превышает задан. числа 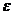 , т.е. найдем вер. осуществления нер-ва:
, т.е. найдем вер. осуществления нер-ва: 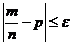 . Заменим дан. нер-во на равносильн. ему нер-во
. Заменим дан. нер-во на равносильн. ему нер-во 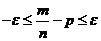 ;
; 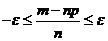 . Умножим последн. нер-во на
. Умножим последн. нер-во на 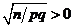 , получим
, получим 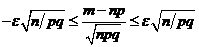 . Воспользуемся интегральн. теоремой Лапл. Положим
. Воспользуемся интегральн. теоремой Лапл. Положим 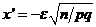 ,а
,а 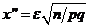 , тогда имеем вер. того, что P(
, тогда имеем вер. того, что P( 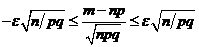 )
) 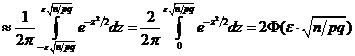 . Окончательно получаем
. Окончательно получаем 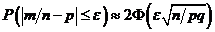 .
.
Формула Пуассона
Если вер. события p в отдельн. испытании близка к 0, то даже при большом числе испытаний n, но небольш. величине 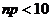 вероятности
вероятности 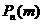 , получен. по локальн. формуле Лапл. не достаточно близки к их истин. значениям. В таких случаях применяют формулу Пуасона. Теор.: Если вер. p наступления соб. А в кажд. испытании постоянна, но близка к 0, число независим. испытаний n достаточн. велико, а
, получен. по локальн. формуле Лапл. не достаточно близки к их истин. значениям. В таких случаях применяют формулу Пуасона. Теор.: Если вер. p наступления соб. А в кажд. испытании постоянна, но близка к 0, число независим. испытаний n достаточн. велико, а 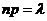 , то вер.
, то вер. 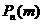 того, что в n независ. испытаниях соб. А наступит m раз
того, что в n независ. испытаниях соб. А наступит m раз 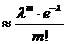 . Это формула Пуасона. Доказ-во: Для вычисления вер.
. Это формула Пуасона. Доказ-во: Для вычисления вер. 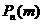 воспользуемся формул. Бернулли:
воспользуемся формул. Бернулли: 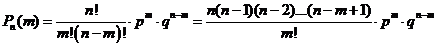 (Т.к.
(Т.к. 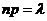 , то
, то 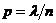 )=
)= 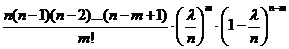 . Т.к. по условию n велико, то найдем предел правой части последн. равенства при
. Т.к. по условию n велико, то найдем предел правой части последн. равенства при 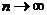 , при этом будет получено приближен. значение вероятн.:
, при этом будет получено приближен. значение вероятн.: 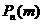 =
= 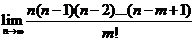
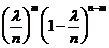 =
= 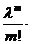
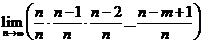
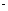
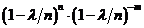 =
= 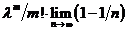
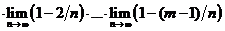
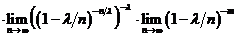 =
= 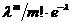 Пределы всех скобок, кроме предпоследн. равны 1 при
Пределы всех скобок, кроме предпоследн. равны 1 при 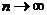 . Следоват-но вер. того, что в n испытаниях событие появится m раз
. Следоват-но вер. того, что в n испытаниях событие появится m раз 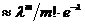 . Замечание: Формулу Пуассона обычно используют, когда
. Замечание: Формулу Пуассона обычно используют, когда 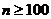 , а
, а 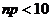 .
.
