Редакционно-издательским Советом ТГСХА в качестве
Редакционно-издательским Советом ТГСХА в качестве
методических указаний
Программа, методические указания и задания для выполнения контрольной работы для студентов заочной формы обучения составлены в соответствии с рабочей программой учебной дисциплины «Математика»
Составители: старший преподаватель кафедры математики Плотникова Т.И.
Научный редактор
Антропов В.А., старший преподаватель, заведующий кафедрой математики
Обсуждено
на заседании кафедры математики
Протокол № 2 от «15» ноября 2006 г.
Одобрено
научно-методическим советом
института экономики и финансов.
Протокол № 3 от «15» ноября 2006 г.
Содержание.
стр.
1. Введение. 4
2. Методика изучения математики в высшем учебном
заведении. 5-10
3. Правила выполнения и оформления контрольных работ. 11-12
4. Программа по высшей математике. Первый курс. 13-16
1 семестр.
5. Литература. 16
6. Методические указания к выполнению контрольной
работы № 1. 17-52
7. Тренировочные задания. 53-55
8. Правило и таблица выбора варианта. 56-58
9. Задания для контрольной работы № 1. 59-68
Введение
Знания, приобретаемые студентом в результате изучения
математики, играют важную роль в процессе его обучения в
институте. Они необходимы для успешного изучения общетеоретических и специальных дисциплин.
В настоящее время математические методы широко используются для решения самых разнообразных технических задач, применяются в экономике и планировании.
Благодаря изучению математики студент приобретает также навыки логического мышления, необходимые каждому специалисту.
Учебные планы экономических специальностей вузов предусматривают три самостоятельных курса:
1.« Высшая математика (общий курс) ».
2.« Теория вероятностей ».
3.« Математическая статистика ».
4.« Эконометрика ».
Объем и содержание этих курсов определяются программами, утвержденными Учебно-методическим управлением по вузам Министерства высшего и среднего специального образования РФ, и не зависят от формы обучения (дневное, вечернее, заочное), но методика изучения их при различных формах обучения различна. Все дополнительные сведения, связанные, например, со спецификой учебных планов или с методикой изучения отдельных вопросов, (последовательность изложения материала и распределение контрольных работ и т.п.), сообщаются студентам кафедрами высшей математики вузов дополнительно к настоящему пособию.
Методика изучения математики в высшем учебном заведении студентами заочниками
Основной формой обучения студента-заочника является самостоятельная работа над учебным материалом по математическим курсам; она складывается из чтения учебников, решения задач, выполнения контрольных заданий. В помощь заочникам институты организуют чтение лекций и практические занятия. Кроме этого студент может обратиться к преподавателю с вопросами для письменной или устной консультации. Указания студенту по текущей работе даются также в процессе рецензирования контрольных работ. Но студент должен помнить, что только при систематической и упорной самостоятельной работе помощь института будет достаточно эффективной.
Завершающим этапом изучения каждого из математических курсов (или отдельных частей общего курса высшей математики) является сдача зачетов и экзаменов в соответствии с учебным планом.
Чтение учебника
1. Изучая материал по учебнику, следует переходить к следующему вопросу только после правильного понимания предыдущего, проделывая на бумаге все вычисления (в том числе и те, которые по их простоте опущены в учебнике), воспроизводя имеющиеся в учебнике чертежи.
2. Особое внимание следует обращать на определения основных понятий курса, которые отражают количественную сторону или пространственные свойства реальных объектов и процессов и возникают в результате абстракции из этих свойств и процессов. Без этого невозможно успешное изучение математики.
Студент должен подробно разбирать примеры, которые
поясняют такие определения. И уметь строить аналогичные примеры самостоятельно.
3. Необходимо помнить, что каждая теорема состоит из предположений и утверждений. Все предположения должны обязательно использоваться в доказательстве. Нужно добиваться точного представления о том, в каком месте доказательства использовано каждое предположение теоремы. Полезно составлять схемы доказательства сложных теорем. Правильному пониманию многих теорем помогает разбор примеров математических объектов, обладающих или не обладающих свойствами, указанными в предположениях и утверждениях теорем.
4. При изучении материала по учебнику полезно вести конспект, в который рекомендуется выписывать определения, формулировки теорем, формулы, уравнения и т. п.
На полях конспекта следует отмечать вопросы, выделенные студентом для письменной или устной консультации с преподавателем.
5. Письменное оформление работы студента имеет исключительно важное значение. Записи в конспекте должны быть сделаны чисто, аккуратно и расположены по порядку. Хорошее внешнее оформление конспекта по изученному материалу не только приучит студента к необходимому в работе порядку, но и позволит ему избежать многочисленных ошибок, которые происходят из-за небрежных, беспорядочных записей
6. Выводы, полученные в виде формул, рекомендуется в конспекте подчеркивать или обводить рамкой. Чтобы при перечитывании конспекта они выделялись и лучше запомнились. Опыт показывает, что многим студентам помогает в работе составление листа, содержащего важнейшие и наиболее часто употребляемые формулы курса. Такой лист не только помогает запомнить формулы, но и может служить постоянным справочником для студента.
Решение задач
1. Чтение учебника должно сопровождаться решением задач, для чего рекомендуется завести специальную тетрадь.
2. При решении задач нужно обосновать каждый этап решения, исходя из теоретических положений курса. Если студент видит несколько путей для решения задачи, то он должен сравнить их и выбрать из них самый удобный.
Полезно до начала вычислений составить краткий план решения задачи.
3. Решения задач и примеров следует излагать подробно, вычисления должны располагаться в строгом порядке, при этом рекомендуется отделять вспомогательные вычисления от основных. Ошибочные записи следует не стирать и не замазывать, а зачеркнуть.
Чертежи можно выполнять от руки, но аккуратно и в соответствии с данными условиями. Если чертеж требует особо тщательного выполнения, например при графической проверке решения, полученного путем вычислений, то следует пользоваться линейкой, транспортиром, лекалом и указывать масштаб.
4. Решение каждой задачи должно доводиться до окончательного ответа, которого требует условие, и, по возможности, в общем виде с выводом формулы. Затем в полученную формулу подставляют числовые значения (если таковые даны) входящих в нее букв. В промежуточных вычислениях не следует вводить приближенные значения корней.
5. Полученный ответ следует проверять способами, вытекающими из существа данной задачи. Если, например, решалась задача с конкретным физическим или геометрическим содержанием, то полезно прежде всего проверить размерность полученного ответа.
Полезно также, если возможно, решить задачу несколькими способами и сравнить полученные результаты.
6. Решение задач определенного типа нужно продолжать до приобретения твердых навыков в их решении.
Самопроверка
1. После изучения определенной темы по учебнику и решения достаточного количества соответствующих задач студенту рекомендуется воспроизвести по памяти определения, выводы формул, формулировки и доказательства теорем, проверяя себя каждый раз по учебнику.
Вопросы для самопроверки, приведенные в настоящем пособии, имеют целью помочь студенту в таком повторении, закреплении и проверке прочности усвоения изученного материала.
В случае необходимости надо еще раз внимательно разобраться в материале учебника, прорешать задачи.
2. Иногда недостаточность усвоения того или иного вопроса выясняется только при изучении дальнейшего материала. В этом случае надо вернуться назад и повторить плохо усвоенный раздел.
3. Важным критерием усвоения теории является умение решать задачи на пройденный материал. Однако здесь следует предостеречь студента от весьма распространенной ошибки, заключающейся в том, что благополучное решение задач воспринимается им как признак усвоения теории. Часто правильное решение задачи получается в результате применения механически заученных формул, без понимания существа дела. Можно сказать, что умение решать задачи является необходимым, но недостаточным условием хорошего знания теории.
Консультации
1. Если в процессе работы над изучением теоретического материала или при решении задач у студента возникают вопросы, разрешить которые самостоятельно не удается (неясность терминов, формулировок теорем, отдельных задач и др.), он может обратиться к преподавателю для получения от него указаний в виде письменной или устной консультаций.
2. В своих запросах студент должен точно указывать, в чем он испытывает затруднение. Если он не разобрался в теоретических объяснениях или в доказательстве теоремы, или в выводе формулы по учебнику, то нужно указать, какой это учебник, год его издания и страницу, где рассмотрен затрудняющий его вопрос, и что именно его затрудняет. Если студент испытывает затруднение при решении задачи, то следует указать характер этого затруднения, привести предполагаемый план решения.
З. За консультацией следует обращаться и в случае, если возникнут сомнения в правильности ответов на вопросы для самопроверки.
Контрольные работы
1. В процессе изучения математических курсов студент должен выполнить ряд контрольных работ, главная цель которых- оказать студенту помощь в его работе. Рецензии на эти работы позволяют студенту судить о степени усвоения им соответствующего раздела курса; указывают на имеющиеся у него пробелы, на желательное направление дальнейшей работы; помогают сформулировать вопросы для консультации с преподавателем (письменной или устной ).
2. Не следует приступать к выполнению контрольного задания до решения достаточного количества задач по материалу, соответствующему этому заданию. Опыт показывает, что чаще всего неумение решить ту или иную задачу контрольного задания вызывается тем, что студент не выполнил это требование.
3.Контрольные работы должны выполняться самостоятельно. Несамостоятельно выполненная работа не дает возможности преподавателю-рецензенту указать студенту на недостатки в его работе, в усвоении им учебного материала, в результате чего студент не приобретает необходимых знаний и может оказаться не подготовленным к устному экзамену и зачету.
4.Не рекомендуется присылать в институт одновременно несколько работ - это не дает возможности рецензенту своевременно указать студенту на допускаемые им ошибки и удлиняет срок рецензирования работ.
5.Прорецензированные контрольные работы вместе со всеми исправлениями и дополнениями, сделанными по требованию рецензента, следует сохранять. Без предъявления преподавателю прорецензированных контрольных работ студент не допускается к сдаче зачета или экзамена.
За первый курс.
I семестр.
V. Интегральное исчисление
19.Понятие первообразной; неопределенного интеграла. Таблица основных интегралов. Методы интегрирования: непосредственное, замена переменной, по частям. Интегрирование рациональных дробей.
20.3адачи, приводящие к понятию определенного интеграла. Понятие определенного интеграла, как предела интегральных сумм. Теорема существования. Свойства определенного интеграла. Связь определенного интеграла с неопределенным. Формула Ньютона-Лейбница. Методы интегрирования для определенного интеграла. Приложение определенного интеграла к решению задач.
21. Понятие несобственных интегралов с бесконечными пределами интегрирования и от неограниченных функций. Понятие сходящихся и расходящихся интегралов. Интеграл Пуассона. Геометрический смысл сходящихся несобственных интегралов.
Литература
1. Высшая математика для экономистов. Под редакцией проф. Н. Ш. Крамера. – М.: Юнити, 2001
2. Баврин. И. И. Высшая математика. М.: Академия, 2002
3. Зайцев И. А. Высшая математика. Учебное пособие для неинженерных специальностей с.-х. Вузов. – М.: Высшая школа, 1991
4.Шипачев В. С. Высшая математика– М.: Высшая школа, 1996
5. Лихолетов И. И. Высшая математика, теория вероятностей и математическая статистика. Минск. Высшая школа, 1976
6. Карасев А. И., Аксютина З. М., Савельева Т. И. . Высшая математика для экономических ВУЗов – ч. 1 – М.: Высшая школа, 1982
7. Минорский В. П. сборник задач по высшей математике. –М.: Наука, 1987
8. Данко П. Е., Попов А. Г.- ч. 1,2 - М.: Высшая школа, 1974
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
КОНТРОЛЬНАЯ РАБОТА №1
Первая контрольная работа посвящена темам: «Аналитическая геометрия на плоскости», «Введение в математический анализ»,
«Дифференциальное исчисление функции одной переменной», «Дифференциальное исчисление функции с двумя переменными», «Интегральное исчисление».
Задачи 1-10
Предварительно ознакомьтесь со следующими вопросами по теме «Аналитическая геометрия на плоскости»:
1. Метод координат на плоскости. Расстояние между двумя точками на плоскости А(х1;у1) и В(х2;у2):
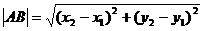
2. Деление отрезка пополам (нахождение середины отрезка):
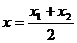 ;
; 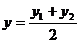
3. Угловой коэффициент прямой: k = tgα, где α- угол наклона прямой к оси ОХ, 0 ≤ α < π
4. Уравнение прямой с угловым коэффициентом: у = kx+b.
5. Уравнение прямой, проходящей через заданную точку (хо;уо) в данном направлении (уравнение пучка прямых):
у - уо = k (х - хо).
6. Уравнение прямой, проходящей через две заданные точки (х1;у1) и (х2;у2): 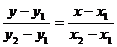
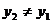 ,
, 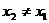
7. Общее уравнение прямой Ах + By + С = 0, его частные случаи: Ах+Ву=0, Ах+В=0, Ву+С=0.
8. Угол между двумя прямыми:
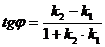
где k1 и k2 - угловые коэффициенты данных прямых.
9. Условие параллельности двух прямых: k1 =k2.
10. Условие перпендикулярности двух прямых:
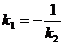
11. Расстояние от точки 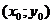 до прямой
до прямой 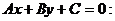
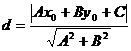
Обратите внимание, что уравнение прямой, в каком бы виде оно ни было записано, является уравнением первой степени.
Задача. Даны вершины треугольника А(2;1), В(-4;4), С(-1,5). Сделать чертеж и найти:
1) длину стороны АВ;
2) внутренний угол А в радианах с точностью до 0,001;
3) уравнение высоты CD, проведенной через вершину С;
4) уравнение медианы BE, проведенной через вершину В;
5) точку пересечения высоты CD и медианы BE;
6) длину высоты, опущенной из вершины С.
Решение. Начнем решение задачи с выполнения чертежа (рис 1).
Построим точки А(2;1), В(-4;4), С(-1;5) в прямоугольной системе координат и, соединив их отрезками прямых, получим треугольник ABC. Проведем высоту CD и медиану BE, уравнения которых нужно найти.
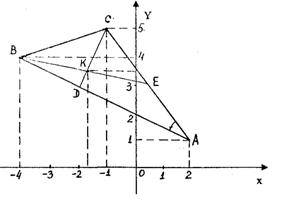
Рис. 1
1. Длину стороны АВ находим как расстояние между двумя точками А(2;1) и В(-4;4) по формуле:
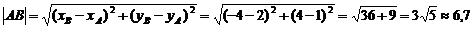 2. При ответе на вопрос пункта 2 (найти внутренний угол) воспользуемся чертежом. Отметим искомый угол А дугой и на ней поставим стрелку, показывающую направление, противоположное движению часовой стрелки. Первой будет та прямая, от которой, направлена стрелка. Так, на рис. 1 первая прямая АС, вторая - АВ.
2. При ответе на вопрос пункта 2 (найти внутренний угол) воспользуемся чертежом. Отметим искомый угол А дугой и на ней поставим стрелку, показывающую направление, противоположное движению часовой стрелки. Первой будет та прямая, от которой, направлена стрелка. Так, на рис. 1 первая прямая АС, вторая - АВ.
Следовательно, в формуле надо положить 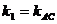 и
и 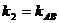
Найдем указанные угловые коэффициенты прямых. Для этого нет необходимости составлять их уравнения, проще воспользоваться формулой, где угловой коэффициент прямой находится по координатам двух ее точек.
Так, в нашем примере:
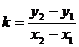
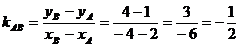
тогда
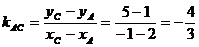
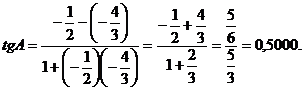
Заметим что tg A > 0, так как угол А - острый.
Из таблицы (например, Брадиса) видно, что такое значение тангенса соответствует углу А=26°34/.
Обратите внимание на то, что ответ следует дать в радианах. Для перевода градусов в радианы можно воспользоваться соответствующими таблицами, либо формулой:
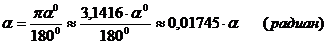
α - угол в градусах.
Итак, в радианах угол 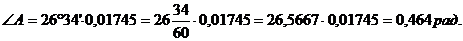 3. Составим уравнение высоты CD. Высота CD перпендикулярна стороне АВ. Угловой коэффициент прямой АВ был найден ранее:
3. Составим уравнение высоты CD. Высота CD перпендикулярна стороне АВ. Угловой коэффициент прямой АВ был найден ранее:
kAВ = -1/2
По условию перпендикулярности двух прямых
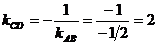
Уравнение высоты СD cоставим по известной точке С (-1;5)
найденному угловому коэффициенту, воспользовавшись урав-
нением 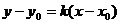 ; пучка прямых:
; пучка прямых: 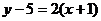 .
.
Ответ обычно дают в виде уравнения с целыми коэффициентами и с правой частью, равной нулю. Преобразуем полученное уравнение:
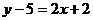 ;
; 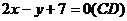
Замечание. Возьмите себе за правило проверять полученные результаты, причем это следует делать не простым повторением проделанных действий, а каким-либо другим способом. Например, полученное уравнение высоты СD проверьте, подставив в него координаты точки С, при этом должно получиться тождество.
Действительно: 2 (- 1) – 5 + 7 = 0.
4. Уравнение медианы ВЕ, проведенной из вершины В, составляется по координатам двух точек В и Е. Координаты точки В известны, а координаты точки Е находим как координаты середины отрезка АС по формулам деления отрезка пополам: 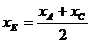 ;
; 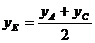
В рассматриваемой задаче
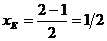 ;
; 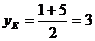
Имея две точки В(-4;4) и Е (1/2;3) Запишем уравнение ВЕ:
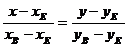
а именно: 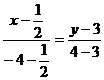 ;
; 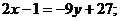
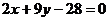 (BE)
(BE)
5. Координаты точки пересечения высоты СD и медианы ВЕ найдем, решив систему уравнений СD и ВЕ:
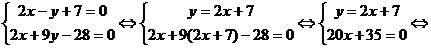
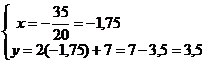
Итак, К(-1,75; 3,5), что соответствует чертежу на рис. 1.
б.Длина высоты СD есть расстояние от вершины С до стороны АВ. Поэтому длину высоты находим по формуле расстояния от точки 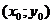 до прямой
до прямой 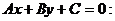
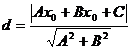
В данной задаче С (-1;5), а уравнение стороны АВ можно составить, используя уравнение пучка прямых:
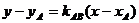 , где
, где 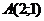 и
и 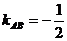
Тогда
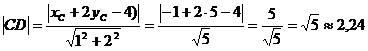
Задачи 11-20
Предварительно ознакомьтесь со следующими вопросами по теме «Кривые второго порядка»
1. Что называется кривой второго порядка?
2. Канонические уравнения кривых второго порядка. Графики этих кривых:
а) окружность: 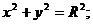
б) эллипс: 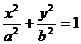 ;
;
в) гипербола: 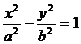 ;
;
г) парабола: 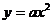 (с осью симметрии Оу),
(с осью симметрии Оу),
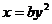 (с осью симметрии Ох).
(с осью симметрии Ох).
З. Параллельный перенос системы координат. Приведение уравнения второго порядка к каноническому виду.
Указанные виды кривых исчерпывают все виды кривых второго порядка (исключая случаи вырождения).
В результате решения задачи вы должны получить одну из названных кривых и построить ее в прямоугольной системе координат.
Задача. Составить уравнение линии, для каждой точки которой отношение расстояний до точки F(5;0) и до прямой 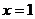 равно
равно 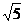 .
.
Решение. Построим в системе координат точку F(5;0) и вертикальную прямую Х=1(рис.2).
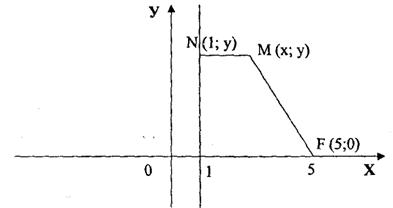
Рис.2.
Пусть М (х,у) - произвольная (текущая) точка искомой линии.
На рис. 2 изображены расстояния от этой точки до заданной точки F, то есть MF, и до заданной прямой: х=1, то есть MN. Обратите внимание, что MN - перпендикуляр к заданной прямой и поэтому точка N имеет (как и точка М) ординату, равную у: N(1 ;у).
По условию задачи 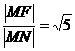
Выразим длины отрезков MF и MN через координаты их концов по формуле расстояния между точками:
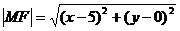 ;
;
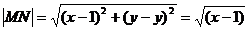
Тогда по условию
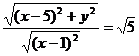

Это и есть уравнение искомой линии. Упростим его, возведя в квадрат обе части уравнения и сделав другие преобразования: 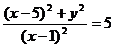 ;
; 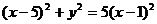 ;
; 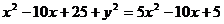 ;
; 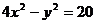
Разделим обе части уравнения на 20: 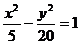
Это каноническое уравнение гиперболы. Из него видно, что действительная полуось гиперболы 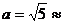 2,25, мнимая полуось
2,25, мнимая полуось 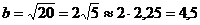 .
.
Центр симметрии гиперболы находится в начале координат. Для построения гиперболы отложим на осях координат в обе стороны от начала координат полуоси гиперболы 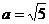 и
и 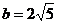 .
.
Через полученные точки «-а» и «а» на оси Ох и точки «-b» и «b» на оси Оу построим вспомогательный прямоугольник (рис. 3). Проведем диагонали этого прямоугольника, которые являются асимптотами гиперболы: к ним будут неограниченно приближаться ветви гиперболы, Построим кривую, как указано на рис. 3. Задача решена.
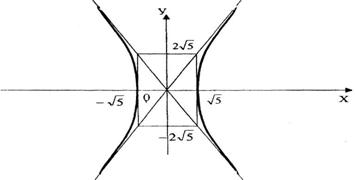
Рис. 3
Замечание. Если бы в этой задаче после преобразований вы получили уравнение
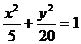
, то оно определяет эллипс, порядок построения которого ясен из рис.4.
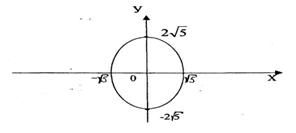
Рис.4
Замечание. Если в задаче вашего варианта после преобразований в уравнении наряду с членами 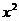 и
и 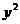 присутствуют члены, содержащие первые степени
присутствуют члены, содержащие первые степени 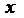 или
или 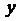 , то следует выделить полный квадрат (соответственно по
, то следует выделить полный квадрат (соответственно по 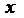 или по
или по 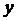 ).
).
Например, в уравнении 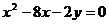 выделим полный квадрат по
выделим полный квадрат по 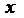 , для чего прибавим и отнимем половину коэффициента при
, для чего прибавим и отнимем половину коэффициента при 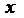 , возведенную в квадрат:
, возведенную в квадрат:
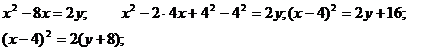 Обозначим
Обозначим 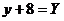 ;
; 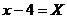 , тогда
, тогда 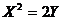 или
или 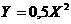 - это каноническое уравнение параболы.
- это каноническое уравнение параболы.
Построим новые оси 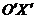 и
и 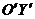 , которые смещены относительно старых осей
, которые смещены относительно старых осей 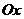 и
и 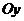 так, что новое начало координат будет находиться в точке
так, что новое начало координат будет находиться в точке 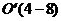 , где и расположена вершина параболы. Ось симметрии параболы
, где и расположена вершина параболы. Ось симметрии параболы 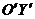 , ветви ее направлены вверх, так как коэффициент при
, ветви ее направлены вверх, так как коэффициент при 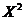 положительный.
положительный.
Полезно найти точки пересечения параболы 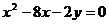 со старыми осями координат
со старыми осями координат 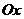 и
и 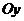 .
.
При 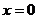 получим
получим 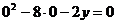 , откуда
, откуда 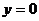 , таким образом, парабола проходит через точку
, таким образом, парабола проходит через точку 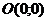 - в старой системе координат.
- в старой системе координат.
| |
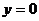 получаем уравнение
получаем уравнение 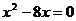 , откуда
, откуда 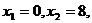 т.е. парабола пересекает ось
т.е. парабола пересекает ось 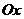 в точках
в точках 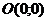 и (8;0) (рис.5)
и (8;0) (рис.5) | |
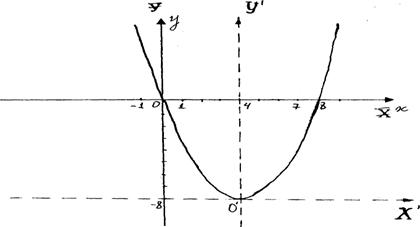
Рис.5
Задачи 21-30
 По теме «Введение в анализ» рассмотрите предварительно следующие вопросы о функциях и пределах:
По теме «Введение в анализ» рассмотрите предварительно следующие вопросы о функциях и пределах:
1. Понятие функции, способы задания функции, область ее определения.
2. Основные элементарные функции, их свойства и графики.
3. Понятие предела функции в точке.
4. Понятие бесконечно малой функции 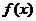 и ее свойства:
и ее свойства: 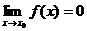
5. Понятие бесконечно большой функции 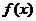 :
:
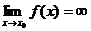
ее свойства и связь с бесконечно малой функцией.
6. Теоремы о пределах: предел суммы, разности, произведения, частного функций.
7.Первый замечательный предел:
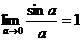 или
или 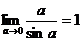
8. Второй замечательный предел:
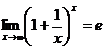
или в другой форме:

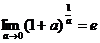
где e- иррациональное число: 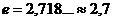 .
.
9. Эквивалентные бесконечно малые функции.
10. Виды неопределенностей и способы их раскрытия:
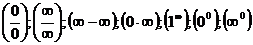
11. Понятие непрерывности функции в точке и на промежутке.
12. Теоремы о непрерывных функциях.
Задача. Найти пределы функций:
1. 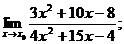 2.
2. 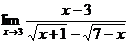

При 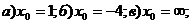
3. 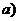
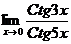
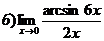
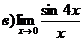 4.
4. 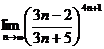
Решение. Прежде всего заметим, что во всех примерах следует найти предел частного. Как известно, предел частного существует и равен частному пределов, если существуют пределы числителя и знаменателя и предел знаменателя не равен нулю.
1.а) 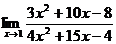
Предел числителя и предел знаменателя дроби найдем, подставив в них предельное значение аргумента:
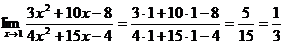
Здесь теорема о пределе частного применима.
б) 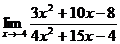
При подстановке 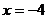 в числитель и знаменатель дроби убеждаемся, что их пределы равны нулю. Теорема о пределе частного здесь не применима. В данном случае говорят, что имеется неопределенность вида «ноль на ноль»
в числитель и знаменатель дроби убеждаемся, что их пределы равны нулю. Теорема о пределе частного здесь не применима. В данном случае говорят, что имеется неопределенность вида «ноль на ноль» 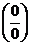
Такая неопределенность раскрывается сокращением дроби на бесконечно малую функцию 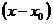 , в данном случае на
, в данном случае на 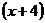 , которая обращает числитель и знаменатель в нуль. Для этого нужно сначала разложить на множители числитель и знаменатель дроби.
, которая обращает числитель и знаменатель в нуль. Для этого нужно сначала разложить на множители числитель и знаменатель дроби.
Напомним формулу разложения квадратного трехчлена на множители: 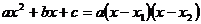 , где
, где 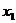 и
и 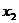 -корни квадратного трех-
-корни квадратного трех-
члена, которые находим из уравнения 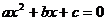 .
.
Разложим на множители числитель данной дроби:
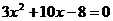 ;
; 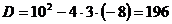
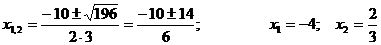
Следовательно: 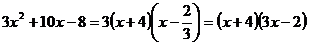
Разложим на множители знаменатель дроби:
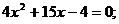
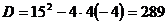 ;
;
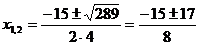
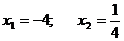
Следовательно: 4х2+15х-4=4(х+4)(х-1 /4)=(х+4)(4х-1).
Тогда 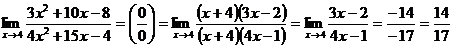 в)
в) 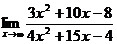
При 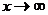 числитель и знаменатель дроби также стремятся к бесконечности. В этом случае теорема о пределе частного неприменима. Говорят, что имеется неопределенность вида «бесконечность на бесконечность»
числитель и знаменатель дроби также стремятся к бесконечности. В этом случае теорема о пределе частного неприменима. Говорят, что имеется неопределенность вида «бесконечность на бесконечность» 
Чтобы ее раскрыть, каждый член числителя и знаменателя дроби разделим на 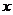 в наивысшей для данного примера степени (то есть на
в наивысшей для данного примера степени (то есть на 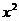 ), от чего величина дроби не изменится. Тогда получим:
), от чего величина дроби не изменится. Тогда получим:
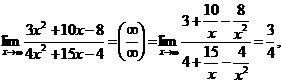
так как 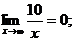
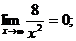
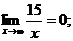
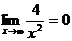
Замечание. Полезно заметить и запомнить, что предел отношения многочленов при 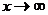 равен отношению их коэффициентов при старших степенях.
равен отношению их коэффициентов при старших степенях.
2. 
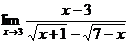
При подстановке предельного значения 
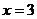 в числитель и знаменатель дроби убеждаемся, что их пределы равны нулю. Таким образом, перед нами вновь неопределенность вида
в числитель и знаменатель дроби убеждаемся, что их пределы равны нулю. Таким образом, перед нами вновь неопределенность вида
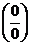
которая раскрывается сокращением дроби на бесконечно малую функцию 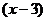 . Для этого предварительно умножим числитель и знаменатель дроби на выражение, сопряженное иррациональному выражению в знаменателе, то есть на
. Для этого предварительно умножим числитель и знаменатель дроби на выражение, сопряженное иррациональному выражению в знаменателе, то есть на 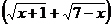 :
:
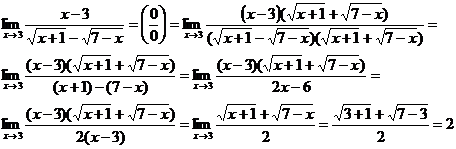
При умножении сопряженных выражений в знаменателе было использовано тождество 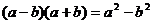
З.Для решения примеров под номером 3 используется первый замечательный предел, с помощью которого раскрываются некоторые неопределенности вида 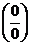
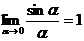
Примеры этого пункта можно решать также с помощью эквивалентных бесконечно малых функций. Две бесконечно малые функции 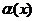 и
и 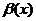 называются эквивалентными в точке
называются эквивалентными в точке 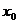 , если предел их отношения в этой точке равен 1:
, если предел их отношения в этой точке равен 1:
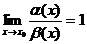
значит 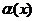 ~
~ 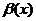 при
при 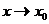
Например, при 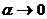 :
: 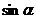 ~
~ 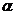 ;
; 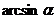 ~
~ 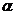 ;
;
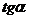 ~
~ 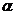 ;
; 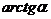 ~
~ 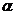 .
.
При вычислении пределов бесконечно малые множители можно заменять на эквивалентные им.
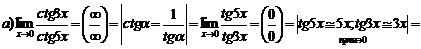
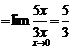

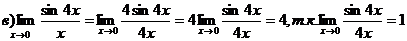
4.Для раскрытия неопределенностей вида ( 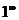 ) применяется второй замечательный предел:
) применяется второй замечательный предел:
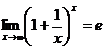
где e - иррациональное число, то есть бесконечная непериодическая десятичная дробь, ее приближенное значение: e ≈ 2,7
Найдем 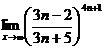
Очевидно, что 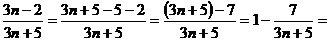
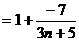
Тогда
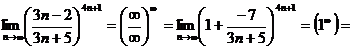
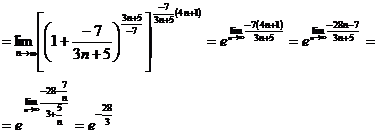
Задачи 31-40,41-50,51-60
 Названные задачи относятся к теме «Дифференциальное исчисление и его приложения». Основные вопросы этой темы:
Названные задачи относятся к теме «Дифференциальное исчисление и его приложения». Основные вопросы этой темы:
1. Понятие производной, ее геометрический и механический смысл.
2. Правила дифференцирования суммы, разности, произведения, частного и суперпозиции функций.
3. Формулы дифференцирования основных элементарных функций (таблица производных).
4. Дифференциал функции, его геометрический смысл. Применение дифференциала в приближенных вычислениях.
5. Признаки возрастания и убывания для функции одной переменной.
6. Экстремумы функции одной переменной. Необходимое и достаточное условия существования экстрем
