Метод: первый замечательный предел.
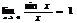
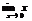 ~
~ 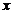 ;
; 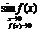 ~
~ 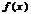
4-метод: 2-ой замечательный предел.
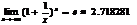
Если обозначить 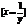
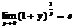 .
.
Пр. 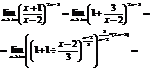
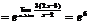 .
.
Производная и дифференциал функции. Правило дифференцирования.
Производной 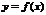 в точке
в точке 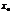 наз-тся
наз-тся 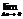 отношения приращения ф. к приращению аргумента если этот предел сущ-ет.
отношения приращения ф. к приращению аргумента если этот предел сущ-ет. 
Геом. смысл производной: угловой коэф. касательной в точке 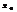 = значению производной в этой точке.
= значению производной в этой точке. 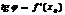
О. Ф. 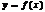 наз-тся дифференцируемой в точке
наз-тся дифференцируемой в точке 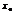 , если она имеет в этой точке конечную производную. Если ф. дифференцируема в каждой точке интервала
, если она имеет в этой точке конечную производную. Если ф. дифференцируема в каждой точке интервала 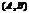 , то она наз-тсядифференцируемой на
, то она наз-тсядифференцируемой на 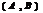 .
.
Если ф. дифференцируема в т. 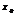 , то
, то 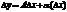 , где
, где 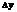 –приращение ф. ,
–приращение ф. , 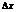 -приращение аргумента. А-число не зависящее от
-приращение аргумента. А-число не зависящее от 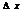 ;
; 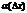 -бесконечно малое, при
-бесконечно малое, при 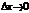
Дифференциалом ф. 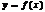 в точке
в точке 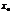 наз-тся линейная часть ур-ния
наз-тся линейная часть ур-ния 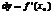
Дифференциалом независимой переменной 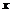 наз-тся приращение этой переменной, т.е.
наз-тся приращение этой переменной, т.е. 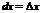 . Т.о.
. Т.о. 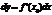
Т. Если ф. 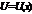 и
и 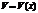 диф. в т.
диф. в т. 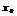 , то их сумма, разность, произведение и частное также диф-мы в этой точке. Причем:
, то их сумма, разность, произведение и частное также диф-мы в этой точке. Причем: 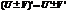 ,
, 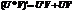 ,
, 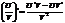 .
.
Т.Если функция х=Р(t) имеет производную в т.t0,а функция у=f(x)имеет производную в соответствующей точке x0=P(t0),то сложная функция f(P(t))=имеет производную в т. t0
Производная 1-го порядка: функция 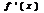
Производная второго порядка- производная от 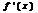
Дифференциал 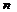 –ного порядка
–ного порядка 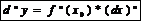
13)Основные теоремы дифференциального исчисления.
Теорема Ферма.
ф-я 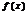 определена на
определена на 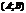 и в нек-рой точке
и в нек-рой точке 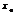 этого интервала имеет наиб.или наим. значение, тогда если в этой точке определена производная, то она =0, т.е.
этого интервала имеет наиб.или наим. значение, тогда если в этой точке определена производная, то она =0, т.е. 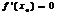
Если произв. в точке 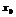 =0, будет ли в этой точке наиб.или наим. значение.
=0, будет ли в этой точке наиб.или наим. значение.
Док-во:
Пусть для определенности в т.х0 наибольшее значение,т.е. для любого х принадлежашего (а;b)
f(x)  f(x0);f(x)-f(x0)
f(x0);f(x)-f(x0)  0следовательно дельта у
0следовательно дельта у  0,пусть дельта х больше 0(предел с права);предел при дельта х стремящемся к 0 (дельта у/дельта х)
0,пусть дельта х больше 0(предел с права);предел при дельта х стремящемся к 0 (дельта у/дельта х)  0,если дельта х
0,если дельта х  0,то предел больше 0
0,то предел больше 0
Пр. 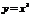 в точке 0 производная =0.
в точке 0 производная =0.
Теорема Ролля.
Пусть на отрезке 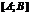 определена ф-я
определена ф-я 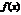 , причем:
, причем:
ü 
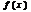 непрерывна на
непрерывна на 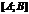
ü 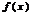 дифференцируема на
дифференцируема на 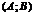
ü 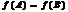
Тогда сущ-ет точка 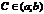 , что
, что 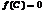
Док-во:
Т.к функция непрерывна на отрезке [a;b] то по 2 теореме Вейерштрасса она имеет на этом отрезке наибольшее значение М и наименьшее m,т.е. существуют такие точки x1и x2принадлежащие [a;b],что f(x1)=m,f(x2)=M и выполняется m  f(x)
f(x)  M,для любого х принадлежащего отрезку.
M,для любого х принадлежащего отрезку.
1)m=Mтогда f(x)=const и f’(x)=0
2)m  M,т.кf(a)=f(b),то хотя бы одно из значений наибоьшее или наименьшее достигается на интервале (a;b),т.е. существует т.С принадлежащая(a;b)в кот. Функция имеет наиб.илинаим. Значение т.к. функция дифериенцируема в тС
M,т.кf(a)=f(b),то хотя бы одно из значений наибоьшее или наименьшее достигается на интервале (a;b),т.е. существует т.С принадлежащая(a;b)в кот. Функция имеет наиб.илинаим. Значение т.к. функция дифериенцируема в тС
f’(C)=0,по теореме ферма..
Теорема Лагранжа.
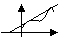 Пусть на
Пусть на 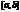 определена ф-я
определена ф-я 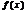 причем:
причем:
ü 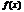 непрерывна на
непрерывна на 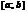
ü 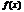 диффер. на
диффер. на 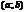
Тогда сущ-ет точка С, принадлежащ. 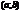 , такая, что
, такая, что 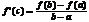
Док-во:
Введем в рассмотрение функцию F(x),для функции выполняется:1)F(x) не преывна на отрезке [a;b],как сумма не прерывных функции.2)F(x) ифференцируема на на интервале (a;b) как сумма дифференцируемых функции.3)F(a)=F(b)=0 следовательно существует такая т.С принадлежащая (a;b),что F’(C)=0,следовательно F’(C)= 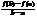
Теорема Коши.
Пусть 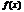 и
и 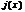 непрерывны на
непрерывны на 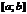 и дифференцируемы на
и дифференцируемы на 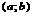 и пусть кроме того
и пусть кроме того 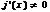 , тогда сущ-ет
, тогда сущ-ет 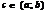 такая, что
такая, что 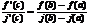 . Если в кач-ве
. Если в кач-ве 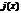 взять ф-ю.
взять ф-ю. 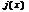 =
= 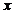 , то получим т. Лагранжа. Если т. Лагранжа положить
, то получим т. Лагранжа. Если т. Лагранжа положить 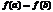 , то получим т. Коши.
, то получим т. Коши.
Теорема Лапиталля-Бернулли.
Пусть 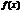 и
и 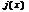 определены и дифф. на
определены и дифф. на 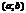 содержащим точку
содержащим точку 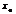 за исключением быть может самой точки
за исключением быть может самой точки 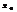 . Пусть предел при
. Пусть предел при 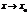 и
и 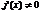 на
на 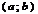 , тогда если сущ-ет конечный предел, при,
, тогда если сущ-ет конечный предел, при, 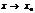
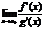 то сущ-ет и
то сущ-ет и 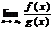 причем они равны
причем они равны
14)Исследование поведения ф-и и построение её графика.
Признак и ¯.
О. Ф-я 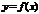 на
на 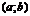 наз-тся : 1)постоянной, если
наз-тся : 1)постоянной, если 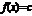 , где
, где 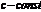 для
для 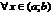 ;2)возрастающей, если для любых двух значений
;2)возрастающей, если для любых двух значений 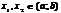 , таких что
, таких что 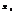 <
< 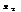 вып-тсянер-во
вып-тсянер-во 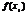 <
< 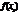 ; 3)убывающей, если из
; 3)убывающей, если из 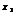 <
< 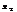 следует
следует 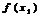 >
> 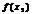
Достаточное условие и ¯ функции.
Если в данном промежутке 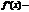 «+», то ф-я в этом промежутке, если
«+», то ф-я в этом промежутке, если 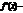 «-», то ф-я ¯. Если же на промежутке
«-», то ф-я ¯. Если же на промежутке 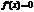 , то ф-я постоянна на этом промежутке.
, то ф-я постоянна на этом промежутке.
Док-во:
Рассмотрим функцию у= f(x) на интервале(а;b) рассмотрим произвольные х1 и х2,такие что х1  ч2,по теоремк Лагранжа сущт.С принадлежащая(х1;х2),такая ,что f(x2)- f(x1)=f’(c)(х2-х1);преположим,что производная на (а$b) положительна тогда f(x2)больше f(x1),соответственно если отриц.томеньше,если =0 то раны.В силу произвольности х1 и х2 функция fя вляетсяпостояннлй
ч2,по теоремк Лагранжа сущт.С принадлежащая(х1;х2),такая ,что f(x2)- f(x1)=f’(c)(х2-х1);преположим,что производная на (а$b) положительна тогда f(x2)больше f(x1),соответственно если отриц.томеньше,если =0 то раны.В силу произвольности х1 и х2 функция fя вляетсяпостояннлй
Экстремумы ф-и.
Рассм. нек-рую ф-ю 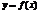 , определенную на
, определенную на 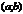 . Пусть
. Пусть 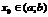 , d–нек-рое «+» число, d-окрестностью в точке
, d–нек-рое «+» число, d-окрестностью в точке 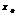 будем наз-ть интервал
будем наз-ть интервал 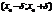 и обозначать
и обозначать 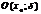 .
.
О. Если можно указать такую d–окрестность 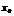 , принадлежащую
, принадлежащую 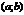 , что для всех
, что для всех 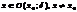 вып-тся
вып-тся 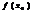 >
> 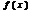 , то
, то 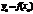 наз-ют максимумом ф-и
наз-ют максимумом ф-и 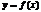 и обозначают
и обозначают 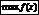 . Если же вып-тсянер-во , то минимумом –
. Если же вып-тсянер-во , то минимумом – 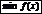
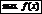 и
и 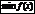 наз-ют экстремумом. Значение аргумента, при к-ром достигается экстремум, наз-ют точкой экстремума.
наз-ют экстремумом. Значение аргумента, при к-ром достигается экстремум, наз-ют точкой экстремума.
Т. (необходимое условие экстремума). В точке экстремума дифф. ф-и ее производная =0.
Если производная =0, то отсюда не следует, что 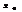 -точка экстремума.
-точка экстремума.
О. Точка, в к-рой производная =0 наз-тсястационарной. Точки, в к-рых произв. =0, а также точки, в к-рых производная не существует, либо =¥наз-ют критическими точками. Т.о. точки экстремума следует искать среди критических точек.
Т.(достаточное условие экстремума). Пусть ф-я 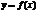 дифференцируема в нек-рой окрестности
дифференцируема в нек-рой окрестности 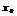 . Если в точке
. Если в точке 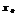 производная=0 и меняет знак при переходе через
производная=0 и меняет знак при переходе через 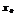 , то
, то 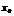 –точка экстремума, причем : 1)если произв. меняет знак с – на + это точка минимума; 2)с + на – точка максимума.
–точка экстремума, причем : 1)если произв. меняет знак с – на + это точка минимума; 2)с + на – точка максимума.
Т.Если в точке 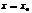 1-ая произв. дифф-мая. в нек-рой окрестности
1-ая произв. дифф-мая. в нек-рой окрестности 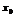 ф-и =0, а 2-ая произв. отлична от нуля, то
ф-и =0, а 2-ая произв. отлична от нуля, то 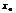 явл. точкой экстремума. Причем
явл. точкой экстремума. Причем 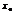 -
- 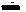 если
если 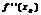 >0, и
>0, и 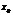 -
- 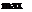 если
если 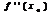 <0.
<0.
Направление выпуклости и точки перегиба.
О. График 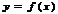 наз-тсявыпуклым вниз в данном промежутке, если он целеком расположен выше касательной в его производной точке и выпуклым вверх-если расположен ниже касательной.
наз-тсявыпуклым вниз в данном промежутке, если он целеком расположен выше касательной в его производной точке и выпуклым вверх-если расположен ниже касательной.
Т. Достаточный признак выпуклости графика ф-и.
Если 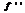 ф-и –«+» в данном промежутке, то график ф. явл. выпуклым вниз в данном промежутке. Если же
ф-и –«+» в данном промежутке, то график ф. явл. выпуклым вниз в данном промежутке. Если же 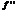 –«-«, то-выпуклым вверх.
–«-«, то-выпуклым вверх.
О. Точка, в к-рой меняется направление выпуклости наз-тсяточкой перегиба.
Т.(достаточный признак существования точки перегиба).
Если в точке 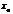
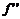
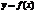 =0 и меняет знак при переходе через нее, то
=0 и меняет знак при переходе через нее, то 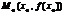 –точка перегиба.для х в 4 н выполняется.
–точка перегиба.для х в 4 н выполняется.
Асимптоты.
Если график ф-и сколь угодно близко приближается к прямой, то такую прямую наз-ют асимптотой.
О. Прямая 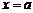 наз-тся вертикальной асимптотой графика ф-и
наз-тся вертикальной асимптотой графика ф-и 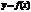 , если хотя бы одно из предельных значений
, если хотя бы одно из предельных значений 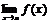 стремится к ¥.
стремится к ¥.
О.Предположим, что 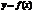 определена при сколь угодно больших по модулю значениях аргумента (будем рассм. «+» значения). Прямая
определена при сколь угодно больших по модулю значениях аргумента (будем рассм. «+» значения). Прямая 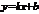 наз-тся наклонной асимптотой графика ф-и
наз-тся наклонной асимптотой графика ф-и 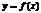 , если эта ф-я представлена в виде
, если эта ф-я представлена в виде 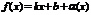 , где
, где 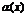 –бесконечно малая, то
–бесконечно малая, то 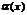 ®0, при
®0, при 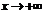 .
.
Т. (необходимое и достаточное условие существования наклонной асимптоты). График ф-и 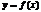 имеет при
имеет при 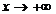 наклонную асимптоту
наклонную асимптоту 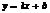 , если сущ-ют 2 конечных предела.
, если сущ-ют 2 конечных предела. 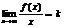 и
и 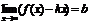
Исследование ф-и и построение графика:
I. Найти область определения (Д)
II. обл. значений
III. четность и периодичность
IV. точки пересечения с осями координат
V. изучить поведение ф-и при стремлении аргумента к концам обл. определения.
VI. точки экстремума и промежутки и ¯
VII. промежутки выпуклости ф-ий, точки перегиба
VIII. асимптоты графика
IX. построить график ф-и.
О. Ф-я 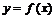 наз-тся четной, если: 1)
наз-тся четной, если: 1) 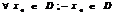 ; 2)
; 2) 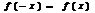
О. Ф-я 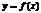 наз-тсяпериодической, если сущ-ет такое Т>0, что 1)
наз-тсяпериодической, если сущ-ет такое Т>0, что 1) 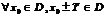
2) 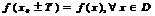
15)Скалярное, векторное и смешанное произведение векторов.
