IX. V2: Радиус сходимости степенного ряда

1. I:

S: Интервал сходимости степенного ряда 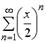имеет вид 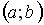. Тогда 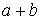равно …

+: 0

2. I:

S: Интервал сходимости степенного ряда 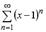имеет вид 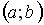. Тогда 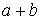равно …

+: 2

3. I:

S: Интервал сходимости степенного ряда 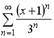имеет вид 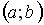. Тогда 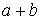равно …

+: -2

4. I:

S: Интервал сходимости степенного ряда 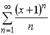имеет вид 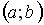. Тогда 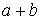равно …

+: -2

5. I:

S: Дан степенной ряд 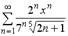. Количество целых чисел, принадлежащих его

интервалу сходимости равно …

+: 7

6. I:

S: Дан степенной ряд 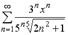. Количество целых чисел, принадлежащих его

интервалу сходимости равно …

+: 3

7. I:

S: Дан степенной ряд 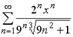. Количество целых чисел, принадлежащих его

интервалу сходимости равно …

+: 9

8. I:

S: Дан степенной ряд 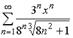. Количество целых чисел, принадлежащих его

интервалу сходимости равно …

+: 5

9. I:

S: Дан степенной ряд 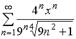. Количество целых чисел, принадлежащих его

интервалу сходимости равно …

+: 5

10. I:

S: Радиус сходимости степенного ряда 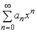равен 8, тогда интервал сходимости имеет вид…

+: (–8;8)

-: (–8;0)

-: (0;8)

-: (–4;4)

11. I:

S: Радиус сходимости степенного ряда 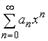равен 7, тогда интервал сходимости имеет вид…

+: (–7;7)

-: (0;7)

-: (–7;0)

-: (–3,5;3,5)

12. I:

S: Радиус сходимости степенного ряда 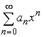равен 3, тогда интервал сходимости имеет вид…

-: (–1,5;1,5)

+: (–3;3)

-: (–3;0)

-: (0;3)

13. I:

S: Радиус сходимости степенного ряда 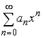равен 14, тогда интервал сходимости имеет вид…

+: (–14;14)

-: (0;14)

-: (–14;0)

-: (–7;7)

14. I:

S: Радиус сходимости степенного ряда 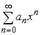равен 16, тогда интервал сходимости имеет вид…

-: (0;16)

+: (–16;16)

-: (–16;0)

-: (–8;8)

X. V2: Ряды Тейлора (Маклорена)

1. I:

S: Первый отличный от нуля коэффициент разложения функции 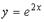в ряд Тейлора

по степеням х равен …

+: 1

2. I:

S: Первый отличный от нуля коэффициент разложения функции 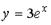в ряд Тейлора

по степеням х равен …

+: 3

3. I:

S: Первый отличный от нуля коэффициент разложения функции 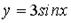в ряд Тейлора

по степеням х равен …

+: 3

4. I:

S: Первый отличный от нуля коэффициент разложения функции 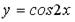в ряд Тейлора

по степеням х равен …

+: 1

5. I:

S: Первый отличный от нуля коэффициент разложения функции 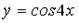в ряд Тейлора

по степеням х равен …

+: 1

6. I:

S: Если 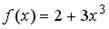, то коэффициент а₅ разложения данной функции в ряд Тейлора

по степеням (х-3) равен…

-: 3

+: 0

-: 10

-: 18

7. I:

S: Если 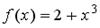, то коэффициент а₆ разложения данной функции в ряд Тейлора

по степеням (х+4) равен…

-: 6

-: 2

+: 0

-: 8

8. I:

S: Коэффициент 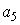в разложении функции 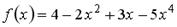в ряд Тейлора

по степеням (х-4) равен…

-: 4

-:

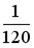
+: 0

-: 1

9. I:

S: Функция 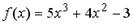разложена в ряд Тейлора по степеням (х-1).

Тогда коэффициент при 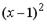равен …

-: 23

+: 19

-: 4

-: 38

10. I:

S: Функция 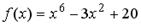разложена в ряд Тейлора по степеням (х-1).

Тогда коэффициент при 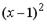равен …

-: 0

-: - 1

-: 24

+: 12

11. I:

S: Если 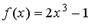, то коэффициент 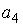разложения данной функции в ряд Тейлора

по степеням (х-1) равен…

-: 1

-: 0,25

+: 0

-: 2

12. I:

S: Если 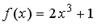, то коэффициент 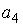разложения данной функции в ряд Тейлора

по степеням (х-1) равен…

-: 0,5

-: 1

-: 2

+: 0

13. I:

S: Если 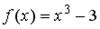, то коэффициент 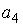разложения данной функции в ряд

по степеням (х+3) равен...

+: 0

-: 1

-: 3

-: 0,25

14. I:

S: Если 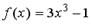, то коэффициент 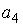разложения данной функции в ряд

по степеням (х+1) равен...

-: 0,75

-: 9

+: 0

-: 3

15. I:

S: Если 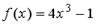, то коэффициент 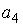разложения данной функции в ряд

по степеням (х-1) равен...

-: 4

-: 12

-: 1

+: 0

Тема. 3. V1: Численные методы