Глава XI. Функциональные ряды

11.1. Основные определения и примеры

Определение 11.1.

Ряд 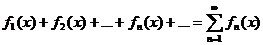, членами которого являются функции от x, определённые на множестве D, называется функциональным рядом.

Если числовой ряд 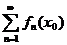сходится при 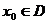, то x₀ называется точкойсходимости ряда.

Множество Х всех точек сходимости ряда 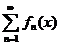называется областью сходимости ряда.

Определение 11.2.

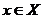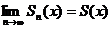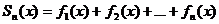Если для любого существует предел , где - частные суммы ряда, то говорят, что ряд сходится на множестве X к S(x). При этом функция S(x) называется суммой ряда .

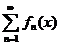Для нахождения области сходимости ряда 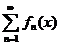можно использовать эталонные ряды и достаточные признаки сходимости числовых рядов.

Пример 11.1.

Найдём область сходимости ряда .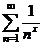

Данный ряд представляет собой обобщенный гармонический ряд, который сходится при x>1 и расходится при x≤1. Областью X сходимости ряда является интервал (1; + ∞).

Пример 11.2.

Найдем область сходимости ряда .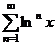

Данный ряд является геометрической прогрессией с q = lnx, которая сходится, если |q| = |lnx| < 1, откуда 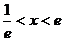. Область X сходимости ряда – интервал .

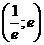Пример 11.3.

Найдем область сходимости ряда .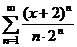

Для нахождения области сходимости данного ряда используем признак Даламбера, который применим лишь к рядам с положительными членами. Составим ряд из абсолютных величин членов данного ряда:

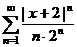и к нему применим признак Даламбера (теорема 10.6).

Имеем .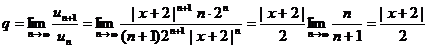

Ряд 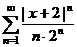будет сходиться, если 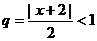, откуда -2<x+2<2 или

-4<x<0.

Тогда исходный ряд будет сходиться, и притом абсолютно в интервале

(-4,0).

При 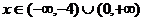этот ряд расходится, как не удовлетворяющий необходимому признаку сходимости (q>1) (следствие к теореме 10.2).

Если q=1, то ответа о сходимости ряда признак Даламбера не дает и при x=-4 и x=0 ряд нужно исследовать особо.

При x=-4 из исходного ряда получим числовой ряд =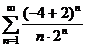

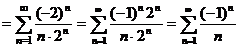, который сходится как ряд Лейбница (см. пример 10.15).

При х = 0 из ряда 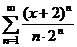получим 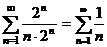, который является гармоническим рядом, а значит, расходится (см. пример 10.4.).

Итак, областью Х сходимости ряда 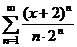будет промежуток [-4;0).

Степенные ряды. Свойства степенных рядов

Определение 11.3.

Степенным рядомназывается функциональный ряд вида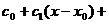

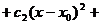
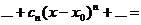
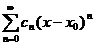, то есть ряд, членами которого являются степенные функции .

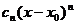Числа с_n /R называются коэффициентами степенного ряда, х₀ – центром степенного ряда.

Облостью Х сходимости степенного ряда является промежуток с центром в точке х₀. При этом промежуток может быть открытым, полуоткрытым или замкнутым, то есть иметь вид (х₀ – R_, х₀ + R), [х₀ – R, х₀+ R] соответственно (см. также пример 11.3). Число R называется радиусом сходимости степенного ряда.

Если степенной ряд сходится только в точке х₀, то считают, что R = 0, если же ряд сходится не всей числовой прямой, то считают, что R = +∞.

В примере 11.3 был рассмотрен степенной ряд 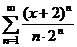с центром х₀ = -2. Областью Х сходимости ряда является полуоткрытый промежуток [-4; 0). Радиус сходимости данного степенного ряда равен 2.

Теорема 11.1.

Степенной ряд можно почленно дифференцировать в каждой точке x его промежутка сходимости сколько угодно раз, при этом радиус сходимости ряда не меняется.

Теорема 11.2.

Степенной ряд можно почленно интегрировать на любом отрезке, содержащемся в промежутке сходимости.

Пример 11.4.

Найдем сумму ряда .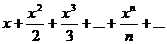

Обозначим сумму этого ряда через S(x), то есть

S(x)= .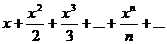

Легко показать, что промежуток сходимости этого ряда (-1;1). На основании теоремы 11.1 его можно почленно дифференцировать в каждой точке промежутка (-1;1): .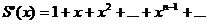

Справа в этом равенстве сумма геометрической прогрессии.

Если |q|=|x|<1, то 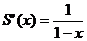, откуда 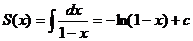. Зная, что S(0)=0, получим 0=-ln(1-0)+c, откуда c=0, S(x)=-ln(1-x).

Пример 11.5.

Найдем сумму ряда 1-3x²+5x⁴-…+(-1)^n-1(2n-1)x^2n-2+….

Обозначим сумму ряда через S(x),то есть

S(x)= 1-3x²+5x⁴-…+(-1)^n-1(2n-1)x^2n-2+….

Этот ряд сходится на промежутке (-1;1).

На основании теоремы 11.2 его можно почленно интегрировать на любом отрезке [0;x] 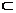(-1;1).

.

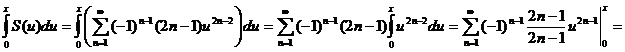
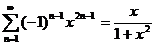Сумма последнего ряда есть сумма геометрической прогрессии, для которой q = -x².

Таким образом .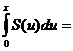

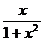Продифференцируем обе части этого равенства: 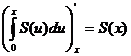, тогда имеем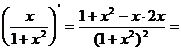 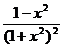, откуда

1-3x²+5x⁴-…+(-1)^n-1(2n-1)x^2n-2+…= 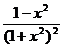.