Утверждено редакционно-издательским советом ВоГТУ
МАТЕМАТИКА
Методические указания
и контрольные задания для студентов заочной
формы обучения по сокращенным образовательным
программам
Специальность 220201 – управление и информатика в технических системах
Факультет электроэнергетический
Вологда
УДК 51:378.147 (075,5)
Математика: Методические указания и контрольные задания для студентов заочной формы обучения по сокращенным образовательным программам-Вологда: ВоГТУ, 2010.- 47 с.
Данные методические указания включают в себя две контрольные работы: по линейной алгебре и математическому анализу. Каждая работа состоит из четырех заданий по 30 вариантов каждое. Методические указания прелагаются для студентов-заочников специальности 220201 электроэнергетического факультета.
Утверждено редакционно-издательским советом ВоГТУ
Составитель: Абильдин А.А., канд.техн.наук, доцент
Рецензент: Быстроумов В.А., канд.техн.наук, доцент
ВВЕДЕНИЕ
Настоящие методические указания предназначены для самостоятельного изучения основ некоторых разделов курса «Высшая математика» студентами заочного обучения специальности 220201 «управление и информатика в технических системах» В них даны указания теоретические сведения , разобраны типовые примеры. Студент не должен ограничиваться рассмотрением только этих примеров, а может закрепить свои знания, решая примеры из соответствующих разделов сборников задач по линейной алгебре и математическому анализу. Указана литература, приведены задания для контрольных работ №1 и №2
.
ТЕМА 1. ВЕКТОРЫ. ЛИНЕЙНЫЕ ОПЕРАЦИИ НАД ВЕКТОРАМИ.
Вектором называется направленный отрезок 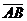 .Точка A называется началом вектора, точка B – концoм вектора.Векторы обозначают так же строчными буквами
.Точка A называется началом вектора, точка B – концoм вектора.Векторы обозначают так же строчными буквами 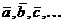 и пишут ā=
и пишут ā= 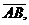
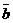 =
= 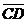
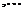 . Длину вектора
. Длину вектора 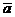 обозначаем через
обозначаем через 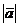 .Векторы
.Векторы 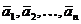 называются коллинеарными между собою,если все они,будучи приложенными в одной и той же точке, оказываются лежащими на одной прямой.
называются коллинеарными между собою,если все они,будучи приложенными в одной и той же точке, оказываются лежащими на одной прямой.
§1.1. Действия над векторами.
1.Сложение векторов.
Пусть даны векторы 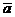 и
и 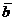 . Прилагаем вектор
. Прилагаем вектор 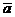 к какой-нибудь точке A,получаем
к какой-нибудь точке A,получаем 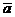 =
= 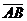 ; прилагаем
; прилагаем 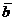 к точке B, получаем
к точке B, получаем 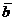 =
= 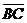 . По определению вектор
. По определению вектор 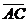 =
= 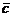 называется суммой векторов
называется суммой векторов 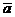 и
и 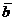 , т.е.
, т.е.
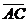 =
= 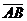 +
+ 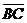

 B
B


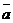
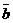
 A C
A C
рис.1
2.Умножение вектора на число.
Если отношение вектора CD к вектору AB равно числу 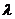 , то пишут
, то пишут 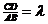 или CD=
или CD= 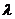 AB. Поэтому нахождение вектора CD, отношение которого к данному вектору AB равно данному числу
AB. Поэтому нахождение вектора CD, отношение которого к данному вектору AB равно данному числу 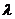 , называется умножением вектора на это число
, называется умножением вектора на это число 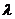 .
.
Замечание.
Линейной комбинацией векторов 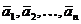 с коэффициентами
с коэффициентами 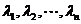 называется вектор вида
называется вектор вида 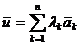 .
.
СКАЛЯРНОЕ ПРОИЗВЕДЕНИЕ
Определение.Скалярным произведением двух векторов 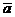 и
и 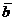 называется число (
называется число ( 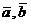 ), равное произведению длин этих векторов на косинус угла между ними
), равное произведению длин этих векторов на косинус угла между ними
( 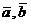 )=
)= 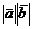 cos
cos 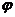 .
.
Следствие. Если два вектора 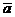 и
и 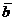 заданы своими декартовыми прямоугольными координатами,то скалярное произведение этих векторов равно сумме попарных произведений соответствующих координат, т.е.
заданы своими декартовыми прямоугольными координатами,то скалярное произведение этих векторов равно сумме попарных произведений соответствующих координат, т.е. 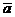 (
( 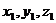 ),
), 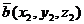
и 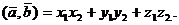
Свойства скалярного произведения.
a).( 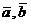 )=(
)=( 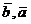 )
)
b).( 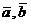 )=0 тогда и только тогда,когда векторы
)=0 тогда и только тогда,когда векторы 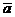 и
и 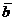 перпендикулярны между собою.
перпендикулярны между собою.
c).( 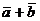 ,
, 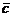 )=(
)=( 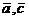 )+(
)+( 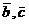 )
)
d).( 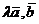 )=
)= 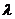 (
( 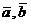 )-численный множитель можно выносить за знак скалярного произведения.
)-численный множитель можно выносить за знак скалярного произведения.
Транспонирование матриц
Транспонированием матриц называется такое преобразование исходной матрицы, когда столбцы преобразуются в строки и наоборот - строки в столбцы: 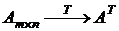
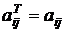 , где
, где 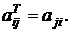
Пример
Транспонируя матрицу 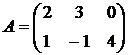 , получим
, получим 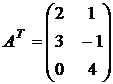 .
.
Сложение
Суммой двух матриц является третья матрица той же размерности, каждый элемент которой представляет сумму двух соответствующих элементов слагаемых матриц: 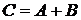 ;
; 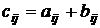 .
.
Пример. Складывая матрицы
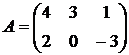 и
и 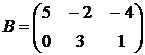 получим
получим 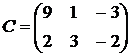 .
.
Умножение матрицы на скаляр
Произведением матрицы на скаляр l является матрица
 .
.
Каждый элемент матрицы А умножен на скаляр l.
Умножение матриц
Произведением матрицы Аmxn на матрицу Bnxr называется новая матрица Сmxr , каждый элемент которой представляет скалярное произведение соответствующей вектор-строки левой матрицы на вектор-столбец правого множителя:
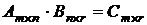 ,
,
где 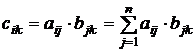 .
.
Пример
Рассмотрим произведение А2x4 × B4x3 = C2x3 или
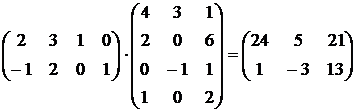 ,
,
где C11 = 14 представляет скалярное произведение вектор-строки ( 2; 3; 1; 0) на вектор-столбец ( 4; 2; 0; 1), т.е. 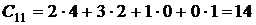 и т.д.
и т.д.
Правило. Перемножать можно матрицы только в том случае, когда количество столбцов первой (левой) матрицы равно количеству строк второй (правой) матрицы.
Cвойства операции умножения матрицы.
а) A(B+C)=AB+AC
b) (A+B)C=AC+BC
c) C(AB)=(CA)B
d) 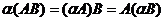 .
.
Определителем 2-го порядка называется число, получаемое из элементов матрицы 2-го порядка, представленных в виде квадратной таблицы. Он равен разнице произведений чисел, расположенных по главной и побочной диагоналям:
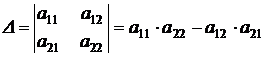 ,
,
где 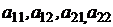 - элементы определителя;
- элементы определителя;
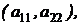 - главная диагональ;
- главная диагональ;
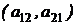 - побочная диагональ.
- побочная диагональ.
Определителем 3-го порядка называется число, которое можно найти по следующей формуле
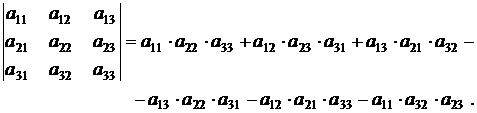
Определитель третьего порядка, также можно найти по теореме Лапласа:
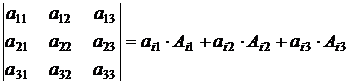
- это разложение по i-й строке. Чтобы вычислить алгебраическое дополнение Аi1 элемента аi1, вычеркнем мысленно из матрицы, например, вторую ( i = 2) строку и первый столбец, на пересечении которых стоит 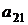 . Оставшемуся определителю второго порядка припишем знак (-1)2+1 :
. Оставшемуся определителю второго порядка припишем знак (-1)2+1 :
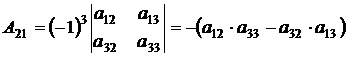
Следующий элемент во второй строке 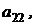 а алгебраическое дополнение элемента
а алгебраическое дополнение элемента 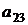 будет
будет 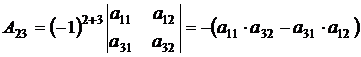 .
.
Обратная матрица
Пусть А - квадратная матрица. Матрица B называется обратной для матрицы А, если произведение этих матриц равно единичной матрице, т.е. АB = BA=E.
Если определитель квадратной матрицы не равен нулю, то эта матрица имеет обратную и притом единственную.
Правило.Для вычисления обратной матрицы необходимо осуществить следующие операции:
1. Вычислить определитель 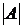 исходной матрицы; если он не равен нулю, то обратная матрица существует.
исходной матрицы; если он не равен нулю, то обратная матрица существует.
2. Вычислить алгебраические дополнения элементов исходной матрицы: А11, А12,..., Аn1,... Аnn .
3. Составить из алгебраических дополнений матрицу 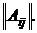
4. Транспонируя полученную матрицу, получить присоединенную 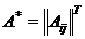 .
.
5. Разделив присоединенную матрицу на определитель, получить обратную матрицу 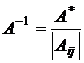 ,
,
6. Сделать проверку 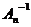 ∙
∙ 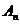 =E
=E 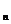
Пример. Вычислить обратную матрицу для 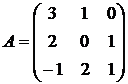 .
.
Проводим расчеты по пунктам, описанным выше:
1.
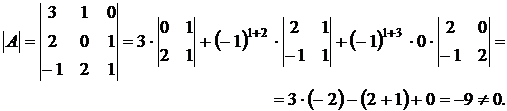
2.
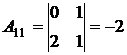 ,
, 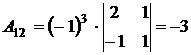 ,
, 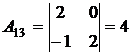 ,
,
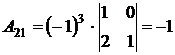 ,
, 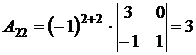 ,
, 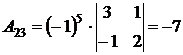 ,
,
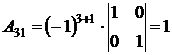 ,
, 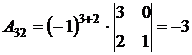 ,
, 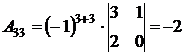 .
.
3.
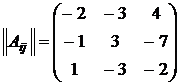 .
.
4.
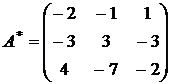 .
.
5.
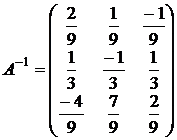 =-
=- 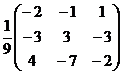
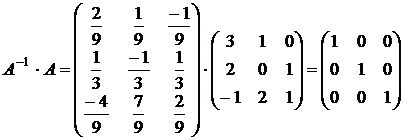 .
.
ТЕМА 4. ПРОИЗВЕДЕНИЕ ПРЕОБРАЗОВАНИЙ
Пусть даны линейные преобразования f и g соответственно с матрицами А и В в некотором базисе. Тогда произведение этих преобразований имеет матрицу ВА в том же базисе. Отметим, что в общем случае АВ ¹ ВА.
Например, преобразование g с матрицей 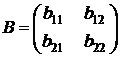 переводит точку М(х, у) в точку М¢(х¢, у¢) по формулам
переводит точку М(х, у) в точку М¢(х¢, у¢) по формулам
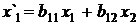
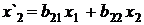 . (2)
. (2)
Преобразование А с матрицей 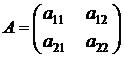 переводит точку М¢(х¢, у¢) в точку М²(Х2², У2²) по формулам
переводит точку М¢(х¢, у¢) в точку М²(Х2², У2²) по формулам
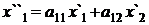 ,
, 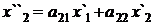 . (3)
. (3)
Чтобы получить формулы результирующего преобразования точки М в точку М², надо подставить в (3) выражения (2). Получим
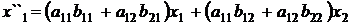 ,
,
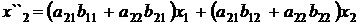 .
.
Стало быть, матрица произведения преобразований есть
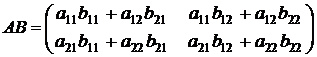 .
.
ТЕМА 5. СОБСТВЕННЫЕ ВЕКТОРЫ ЛИНЕЙНЫХ
ПРЕОБРАЗОВАНИЙ
Пусть j- линейное преобразование, 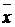 - вектор, отличный от нуля. Определение. Ненулевой вектор
- вектор, отличный от нуля. Определение. Ненулевой вектор 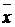 , удовлетворяющий равенству
, удовлетворяющий равенству
j 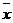 = l
= l 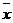 ,
,
где l -некоторое действительное число, называется собственным вектором преобразования j, число l - собственным значением этого преобразования.
Если А - матрица линейного преобразования, Х - матрица-столбец из координат вектора 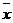 , то равенство (1) можно записать в матричном виде
, то равенство (1) можно записать в матричном виде
АХ = lХ.
Перенося члены в одну сторону получим
AX- 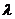 X=0 или (A-
X=0 или (A- 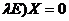
Уравнение 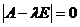 для собственных значений называется характеристическим
для собственных значений называется характеристическим
уравнением .
Пример
Пусть преобразование j имеет матрицу
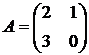 .
.
Найти собственные векторы матрицы.
Решение. Сначала найдем собственные значения матрицы. Характеристическое уравнение имеет вид
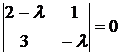 ,
,
или 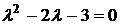 . Корнями этого уравнения являются l1 = -1,
. Корнями этого уравнения являются l1 = -1, 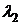 =3. Обозначаем через
=3. Обозначаем через 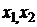 координаты собственного вектора
координаты собственного вектора 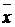 .
.
Тогда уравнение 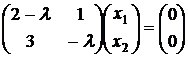 при l = l1 = -1 имеет вид
при l = l1 = -1 имеет вид
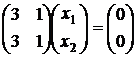 ,
,
или в раскрытом виде 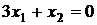 . Полагая
. Полагая 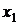 =a, найдем отсюда
=a, найдем отсюда 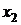 = -3a. Следовательно, собственные векторы, отвечающие корню l1, имеют вид
= -3a. Следовательно, собственные векторы, отвечающие корню l1, имеют вид 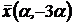 , где a - любое число, отличное от нуля.
, где a - любое число, отличное от нуля.
ТЕМА 6. КОМПЛЕКСНЫЕ ЧИСЛА
Комплексными называются числа вида z=x+iy, где x и y-действительные числа, а i2 =-1. Число x называется действительной частью комплексного числа z, а число y – коэффициент при i – мнимой частью. Число 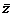 =x-iy называется сопряженным к числу z=x+iy. У сопряженных чисел равны действительные части, а мнимые отличаются только знаком. Числу z можно сопоставить вектор, направленный из начала O в точку z. Модуль
=x-iy называется сопряженным к числу z=x+iy. У сопряженных чисел равны действительные части, а мнимые отличаются только знаком. Числу z можно сопоставить вектор, направленный из начала O в точку z. Модуль 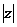 комплексного числа z вычисляется по формуле
комплексного числа z вычисляется по формуле
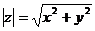 .
.
Угол 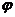 образованный радиусом-вектором Oz (рис.1) с положительным направлением действительной оси Оx, называется аргументом числа z и обозначается Argz.
образованный радиусом-вектором Oz (рис.1) с положительным направлением действительной оси Оx, называется аргументом числа z и обозначается Argz.
Любое комплексное число z можно представить в алгебраической форме z = x + iy и в тригонометрической форме z= r (cosj +isinj). Здесь 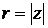 , j=Аrgz -, причем различные значения аргумента
, j=Аrgz -, причем различные значения аргумента 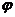 отличаются на 2
отличаются на 2 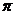 k
k  , где к - целое число. Под главным значением аргумента понимается значение j, удовлетворяющее условию -
, где к - целое число. Под главным значением аргумента понимается значение j, удовлетворяющее условию - 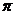 <j<
<j< 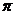 . Таким образом Аrgz = аrgz+2
. Таким образом Аrgz = аrgz+2 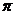 к.
к.
Комплексные числа z еще можно представить в показательной форме z =rеij, где r и j - то, что и в тригонометрической форме.
 y
y
z
 |
r
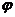
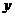
 o
o 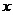 x
x
Рис.2
Пример
Найти корни уравнения 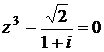 .
.
Решение. Находим модуль и аргумент числа 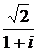
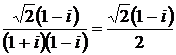
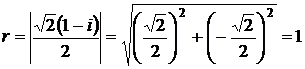
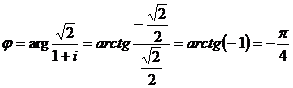 .
.
Тогда корни данного уравнения определяем по формулам
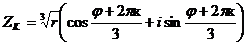 , к = 0,1,2, т.е. уравнение имеет три корня:
, к = 0,1,2, т.е. уравнение имеет три корня:
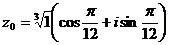 , при к=0;
, при к=0;
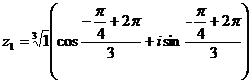 , при к=1;
, при к=1;
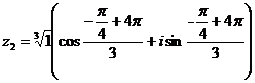 , при к=2
, при к=2
или 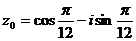
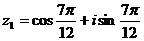
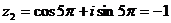
КОНТРОЛЬНАЯ РАБОТА № 1
Задание 1. Решить систему уравнений методом Гаусса и с помощью обратной матрицы
1. 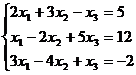
2. 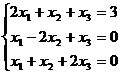
3. 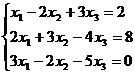
4. 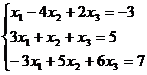
5. 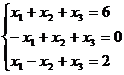
6. 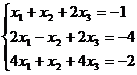
7. 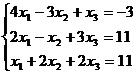
8. 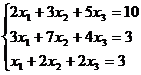
9. 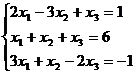
10. 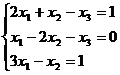
11. 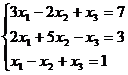
12. 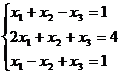
13. 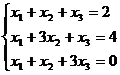
14. 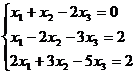
15. 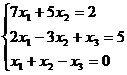
6. 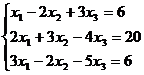
17. 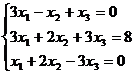
18. 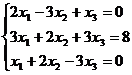
19. 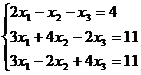
20. 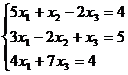
21. 
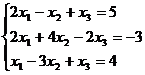
22. 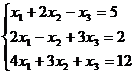
23. 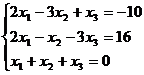
28. 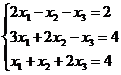
24. 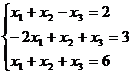
25. 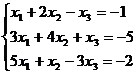
26. 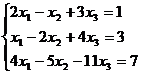
27. 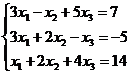

 29.
29. 
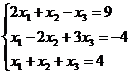
30. 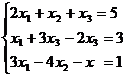

Задание 2.
В задачах 1-30 даны два линейных преобразования. Средствами матричного исчисления найти преобразование, выражающее X"= 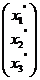 через X=
через X= 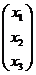
1. 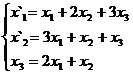
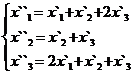
2. 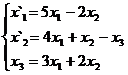
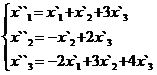
3. 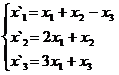
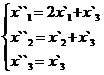
4. 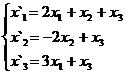
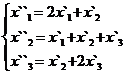
5. 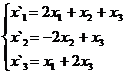
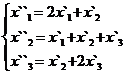
6. 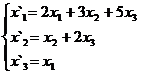
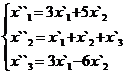
7. 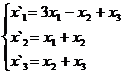
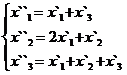
8. 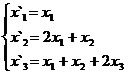
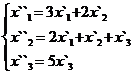
9. 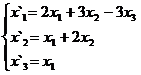
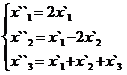
10. 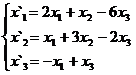
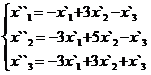
11. 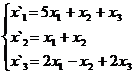
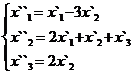
12. 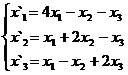
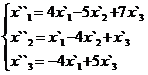
13. 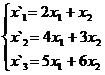
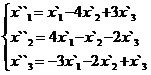
14. 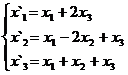
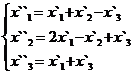
15. 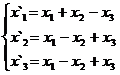
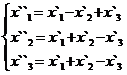
16. 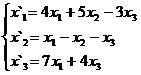
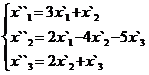
17. 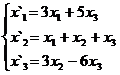
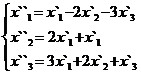
18. 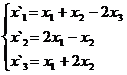
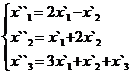
19. 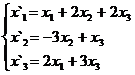
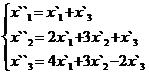
20. 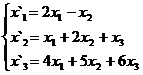
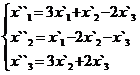
21. 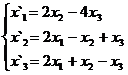
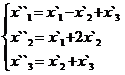
22. 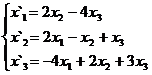
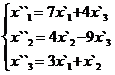
23. 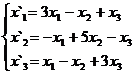
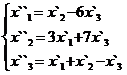
24. 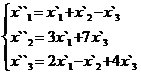
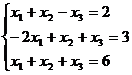
25. 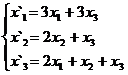
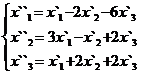
26. 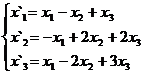
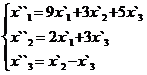
27. 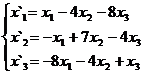
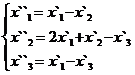
28. 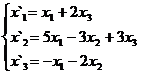
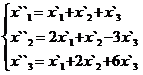
29. 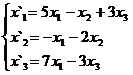
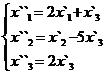
30. 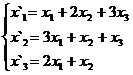
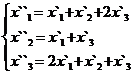
Задание 3.
Найти собственные векторы и собственные значения линейного преобразования, заданного в некотором базисе матрицей.
1. 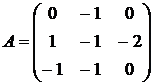 2.
2. 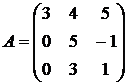 3.
3. 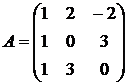
4. 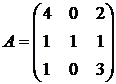 5.
5. 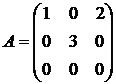 6.
6. 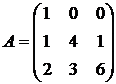
7. 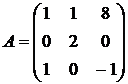 8.
8. 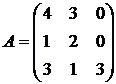 9.
9. 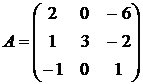
10.  11.
11. 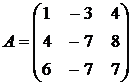 12.
12. 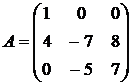
13. 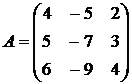 14.
14. 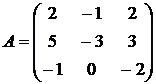 15.
15. 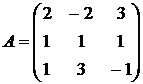
16. 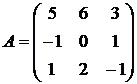 17.
17.  A=
A= 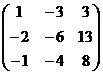 18.
18. 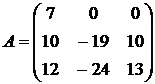
19. 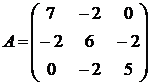 20.
20. 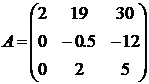 21.
21. 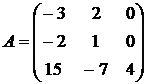
22. 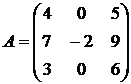 23.
23. 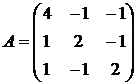 24.
24. 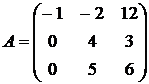
25. 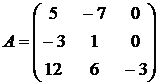 26.
26. 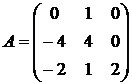 27.
27. 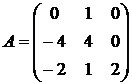
28. 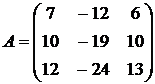 29.
29. 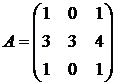 30.
30. 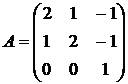
Задание 4.
Дано комплексное число 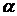 :
:
1) Записать число 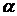 в алгебраической и тригонометрической формах.
в алгебраической и тригонометрической формах.
2) Найти и изобразить на плоскости все корни уравнения Z3 + 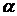 = 0.
= 0.
1. 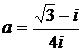 2.
2. 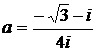 3.
3. 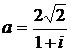 4.
4. 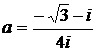
5. 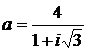 6.
6. 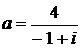 7.
7. 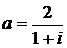 8.
8. 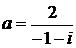
9. 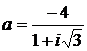 10.
10. 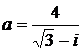 11.
11. 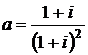 12.
12. 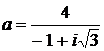
13. 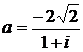 14.
14. 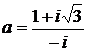 15.
15. 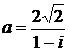 16.
16. 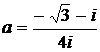
17. 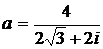 18.
18. 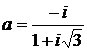 19.
19. 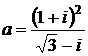 20.
20. 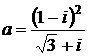
21. 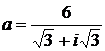 22.
22. 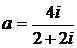 23.
23. 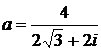 24.
24. 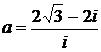
25. 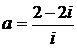 26.
26. 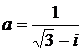 27.
27. 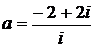 28.
28. 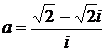
29. 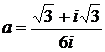 30.
30. 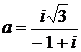
Пример 2.
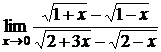
Подстановка предельного значения x ( т.е. числа 0) приводит к неопределенности вида 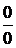 . Преобразуем дробь под знаком предела до того как
. Преобразуем дробь под знаком предела до того как 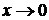 .
.

| |
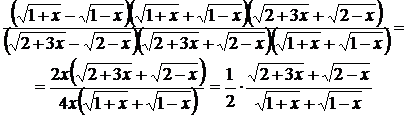
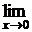
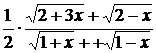 =
= 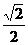 .
.
Пример 3.
Найти 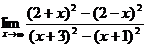 .
.
Здесь выражение под знаком пределов представляет собой отношение двух многочленов аргумента n. И числитель и знаменатель дроби стремятся к бесконечности. В этом случае говорят, что имеется «неопределенность типа 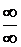 ».
».
Для отыскания предела следует раскрыть скобки и разделить числитель и знаменатель на высшую степень.
Получаем
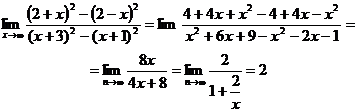
Так как 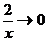 при
при 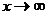 .
.
Пример 4.
Найти 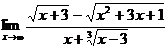 .
.
Как и в примере 3 целесообразно числитель и знаменатель дроби разделить на старшую степень, которую легко увидеть, если под каждым корнем оставить лишь старшую степень n (остальные слагаемые играют малую роль при 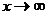 ).
).
В данном примере получаем 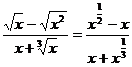 .
.
Значит старшая степень -x. Разделив числитель и знаменатель на x, будем иметь 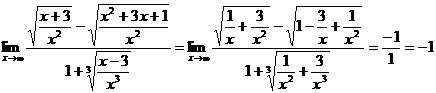 , так как
, так как 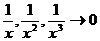 при x
при x 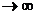
Пример 5.
Найти 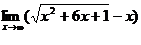 .
.
Здесь мы имеем «неопределенность типа ( 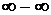 )».
)».
Умножив и разделив эту разность на сопряженное выражение 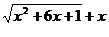 , получим
, получим 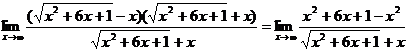
.
Такой предел рассматривался в предыдущем примере. Разделив числитель и знаменатель на x, будем иметь 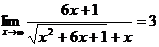 .
.

Пример 6.
Вычислить 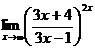
Здесь основание степени 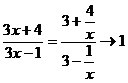 при x
при x 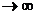 ,а показатель
,а показатель 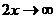 ; таким образом имеем «неопределенность типа
; таким образом имеем «неопределенность типа 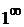 ». В этом случае следует воспользоваться вторым замечательным пределом:
». В этом случае следует воспользоваться вторым замечательным пределом: 

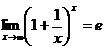 .
.
Преобразовав выражение, получаем
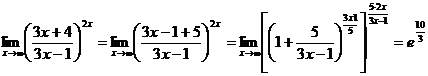 ,
,
так как выражение в квадратных скобках стремится к е, а 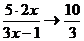 при
при 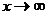 .
.
Пусть, например, требуется вычислить 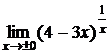 .
.
Рассмотрим случай 
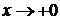 , тогда показатель стремится к
, тогда показатель стремится к 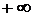 , основание к 4, значит искомый предел равен
, основание к 4, значит искомый предел равен 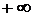 . Если
. Если 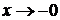 , то показатель
, то показатель 
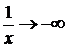 ,основание стремится к 4 и искомый предел равен 0. Итак
,основание стремится к 4 и искомый предел равен 0. Итак
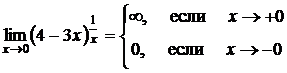 .
. 
Пример 7.
Найти 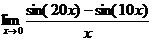 .
.
Для решения применим предел 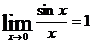
Здесь при 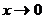 и числитель и знаменатель стремятся к нулю, получаем «неопределенность типа
и числитель и знаменатель стремятся к нулю, получаем «неопределенность типа 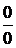 ». Используя формулу тригонометрии
». Используя формулу тригонометрии
имеем
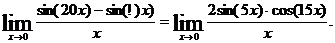
Заметим, что cos(15x) 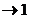 при x
при x 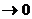 , поэтому
, поэтому
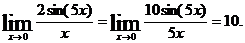
Пример 8.
Найти 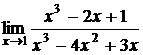 .
.
Известно ( следствие теоремы Безу), что если многочлен обращается в нуль при 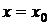 , то он делится без остатка на
, то он делится без остатка на 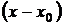 , поскольку и числитель и знаменатель рассматриваемой дроби обращается в нуль при х=1 «неопределенность типа
, поскольку и числитель и знаменатель рассматриваемой дроби обращается в нуль при х=1 «неопределенность типа 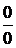 », то как и в предыдущей задаче, можно сократить дробь на х-1. Разделив числитель и знаменатель на x-1
», то как и в предыдущей задаче, можно сократить дробь на х-1. Разделив числитель и знаменатель на x-1
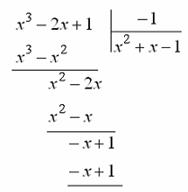
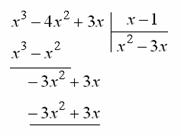
получаем
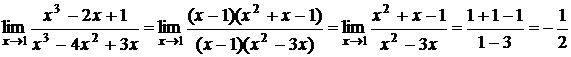 .
.
Пример 9.
Найти точки разрыва функции 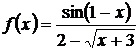 . Изобразить график в окрестности точки разрыва.
. Изобразить график в окрестности точки разрыва.
Знаменатель 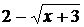 , при х=1 обращается в нуль и значит f(x) при x=1 не существует, следовательно, x=1 - точка разрыва функции. Для определения типа разрыва надо найти пределы функции слева и справа при х=1.
, при х=1 обращается в нуль и значит f(x) при x=1 не существует, следовательно, x=1 - точка разрыва функции. Для определения типа разрыва надо найти пределы функции слева и справа при х=1.
