Миноры и алгебраич. дополнения. Разложение определит. по элементам

1) рассмотрим кв. матрицу А размером NxN

из общего числа n2 элементов этой матрицы мы можем сделать выборки, содержащие n элементов, т.об. что бы в нее входило по одному элементу из каждой строки и каждого столбца (а1j1, a2j2,…, anjn)

упорядочены по номерам строк.

определит. кв. матрицы NxN наз. сумма произвед. таких выборок взятых с определенным знаком.

n!

|А|= ∑(а1j1* a2j2*…* anjn)(-1)R(J)

NxN (J)

всего в этой сумме n! слогаемых.

n! – наз. произвед. всех чисел от 1 до n, при этом n! =1.

n!=n*(n-1)!

знак слагаемых зависит от конкретной выборки.

2)минором Мij элемента aij, матрицы n-го порядка наз. определит. матрицы (n-1)-го порядка, полученной из матрицы А вычеркиванием i-й строки и j-го столбца.

Ex: минором элемента a12 матрицы А третьего порядка будет:

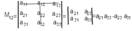
каждая матрица n-го порядка имеет n2 миноров (n-1)-го порядка.

3) Алгебраич. дополнением Aij элемента aij матрицы n-го порядка наз. его минор, взяты со знаком (-1)i+J

Aij = (-1)i+j Mij

т.е алгебраич. дополнение совпадает с минором, когда сумма номеров строки и столбца (i+j) –четное число, отличается от минора знаком, когда (i+j) – нечетное число.

4)Важное значение для вычесления определителя имеет теорема Лапласа .

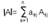т. Лапласа: определит. кв. матрицы равен сумме произведен. элементов любой строки (столбца) на их алгебраич. дополнения.

- столбца

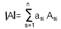
-разложение по элементам

i-той строки

разложим по элементам первой строки.

а11А11+а12А12+а13А13

теорема Лапласа позволяет свести вычисление опред. n-го порядка к вычислению более простых определит. (n-1)-го порядка

4.Св-ва определит.

1. если какая либо строка (столбец) матрицы состоит из 0-ей, то ее определит. равен 0.

2. Если все элементы какой либо строки (столбца) матрицы умножить на число λ, то ее определитель умножиться на это число λ.(пусть определит. исходной матрицы равен Δ. Эля определенности первую строку матрицы умножим на λ, получим новый определитель Δ΄, который разложим по элементам первой строки: Δ= (матрица) = λа11А11+ λа12А12+…+ λа1nА1n = λ(а11А11+ а12А12+…+ а1nА1n) = λΔ

3. При транспонировании матрицы ее определитель не изменяется: |А΄| = |А|

4. при перестановке двух строк (столбцов) матрицы ее определитель меняет знак на противоположный.

5. Если квадратная матрица содержит 2 одинаковые строки (столбца), то ее определитель равен 0.

6. Если элементы двух строк (столбцов) матрицы пропорциональны, то ее определитель равен 0.

7. Если к элементам какой либо строки (столбца) прибавить элементы другой строки (столбца) умножить на одно и то же число, то определит. матрицы не измениться.

n

∑ aij Akj= 0 i≠k

J=1

сумма элементов какой-либо строки (столбца) на алгебраич. дополнения другой строки (столбца) равна 0.

8. определитель произведения 2-х кв. матриц равен произведению их определителей: |С|=|А|*|В|, где С = А*В; А и В – матрицы n-го порядка.

Св-ва позволяют упростить процесс вычисления высокого порядка.