Понятия функционального ряда. Свойства равномерно сходящихся рядов.

Как мы уже отмечали, членами бесконечного ряда могут быть не только числа, но и функции, например,

Суммой такого ряда также является функция, значение которой в каждой точке получается как предел вычисленных в этой точке частичных сумм.

Ряд может сходиться в среднем квадратичном, даже если он не сходится ни в одной отдельной точке. Существуют также и другие определения сходимости функционального ряда.

Некоторые функциональные ряды получили название по тем функциям, которые в них входят. В качестве примера можно привести степенные ряды и их суммы:

РАВНОМЕРНО СХОДЯЩИЙСЯ РЯД

функциональный ряд 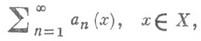(1)

Условие равномерной сходимости ряда (1) на множестве Xбез использования понятия суммы ряда дает Ноши критерий равномерной сходимости ряда. Достаточное условие равномерной сходимости ряда дается Вейерштрасса признаком.

т. е. если ряд (1) удовлетворяет условиям признака Веяорштрасса равномерной сходимости рядов. В силу этого признака правильно сходящийся на множестве Xряд равномерно сходится на этом множестве. Обратное, вообще говоря, неверно; однако во всяком равномерно сходящемся на множестве Xряде можно так объединить следующие друг за другом его члены в конечные группы, что получившийся при этом ряд будет уже правильно сходиться на множестве X.

Степенные ряды. Теорема Абеля. Св-ва степенных рядов. Радиус Сходимости степенного ряда.

Степенные ряды- ряды, членами которых являются степенные функции.

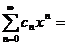C₀+C₁X+С₂Х²+...+С_nХⁿ (С_n-коэф степенного ряда).

Область сходимости степенного ряда-множество значений х, на котором ряд сходится.

Т.Абеля.

1)Если степенной ряд сходится при значении х= 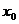≠0, то он сходится при том абсолютно, при всех значениях х таких, что |х|<|х₀|

2) Если степенной ряд расходится при х=x_1, то он расходится при всех значениях х таких, что |x|>|x₁|.

Из теор следует, что сущ-ет такое число R≥0, что при |x|<R ряд сходится, а при |x|>R- расходится. R-радиус сходимости. (-R;R)-интервал схо-ти. На концах интервала сходимости ряд может и сходиться, и расходиться.

R=1/lim(n→∞)ⁿ√|C_n| (коши); R=lim(n→∞)||C_n\C_n+1|.

Свойства степенных рядов. На любом отрезке [a,b] целиком принадлежащем интервалу сходимости (-R;R), ф-ция f(x) яв-ся непрерывной, а => степенной ряд можно почленно интегрировать на этом отрезке:

Можно дифференцировать:

f’(x)=С₁+2С₂X+3С₃X²+..+nC_nX^n-1

После этих операций R не меняется.

Ряды Тейлора и Маклорена.

Ряд Маклорена:

Пусть f(x)- определенная и n-раз дифференцированная в окрестности точки х=0 функция, она может быть представлена ввиде степенного ряда( разложена в степенной ряд).

f(x)= 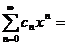C₀+C₁X+С₂Х²+...+С_nХⁿ

коэф-ты ряда:

f’(x)=C₁+2C₂X+3C₃X²+...+nC_nX^n-1

f“(x)=2C₂X+3∙2C₃X+...+n(n-1)C_nX^n-2

х=0,

f’(0)= C₁ => С₀=f(0)

f”(0)=2∙1 C₂=>C₁=f’(0)

f’”(0)=3∙2C₃ =>C₂=f”(0)/2!

f⁽ⁿ⁾(0)=n!C_n =>C_n=f⁽ⁿ⁾(0)/n!

Ряд Макларена: f(x)=f(0)+f’(0)∙x\1!+ f”(0)∙x²\2!+ f”’(0)∙x³\3!+..+ fⁿ(0)∙xⁿ\n!+..

Замечание1. Не всякая ф-ция может быть разложена в ряд Мак-на. Может получиться расх-ся ряд или ряд будет сводиться к др ряду.

Замечание2. Достаточное условие разложения ф-ции вряд Мак-на яв-ся ограниченность всех её производных в окрестности т.Х=0 одним и тем же числом, т.е. |f⁽ⁿ⁾(x)|≤C

*Если ф-ция раскладывается в ряд Маклорена, то это разложение единств-е.

Пр1: y=e^x

F(x)=1+x\1!+x²\2!+x³\3!+..+ xⁿ\n!+.. Отв:(-∞;+∞)

Пр2: f(x)=sinx

f’(x)=cosx, f’(0)=1

cos’x=-sinx, f”(0)=0

(-sinx)’=-cosx, f”’(0)=-1

(-cosx)’=sinx, f^IV(0)=0

Ряд: sinx=x- x³\3!+ x⁵\5!- x⁷\7!+..+(-1)ⁿx²ⁿ⁺¹\(2n+1)!+..

Ряд Тейлора:

Если ф-ция f(x) (n-1) раз дифференцируемых в окрестности т.Х₀, то для любого значения х из этой окрестности справедливы ф-ции Тейлора:

f(x)=f(x₀)+f’(x₀)(x-x₀)+f”(x₀)(x-x₀)²\2!+..+ fⁿ(x₀)(x-x₀)ⁿ\n!+Rn(x); Rn-остаточный член формулы Тейлора.

Rn= f⁽ⁿ⁺¹⁾(ξ)(x-x₀)ⁿ⁺¹\(n+1)!