Функции, непрерывные на отрезке, и их свойства. Теорема об устойчивости знака непрерывной функции, теоремы Больцано-Коши о промежуточном значении.
Функция  называется непрерывной на интервале
называется непрерывной на интервале 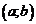 , если она непрерывна в каждой точке
, если она непрерывна в каждой точке 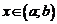 . Если же, кроме того, функция
. Если же, кроме того, функция  непрерывна в точке а справа, а в точке
непрерывна в точке а справа, а в точке 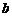 – слева, то функция
– слева, то функция  называется непрерывной на отрезке
называется непрерывной на отрезке  .
.
Функция  называется кусочно-непрерывной на отрезке
называется кусочно-непрерывной на отрезке  , если она непрерывна во всех внутренних точках
, если она непрерывна во всех внутренних точках  , за исключением конечного числа точек, в которых она имеет разрывы первого рода, а в точках а и
, за исключением конечного числа точек, в которых она имеет разрывы первого рода, а в точках а и 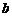 имеет соответствующие односторонние пределы.
имеет соответствующие односторонние пределы.
Монотонность и непрерывность.Будем считать, что функция  задана на отрезке
задана на отрезке  .
.
Утверждение 1. Монотонная на отрезке  функция
функция  может иметь точки разрыва только первого рода.
может иметь точки разрыва только первого рода.
Согласно этому утверждению, множество значений монотонной функции будет отрезком в том и только в том случае, если  – непрерывная функция на отрезке
– непрерывная функция на отрезке  .
.
Утверждение 2 (об устойчивости знака непрерывной функции). Пусть функция  непрерывна в точке
непрерывна в точке 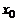 и
и  . Тогда существует
. Тогда существует 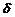 -окрестность точки
-окрестность точки 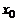 , такая, что в этой окрестности функция
, такая, что в этой окрестности функция  имеет тот же знак, что и
имеет тот же знак, что и 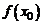 .
.
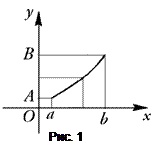
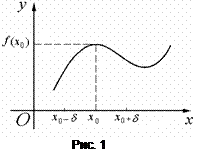 Геометрический смысл этого утверждения состоит в том, что, если функция
Геометрический смысл этого утверждения состоит в том, что, если функция  непрерывна в точке
непрерывна в точке 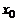 и отлична в ней от нуля, то некоторая часть графика этой функции, проходящая через точку
и отлична в ней от нуля, то некоторая часть графика этой функции, проходящая через точку 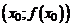 , не пересекает ось
, не пересекает ось 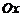 (рис. 1).
(рис. 1).
Теорема 1 (первая теорема Больцано-Коши).Пусть функция  непрерывна на отрезке
непрерывна на отрезке  и на концах отрезка имеет значения разных знаков. Тогда существует точка
и на концах отрезка имеет значения разных знаков. Тогда существует точка 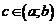 , в которой
, в которой 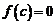 .
.
 Геометрический смысл этой теоремы также очевиден. Поскольку функция
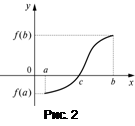
Геометрический смысл этой теоремы также очевиден. Поскольку функция 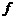 непрерывна на отрезке, то ее график состоит из одного «сплошного» куска. Эта кривая соединяет точки
непрерывна на отрезке, то ее график состоит из одного «сплошного» куска. Эта кривая соединяет точки 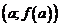 ,
, 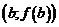 , одна из которых лежит ниже оси Ox, вторая – выше оси Ox. Следовательно, существует точка с на оси Ox, в которой график пересекает ось Ox (рис. 2).
, одна из которых лежит ниже оси Ox, вторая – выше оси Ox. Следовательно, существует точка с на оси Ox, в которой график пересекает ось Ox (рис. 2).
Теорема 2 (вторая теорема Больцано-Коши).Пусть функция  непрерывна на отрезке
непрерывна на отрезке 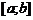 , причем
, причем 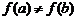 . Тогда, если С – любое число, лежащее строго между
. Тогда, если С – любое число, лежащее строго между 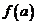 и
и 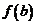 , то существует точка
, то существует точка 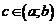 , такая, что
, такая, что 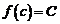 .
.
Другими словами, непрерывная на отрезке  функция принимает любое свое промежуточное значение.
функция принимает любое свое промежуточное значение.
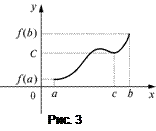 Геометрический смысл этой теоремы показан на рис. 3.
Геометрический смысл этой теоремы показан на рис. 3.
Теорема 3 (первая теорема Вейерштрасса).Если функция  непрерывна на отрезке
непрерывна на отрезке  , то она ограничена.
, то она ограничена.
Таким образом, если функция  непрерывна на отрезке
непрерывна на отрезке  , то существует число
, то существует число 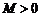 такое, что
такое, что 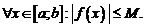
Заметим, что если в теореме 3 вместо отрезка  рассматривать интервал
рассматривать интервал 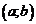 или какой-либо полуинтервал, то функция
или какой-либо полуинтервал, то функция  может быть и неограниченной, т. е. в этом случае утверждение об ограниченности несправедливо. Например, функция
может быть и неограниченной, т. е. в этом случае утверждение об ограниченности несправедливо. Например, функция 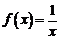 непрерывна на полуинтервале
непрерывна на полуинтервале 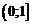 , но не ограничена на нем.
, но не ограничена на нем.
Теорема 4 (вторая теорема Вейерштрасса).Непрерывная на отрезке  функция
функция  достигает в некоторых точках отрезка
достигает в некоторых точках отрезка  своих точных верхней и нижней границ, т.е. существуют точки
своих точных верхней и нижней границ, т.е. существуют точки 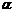 и
и 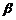 , принадлежащие
, принадлежащие  , для которых имеет место
, для которых имеет место
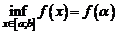 ,
, 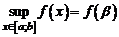 .
.
Таким образом, 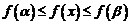 для всех
для всех 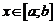 .
.
Поскольку непрерывная на отрезке  функция
функция 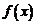 достигает в некоторых точках своих точных верхней и нижней границ, то можно называть точную верхнюю границу максимальным значением функции, а точную нижнюю границу – ее минимальным значением на отрезке
достигает в некоторых точках своих точных верхней и нижней границ, то можно называть точную верхнюю границу максимальным значением функции, а точную нижнюю границу – ее минимальным значением на отрезке  .
.
41. Обратная функция и её непрерывность.
Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией.
Имеет место следующая
Теорема 1. Если функция 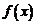 непрерывна и монотонна на отрезке
непрерывна и монотонна на отрезке  , то на множестве ее значений
, то на множестве ее значений 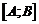 существует монотонная, непрерывная обратная функция.
существует монотонная, непрерывная обратная функция.
 Функции
Функции 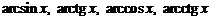 , обратные функциям
, обратные функциям 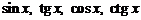 , в силу названного свойства непрерывны при всех значениях
, в силу названного свойства непрерывны при всех значениях 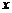 , при которых эти функции определены.
, при которых эти функции определены.
Пример 1.Функция 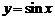 непрерывна и монотонна на отрезке
непрерывна и монотонна на отрезке 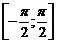 . Образом этого отрезка, посредством функции
. Образом этого отрезка, посредством функции 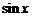 , является отрезок
, является отрезок 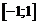 . На основании приведенного свойства существует определенная на отрезке
. На основании приведенного свойства существует определенная на отрезке 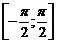 , обратная к функции
, обратная к функции 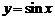 , непрерывная возрастающая функция
, непрерывная возрастающая функция 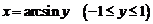 .
.
Для функции 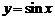 , рассматриваемой на всей действительной оси, не существует обратной функции, так как
, рассматриваемой на всей действительной оси, не существует обратной функции, так как 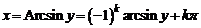 ,
, 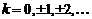 , т.е. каждому
, т.е. каждому 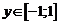 соответствует множество значений
соответствует множество значений 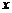 , определяемых указанной формулой. □
, определяемых указанной формулой. □
