Нахождение наибольшего,меньшего знач ФПН

Свойство. Если функция f(x, y, …) определена и непрерывна в замкнутой и

ограниченной области D, то в этой области найдется по крайней мере одна точка

N(x₀, y₀, …), такая, что для остальных точек верно неравенство

f(x₀, y₀, …) ³f(x, y, …)

а также точка N₁(x₀₁, y₀₁, …), такая, что для всех остальных точек верно неравенство

f(x₀₁, y₀₁, …) £f(x, y, …)

тогда f(x₀, y₀, …) = M – наибольшее значение функции, а f(x₀₁, y₀₁, …) = m – наименьшее значениефункции f(x, y, …) в области D.

Непрерывная функция в замкнутой и ограниченной области D достигает по крайней мере один раз наибольшего значения и один раз наименьшего.

38. Условный экстремум находится, когда переменные х и у, входящие в функцию u = f( x, y), не являются независимыми, т.е. существует некоторое соотношение j(х, у) = 0, которое называется уравнением связи.

Тогда из переменных х и у только одна будет независимой, т.к. другая может быть выражена через нее из уравнения связи.

Тогда u = f(x, y(x)).

В точках экстремума:

=0 (1)

Кроме того: (2)

Умножим равенство (2) на число l и сложим с равенством (1).

Для выполнения этого условия во всех точках найдем неопределенный коэффициент l так, чтобы выполнялась система трех уравнений:

Полученная система уравнений является необходимыми условиями условного экстремума. Однако это условие не является достаточным. Поэтому при нахождении критических точек требуется их дополнительное исследование на экстремум.

39.нахождение интегралов вида Интеграл вида 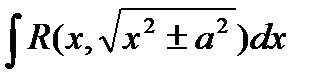подстановкой или сводится к интегралу от рациональной функции относительно sint или cost.

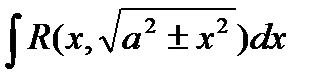находиться с помощью подстановк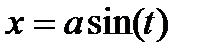и или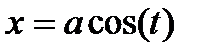

41. Полные дифференциалы высших порядков от ФНП. Пусть функция f(x)- дифференцируема на некотором интервале. Тогда, дифференцируя ее, получаем первую производную

Если найти производную функции f¢(x), получим вторую производнуюфункции f(x).

т.е. y¢¢ = (y¢)¢ или .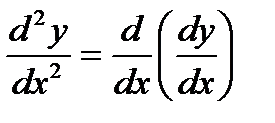

Этот процесс можно продолжить и далее, находя производные степени n.

.

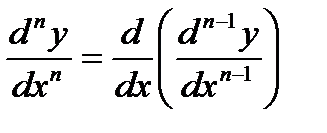42.Уравнения с разделяющимися переменными.Дифференциальное уравнение первого порядка в общем виде записывается так: F(x,y,y') = 0.(24.6) Если это уравнение разрешимо относительно у', то y'=f(x,y) (24.7) или dy-f(x,y)dx = 0. (24.8) Последнее уравнение является частным случаем уравнения. P(x,y)dx+Q(x,y)dy=0 (24.9).Задача Коши для дифференциального уравнения первого поряд­ка: найти решение у = у(х) уравнения (24.6), удовлетворяющее усло­вию у = уо при х = хo, или у(хo) = уо, (24.10)где хo, уо - заданные числа. Геометрически задача Коши означает сле­дующее: найти L интегральную линию, проходящую через точку Мo(хo, уо).Если в уравнении у' = f(x, у) функция f(x, у) и ее частная производная по у, непрерывны в некоторой области G плоскости Оху, содержащей точку Mo(xo, уо), то решение задачи Коши существует и являет­ся единственным. В этом случае через точку Mo(xo, уо) проходит един­ственная интегральная линия. Рассмотрим частный случай, а именно, ко­гда функции Р(х, у) и Q(x, у) представляют собой произведения функ­ции только от х на функцию только от у, т.е. Р(х, у) =f(x)j (у), Q(x, у) =fi(x)j1(y), в этом случае уравнение принимает вид f(x)j(y)dx+f1(x)jl(y)dy = 0. (24.11)Дифференциальное уравнение первого порядка называется уравнением с разделяющимися переменными, если его можно привести к виду (24.11), где f(x), f1(x) - функции только от х,j(у), ,j1(у) - функ­ции только от у.Разделив почленно это уравнение на f1(х)j(у) в предположении, что , f1(х)j(у)=0 (24.12) получим уравнение 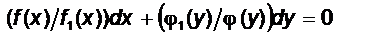(24.13) Уравнение (24.13) называется уравнением с разделенными пере­менными.

43.Линейные дифференциальные уравнения первого порядка.Линейным дифференциальным уравнением первого порядка на­зывается уравнение вида а(х)y' + b(х)у = с(х), (24.22) где у = у(х) - искомая функция; а(х), b(х), с(х) - заданные функции. Будем считать, что они непрерывны на отрезке [a, b], причем а(х) не равно 0. Поскольку а(х) не равно 0 при любом хÎ[а, b], то данное уравнение можно переписать так: y'+p(x)y=f(x). (24.23)Решение уравнения будем искать в виде произведения двух функций v = v(x), u = u(х) - y = uv. (24,24) Так как у' = u'v + uv', то подстановка выражений для у и у' в уравнение (24.23) приводит его к виду u'v + uv' + p(x)uv =f(x), или u'v + u[v'+p(x)v]=f(x). (24.25) В качестве v выберем одну из функций, обращающих в нуль сумму в квадратных скобках, т.е. функцию, удовлетворяющую уравне­нию v'+p(x)v = 0. (24.26) С учетом (24.26) уравнение (24.25) принимает вид u'v =f(x).(24.27)

Уравнение (24.26) является уравнением с разделяющимися пе­ременными х и v, из него определяется функция v = v(x). Функция u = u(х) определяется из уравнения (24.27), которое при v = v(x) также является уравнением с разделяющимися переменными. Определив u = u(х) и v = v(x), по формуле (24.24) найдем у. 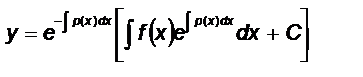(24.30)

44.Однородные дифференциальные уравнения первого порядка.Функция F(x, у) называется однородной измерения n, если при любом t выполняется тождество F(tx,ty)=tⁿF(x,y). (24.15) Дифференциальное уравнение первого порядка P(x,y)dx + Q(x,y)dy = 0 (24.16)называется однородным, если Р(х, у) и Q(x, у) - однородные функции одного и того же измерения n. В этом случае соотношение (24.15) принимает вид P(tx,ty)= tⁿP(x,y), Q(tx,ty)= tⁿQ(x,y).

Полагая в последних равенствах t = 1 :х, х не равно 0, получаем P(1,y/x)dx+Q(1,y/x)dy=0 (24.17)Введем новую переменную u по формуле u=y/x или y=ux (24.18) Поскольку в этом случае dy = udx + xdu, то уравнение (24.17) принимает вид P(l, u)dx + Q(l, u)(udx + xdu) =0, или [P(l,u) + uQ(l,u)]dx + xQ(l,u)du = 0. (24.19) Последнее уравнение является уравнением с разделяющимися переменными х, u; из него определяется u, а из формулы (24.18) - ис­комая функция у. .Если Ф(x,u,c) = 0 (24.20) - общий интеграл уравнения (24.19), то Ф(x,y/x,c)=0 (24.21) - общий интеграл уравнения (24.16).

45.Уравнение Бернулли является одним из наиболее известных нелинейных дифференциальных уравнений первого порядка. Оно записывается в виде

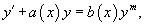
где a(x) и b(x) − непрерывные функции.

Если m = 0, то уравнение Бернулли становится линейным дифференциальным уравнением. В случае когдаm = 1, уравнение преобразуется в уравнение с разделяющимися переменными.

В общем случае, когда m ≠ 0, 1, уравнение Бернулли сводится к линейному дифференциальному уравнению с помощью подстановки

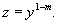
Новое дифференциальное уравнение для функции z(x) имеет вид

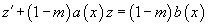
и может быть решено способами, описанными на странице Линейные дифференциальные уравнения первого порядка.