Определение числового ряда. Сходимость рядов, свойства сходящихся рядов. Необходимый признак сходимости числового ряда.

Определение. Пусть дана числовая последовательность 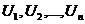,... Выражение вида (1) 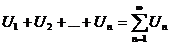называется числовым рядом. Числа 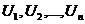называются членами ряда, число 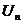– общий член ряда. Суммы конечного числа первых членов ряда 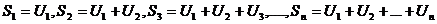называются частичными суммами ряда.

Так как число членов ряда бесконечно, то частные суммы образуют числовую последовательность .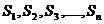

Определение. Если предел последовательности частичных сумм ряда существует и конечен, то ряд (1) называется сходящимся и сумма 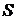ряда (1) равна пределу 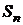: 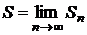. Если предел не существует или бесконечен, то ряд называется расходящимся.

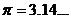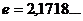Примеры. Знакомые нами числа и означают, что .

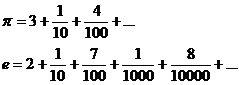По аналогии, любое десятичное разложение действительного числа представляет собой сходящийся числовой ряд, а частичные суммы 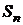– это приближенные значения числа с заданной точностью.

Рассмотрим бесконечную геометрическую прогрессию 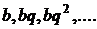, члены которой являются членами ряда 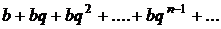. Частичная сумма этого ряда при 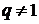имеет вид 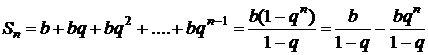. Отсюда: 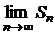= = 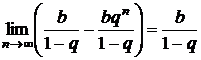, т.е. ряд сходится при 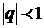и его сумма .

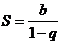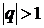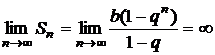При , то и ряд расходится.

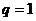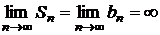Если , то и ряд расходится. При 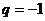ряд принимает вид 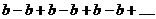. Частичные суммы ряда выглядят следующим образом 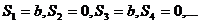. Последовательность частичных сумм ряда 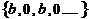предела не имеет и ряд расходится.

То есть при 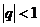ряд сходится, при 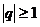– расходится.

Рассмотрим ряд 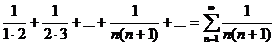. Зная, что 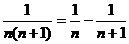имеем 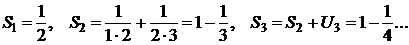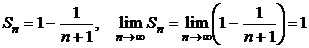. Так как 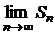существует и конечен, то ряд сходится и его сумма равна единице.

Свойства сходящихся рядов.

Если сходится ряд (1), то сходится и каждый ряд, полученный из него прибавлением или отбрасыванием конечного числа членов.

Над сходящимися рядами можно выполнять обычные арифметические действия, то есть если ряд 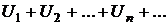сходится и его сумма равна S, и 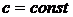, то сходится ряд 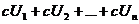и его сумма равна cS.

Пусть даны два ряда 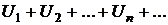и 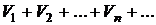. Если оба ряда сходятся, а их суммы равны соответственно S и T, то сходится ряд 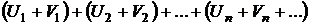и его сумма равна S+T.

Если сходится ряд (1), то сходится и каждый ряд, полученный из него группировкой слагаемых, причем суммы обоих рядов одинаковы.

При рассмотрении рядов возникают задачи: исследовать ряд на сходимость и, если он сходится, найти его сумму. В связи с этим существуют признаки сходящихся рядов.

Теорема (необходимый признак сходимости). Если ряд сходится, то предел его общего члена равен нулю.

Доказательство. Рассмотрим ряд 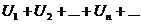. Так как 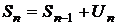, то 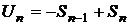. Так как по условию ряд сходится, то обе частичные суммы стремятся к S, то есть 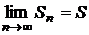и 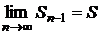, значит .

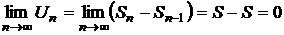Замечание. Обратное утверждение к теореме, вообще говоря неверно, то есть из того, что 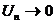ещё не следует, что ряд сходится.

С помощью теоремы можно доказать только расходимость ряда, то есть если 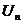не стремится к нулю, то ряд расходится. Если же 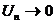, то о сходимости или расходимости ряда вывода сделать нельзя, надо проводить дополнительное исследование.

Пример. 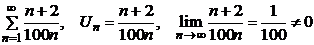– ряд расходится.

15.2. Ряды с положительными членами. Достаточные признаки сходимости положительных рядов (принцип сравнения, радикальный признак Коши, признак Даламбера). Интегральный признак Коши-Маклорена.

Определение. Ряд 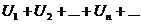называется положительным, если все его члены неотрицательны: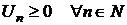

Теорема (критерий сходимости положительных рядов).

Для того, чтобы положительный ряд сходился, необходимо и достаточно, чтобы последовательность частных сумм ряда была ограничена (критерий носит теоретическое значение, и является основой, на которой базируются

другие признаки).

Достаточные признаки сходимости положительных рядов.

Признаки сравнения.

Теорема 1. Пусть члены положительных рядов 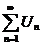(1) и 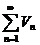(2) с вязаны соотношением 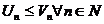, тогда из сходимости ряда (2) (большего) следует сходимость ряда (1) (меньшего); если ряд (1) (с меньшими членами) расходится, то расходится ряд (2) (с большими членами).

Теорема 2. Если предел отношения общих членов положительных рядов (1) и (2) есть конечное не равное нулю число 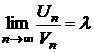, то оба ряда сходятся или расходятся одновременно.

Примечание. В качестве рядов сравнения используют эталонные ряды, о поведении которых известно:

1) ряд, составленный из членов геометрической прогрессии 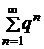, который сходится 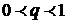, и расходится при ;

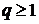2) обобщённый гармонический ряд 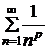с показателем сходимости р, который сходится при 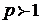, и расходится при .

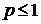Выбор одного из двух эталонных рядов для исследования неизвестного ряда определяется по виду исследуемого ряда.

Пример 1. Исследовать сходимость ряда .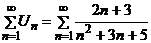

Сравним исследуемый ряд 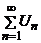с рядом 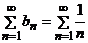, который расходится. Найдём 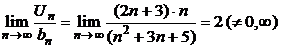, следовательно исходный ряд 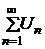расходится (на основании предельного признака сравнения).

Пример 2. Исследовать ряд .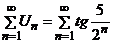

Сравним исследуемый ряд 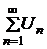с рядом 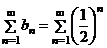, который сходится. Определим 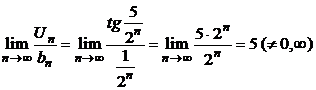, исходный ряд сходится, так как сходится ряд сравнения.

Признак Даламбера.

Пусть для положительного ряда 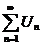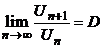, тогда при 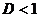ряд сходится, при D>1 ряд расходится.

Замечание. При D=1 вопрос о сходимости ряда остается открытым.

Радикальный признак Коши.

Пусть для положительного ряда 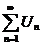, , 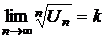тогда при k<1 ряд сходится, а при k>1 ряд расходится.

Замечание. При k=1 вопрос о сходимости ряда остается открытым.

Теорема (интегральный признак Коши-Маклорена).

Пусть функция 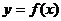удовлетворяет условиям: 1) определена и непрерывна на 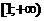; 2) 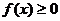; 3) монотонно убывает; 4) 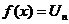. Тогда если несобственный интеграл 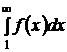сходится, то сходится ряд 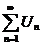; а если несобственный интеграл 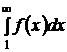расходится, то расходится ряд .

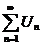Пример. Исследовать сходимость гармонического ряда .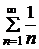

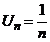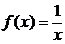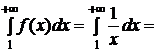
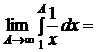
Так как , ТО И 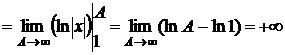. Несобственный интеграл расходится, поэтому гармонический ряд расходится.