Предел числовой последовательности.

Рассмотрим числовую последовательность 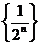. Изобразим ее на числовой оси.

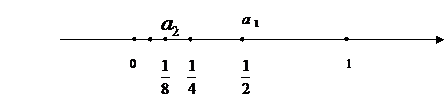
Очевидно, что члены последовательности убывают по величине, но при этом положительны и не равны нулю. При достаточно больших номерах члены последовательности будут сколь угодно близкими к 0. В этом случае говорят, что 0 является пределом данной числовой последовательности.

Опр. Число А называется пределом числовой последовательности 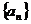, если для любого, даже сколь угодно малого положительного числа 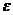, найдется такой номер N, зависящий от 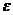, что для всех членов последовательности с номерами n>N, верно неравенство: .

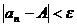Если последовательность 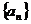имеет предел, равный А, то она называется сходящейся к числу А (в противном случае – расходящейся). Кратко это можно записать так: 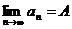. (Или так: ).

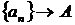Используя логические символы, определение предела числовой последовательности можно записать так:

.

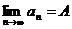
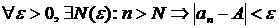Смысл определения состоит в том, что при достаточно больших номерах все члены последовательности (начиная с некоторого), будут заключены в 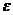- окрестности предельной точки, какой бы узкой она ни была.

Замечание. Числовая последовательность может иметь предел, равный 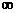, а может не иметь предела

3.Предел функции (два определения). Односторонние пределы. Бесконечные пределы.

Предел функции.

Предел функции в точке.

Односторонние пределы.

Пример.

Пусть функция y=f(x) задана в некоторой окрестности точки 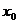, за исключением, быть может, самой точки .

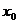Опр. 1. Точка А называется пределом функции y=f(x) при 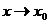, если для любой последовательности точек 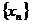, сходящейся к 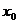, последовательность значений функции 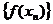сходится к А. В этом случае пишут: 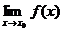=А, или 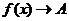при .

Это определение называют определением предела по Гейне (нем. математик XIX в.)

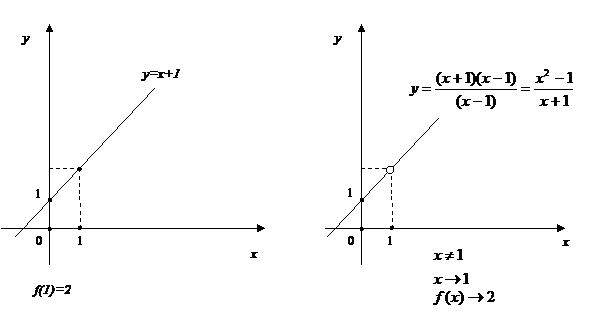
Замечание. Если точка 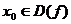, то предел 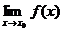, если он существует, равен значению функции в данной точке 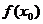. (См. рис.1)

Опр. 2. Если при стремлении к 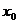x принимает лишь значения, меньшие (большие) 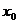, и при этом 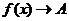, то говорят об одностороннем пределе слева 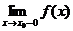(справа ).

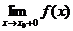Пример.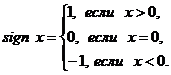

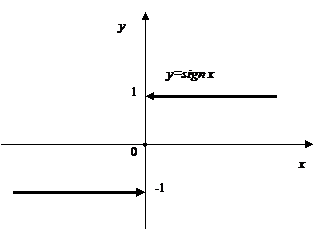
Утверждение. Предел функции в точке существует тогда и только тогда, когда существуют и равны оба односторонних предела функции в данной точке.

Бесконечные пределы.

Общее определение предела позволяет дать определение и для случаев, когда 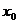или А являются несобственными точками, т.е. .

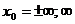Опр. 4. Число А называют пределом функции y=f(x) при 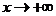и пишут 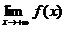=А, если:

.

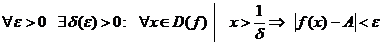Опр. 5. Число А называют пределом функции y=f(x) при 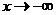и пишут 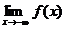=А, если:

.

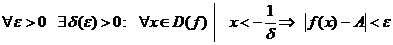Самостоятельно: сформулировать определение предела при .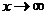

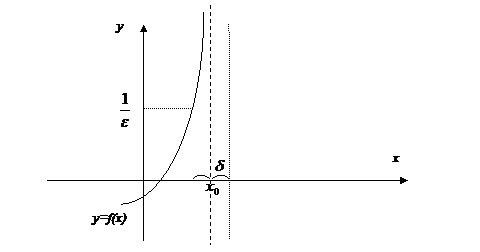
Опр.6. Говорят, что функция y=f(x) имеет предел при , равный 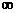и пишут 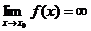, если:

.

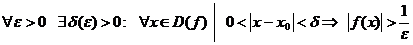4.Бесконечно малые и бесконечно большие функции, их свойства (одно с доказательством).

Опр. Функция 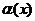называется бесконечно малой при функцией, если ее предел при равен нулю:

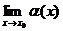=0 .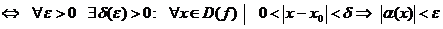

Опр. Функция 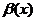называется бесконечно большой при функцией, если ее предел при есть несобственное число:

= .

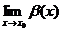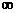
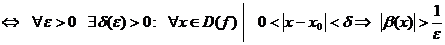Свойства