Билет 22. Признак Лейбница сходимости знакочередующихся числовых рядов.

Под знакочередующимся рядом понимается ряд, в котором члены попеременно то положительны, то отрицательны: u1-u2+u3-u4+…+(-1)^(n-1) un+..,где un>0.

Теорема (признак Лейбница):

Если члены знакочередующегося ряда

U1 – U2 + U3 – U4 + ...

монотонно убывают по абсолютной величине, т. е.

U1 ≥ U2 ≥ U3 ≥ ... ≥ Un ≥ Un+1 ≥ ... и общий член ряда стремится к нулю, lim un=0 n→∞,то:

1) ряд сходится;

2) его сумма не превосходит величины первого члена ряда

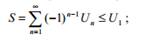
3) модуль суммы остатка ряда не превосходит абсолютной величины первого отброшен-

ного члена (первого члена остатка):

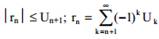и имеет знак своего первого члена.

Билет 23. Абсолютная и условная сходимости числового ряда.

Рассмотрим произвольный знакопеременный ряд

U1 + U2 + ... + Un + ... , (8.1)

т. е. ряд с членами произвольных знаков. Рассмотрим ряд, составленный из абсолютных

величин членов ряда (8.1):

|U1| + |U2| + ... + |Un| + ... . (8.2)

Теорема.

Если сходится ряд (8.2), то сходится и ряд (8.1).

Если ряд (8.1) сходится вместе с рядом (8.2), составленным из абсолютных величин

его членов, то про ряд (8.1) говорят, что он абсолютно сходится.

Если ряд (8.1) сходится и ряд (8.2) расходится, то ряд (8.1) называют условно сходящимся.

Между свойствами абсолютно и условно сходящихся рядов имеется глубокое различие.

Теорема.

Если ряд сходится абсолютно, то он остается абсолютно сходящимся при любой

перестановке его членов, причем сумма ряда не зависит от порядка его членов.

Если ряд сходится условно, то какое бы мы ни задали число А, или символ + ∞ или

– ∞, можно так переставить члены этого ряда, чтобы его сумма оказалась в точности рав-

ной А (или + ∞ или – ∞). Более того, можно так переставить члены условно сходящегося

ряда, что ряд, полученный после перестановки членов, окажется расходящимся.

Определение : ряд называется абсолютно сходящимся , если сходится как сам ряд , так и ряд, составленный из абсолютных величин его членов.

Определение: Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

Билет 24. Понятие функционального ряда, его области сходимости.

Функциональным рядом называется выражение

U1(x) + U2(x) + U3(x) + ... + Un(x) + ... ,

члены которого U1(x), U2(x), ... , Un(x), ... являются функциями от х.

Давая х числовое значение х0, мы получаем числовой ряд

U1(x0) + U2(x0) + U3(x0) + ... + Un(x0) + ... ,

который может быть как сходящимся, так и расходящимся.

Множество тех значений х, при которых функциональный ряд сходится, называет-

ся его областью сходимости. Ясно, что в области сходимости сумма функционального

ряда является некоторой функцией от х. Обозначим ее через S(x).

Специальный класс функциональных рядов составляют так называемые степенные

ряды вида

с0 + с1 х + с2 х^2+ с3 х^3+ ... + сn x^n + ... , (9.1)

где с0, с1, с2, ... , сn, ... – последовательность действительных чисел, коэффициенты ряда.

Выясним, какой вид имеет “область сходимости” степенного ряда, то есть множе-

ство {x} тех значений переменной, для которых ряд (9.1) сходится.

Теорема Абеля.

Если степенной ряд (9.1) сходится в точке х0 ≠ 0, то он сходится, и притом абсо-

лютно, в интервале (- |x0|, |x0| ), то есть при всех значениях х, удовлетворяющих условию

|x|<|x0|.

Следствие.

Если степенной ряд расходится при некотором значении х = х1, то он расходится и

при всех значениях |x|>|x1|.

Любой степенной ряд сходится при значении х=0. Есть степенные ряды, которые

сходятся только при х=0 и расходятся при остальных значениях х.

Область сходимости может состоять из всех точек оси Ох, другими словами, ряд

может сходится при всех х.

Из теоремы Абеля и ее следствия получаем, что все точки сходимости расположе-

ны от начала координат не дальше, чем любая из точек расходимости. Совершенно ясно,

что точки сходимости будут целиком заполнять некоторый интервал с центром в начале

координат.

Таким образом, можно сказать, что для каждого степенного ряда, имеющего как

точки сходимости, так и точки расходимости, существует такое положительное число R,

что для всех х, по модулю меньших R (|x|<R), ряд абсолютно сходится, а для всех х, по

модулю больших R (|x|>R), ряд расходится.