Вопрос 18. Производная по направлению. Градиент.

Пусть задана функция двух переменных u=f(x,y) (для большего числа переменных

все аналогично), которая определена в окрестности т. (x0,y0) и дифференцируема в этой

точке. Мы будем рассматривать нашу функцию на лучах, проходящих через т. (x0,y0). Луч

задается начальной точкой и направляющим единичным вектором е = {cosα,cosβ }

его параметрические уравнения имеют вид:

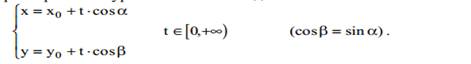
Подставляя эти выражения вместо аргументов функции u=f(x,y), мы получим

функцию одной переменной u(t): u = f(x0 + t⋅cosα, y0 + t⋅cosβ).

Если 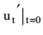существует , то эту производную 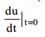мы назовем производной функции u=f(x,y) в точке (x0,y0) в направлении вектора е . Используя формулы

для производных сложной функции, получаем (для точки t=0).

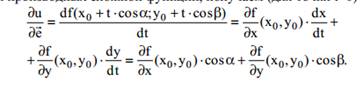
Если ввести в рассмотрение вектор 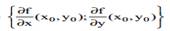(обозначаемый gradu),

то выражение для производной в направлении вектора е можно записать в виде:

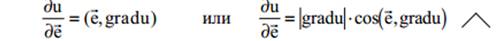
Меняя направление вектора е мы будем получать различные значения du\de.

Вопрос 19. Понятие числового ряда, его n-ой частичной суммы, сходимости числового ряда и его суммы.

Определение. Числовым рядом называется бесконечная последовательность чисел соединенных знаком сложения:

U1 +u2+u3+….+un+…=∑un. Наверху бесконеч внизу н=1.

Числа u1,u2,..,un,…называются членами ряда, а членun – общим или n-ым членом ряда.

Ряд считатется заданным, если известен его общий член un = f(n) (n=1,2,…) , т.е. задана функция натурального аргумента.

Сумма н первых членов ряда Sn называется н-й частичной суммой ряда.

Определение. Ряд называется сходящимся , если существует предел последовательности его частичных сумм, т.е. limSn = S. n→∞

Число S суммой ряда. В этом смысле можно записать : u1+u2+…+un+…=∑un=S.

Если конечного предела последовательности частичных сумм не существует, то ряд называется расходящимся.

Билет 20.Сво-ва сходящихся рядов:

1. Если ряд u1+u2+..+un+.. сходится и имеет сумму S , то и ряд λu1+λu2…. (полученный умножением данного ряда на число λ) также сходится и имеет сумму λS.

2. Если ряды u1+u2+ andv1+v2+… сходятся и их суммы соответственно равны S1 andS2 то и ряд (u1+v1)+(u2+v2)+…+(un+vn)+.. (представляющий сумму данного ряда) также сходится и его сумма равна S1+S2.

3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.

4. Для того, чтобы ряд сходился , необходимо и достаточно, чтобы при n→∞ отстаток ряда стремился к нулю, т.е. чтобы limrn = 0. При n→∞.

Билет 21. Признаки сходимости числовых рядов с положительными членами

Пусть ряд ∑An = a1+a2+…+An+… будет положительным , т.е. an>0 (n=1,2,3,...)

Тогда очевидно, An+1=An+an+1>An, т.е. Аn оказывается возрастающей. На основании

теоремы о пределе монотонной последовательности, мы непосредственно приходит к сле-

дующему основному в теории положительных рядов предложению!

Положительный ряд всегда имеет сумму; эта сумма будет конечной (и, следова-

тельно, ряд – сходящимся), если частичные суммы ряда ограничены сверху, и бесконеч-

ной (а ряд – расходящимся) в противном случае.