Производная по направлению. Градиент.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИИ ДВУХ ПЕРЕМЕННЫХ

ПЛАН

1. Полный дифференциал функции двух переменных.

2. Необходимое и достаточное условия дифференцируемости функции двух переменных.

3. Производная по направлению Градиент.

4. Частные производные и полные дифференциалы высших порядков.

1. Пусть функция z = f(х, у) определена в некоторой окрестности точки М(х, у). Составим полное приращение функции в точке М:

∆ z = f(x + ∆x, y + ∆у) – f(х, у).

Определение. Функция z = f(х, у) называется дифференцируемой(т.е.

имеет полный дифференциал) в точке М(х, у), если её

полное приращение можно представить в виде:

∆z = A · ∆x + B · ∆y + α · ∆x + β · ∆y , (1)

где α = α(∆х, ∆у) → 0 и β = β(∆х, ∆у) → 0 при ∆х → 0, ∆у → 0.

Сумма первых двух слагаемых в равенстве (1) есть выражение, линейное относительно ∆хи ∆у и представляет собой главную часть приращения функции. Сумма двух последних слагаемых правой части равенства (1) является бесконечно малой высшего порядка относительно 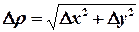, т.е. 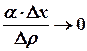или .

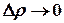Определение. Главная часть полного приращения функции z = f(х, у),

линейная относительно ∆хи ∆у, называется полным

дифференциаломэтой функции и обозначается симво-

лом dz:

dz = А · ∆х + В · ∆у. (2)

Выражения А · ∆хи В · ∆у называют частными дифференциалами.

Для независимых переменных ∆х = dхи ∆у =dу.

Поэтому равенство (2) можно записать в виде:

dz = А · dх + В · dу. (3)

Необходимое и достаточное условия дифференцируемости

Функции двух переменных.

Теорема 1 (необходимое условие дифференцируемости функции).

Если функция z = f(х, у) имеет в точке М(х, у) полный дифферен-

циал, то она имеет в этой точке частные производные и при этом

.

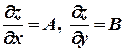Формула (3) принимает вид:

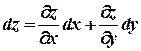. (4)

Теорема 2 (достаточное условие дифференцируемости функции).

Если функция z = f(х, у) имеет в точке непрерывные частные произ-

водные 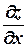и 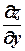, то она дифференцируема в этой точке и её пол-

ный дифференциал выражается формулой (4).

Правила и формулы вычисления дифференциалов функции одной переменной справедливы и для дифференциалов функции двух (и большего числа) переменных.

Производная по направлению. Градиент.

Пусть функция 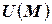, где точка М=(x,y) непрерывна и имеет непрерывные частные производные по двум переменным. Пусть задан вектор 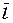(определено направление 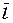). Рассмотрим точку 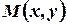, лежащую на 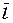, и точку 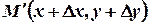также расположенную на 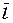. Функция 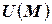при перемещении М в положение 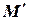получит приращение

.

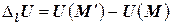Обозначим через .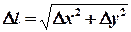

Предел

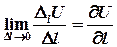
называют производной функции 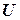по направлению 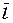и обозначают .

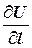ТЕОРЕМА (о вычислении производной функции по заданному направлению)

Если 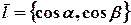и функция 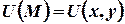непрерывна вместе со своими частными производными, тогда справедливо равенство:

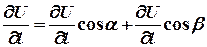. (5)

Заметим, что частные производные 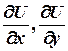являются частным случаем производной по направлению.

Производная 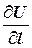характеризует скорость изменения функции 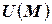по направлению вектора .

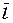Определение. Пусть задана функция 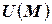в области 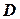. Вектор

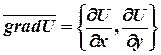
называют градиентомфункции .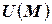

ТЕОРЕМА (о связи градиента с производной по направлению).

Пусть задана функция 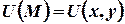. Производная 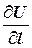по направлению некоторого вектора 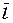равна проекции вектора 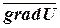на вектор 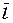, то есть 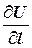можно вычислить по формуле

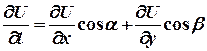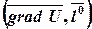= . (6)

В правой части формулы (6) стоит скалярное произведение двух векторов: вектора 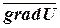и единичного вектора 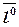заданного направления .

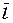Как известно из курса аналитической геометрии, единичный вектор вектора 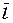можно найти по формуле

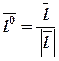. (7)

Координатами единичного вектора 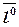являются направляющие косинусы заданного направления 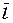, т.е. .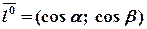