Производная по направлению, градиент

Пусть мы снова рассматриваем график функции 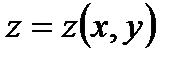и сечения этой поверхности плоскостями, проходящими через точку 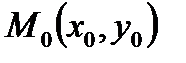плоскости OXY и параллельными оси Z. В сечениях получаются кривые, проходящие через точку 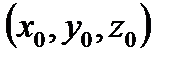. Проекция такой кривой на плоскость OXY есть прямая линия, проходящая через точку 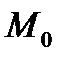. Будем обозначать направляющий вектор этой прямой через 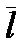, а точки прямой – буквами М. Введём понятие величины отрезка :

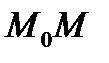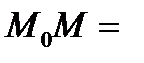длине отрезка 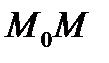со знаком “+”, если 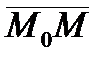и и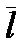меют одинаковые направления;

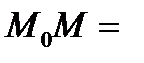длине отрезка 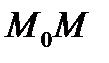со знаком “-”, есл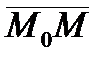и и 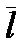имеют разные направления;

Предположим теперь, что мы рассматриваем некоторую плоскость, на ней фиксируем точку 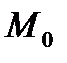и направление 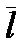. Пусть для этой точки плоскости определена величина 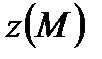- функция от точки М.

Важно отметить, что пока мы не вводим никакой системы координат (точки на плоскости, направления и функции от точек можно определить без системы координат). Например, температуру воздуха в данной точке обычно измеряют термометром, при этом, не особенно задумываясь о системе координат в пространстве. Направление тоже часто указывают без всяких координат (например, пальцем, что не служит признаком хорошего воспитания) и т.д.

Рассмотрим теперь точки М, лежащие на прямой, проходящей через 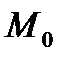в указанном направлении 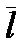и соответствующую величину 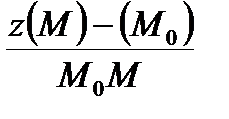; если существует предел этой величины при стремлении М к М₀ вдоль прямой, то он называется производной z(M) в точке M₀ по направлению 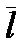и обозначается 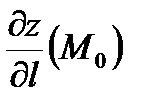. Как мы видим, в определении производной по направлению координаты не участвовали. Однако для получения простой формулы для вычисления этой производной удобно ввести систему координат. Итак, пусть 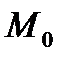имеет координаты 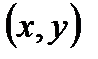, М – координаты 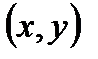, 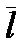имеет координаты 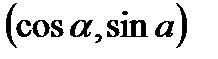. Тогда вводя параметризацию 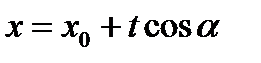, , 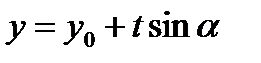для прямой, соединяющей М₀ с М, М₀М=t , получаем: 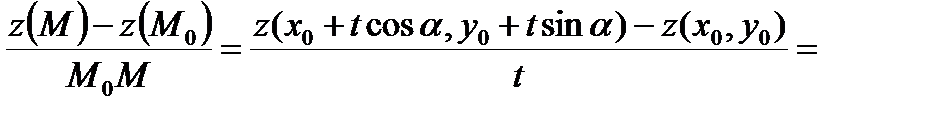(т. к. мы предположили, что z – дифференцируема в )

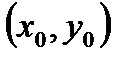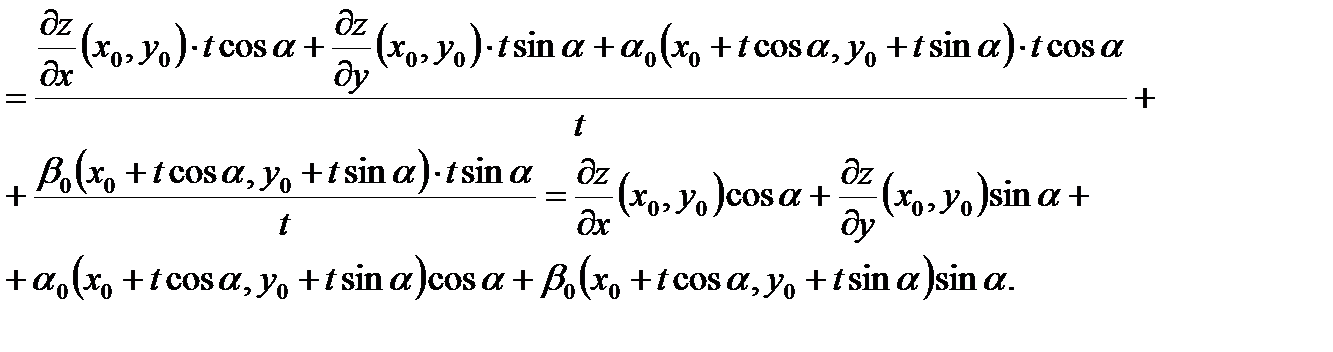
Пр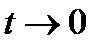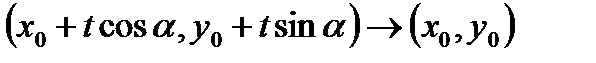и и 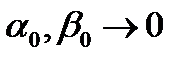. Поэтому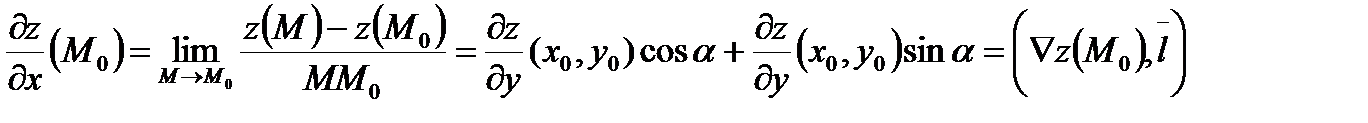

Аналогично, в случае 3-х переменных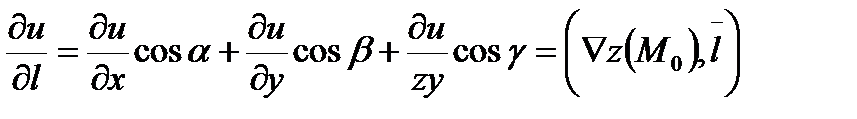

Скалярное произведение в правых частях или можно представить, как 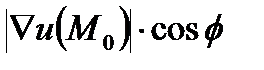(поскольку 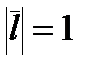), где 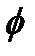- угол между 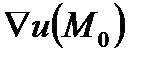и заданным направлением .

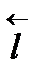Мы видим, что это выражение имеет наибольшую величину, когда 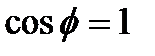. Это позволяет определить градиент, как вектор, модуль которого равен наибольшей из величин производных по направлению в этой точке. А направление его как раз такое, в котором производная достигает наибольшей величины. Это определение градиента, в котором не участвуют координаты, позволяет рассматривать его как характеристику функции, не зависящую от наблюдателя.

Установим ряд важных свойств градиента: пусть 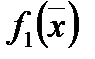и 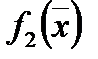имеют все частные производные 1-го порядка. Тогда

1. ;

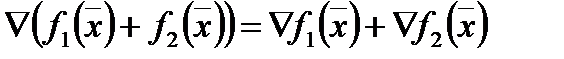2. ;

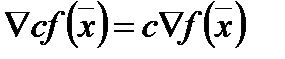3. ;

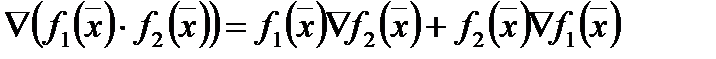4. Если 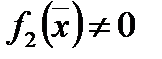, то ;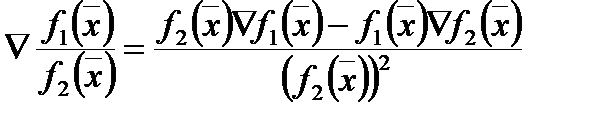

5. Если 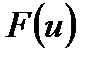- функция одной переменной, имеющая производную, то .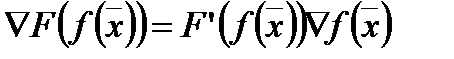