Предел функции и его свойства.

Определения:

Рассмотрим функцию 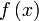, определённую на некотором множестве 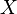, которое имеет предельную точку 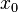(которая, в свою очередь, не обязана ему принадлежать).

Значение 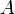называется пределом (предельным значением) функции 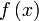в точке 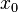, если для любой последовательности точек 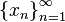, сходящейся к 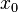, но не содержащей 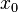в качестве одного из своих элементов (то есть в проколотой окрестности 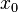), последовательность значений функции 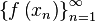сходится к 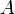.^[1]

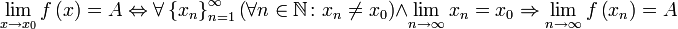
Эквивалентность определений

Все данные выше определения предела функции в точке эквивалентны.^[1] Иными словами, из любого из них можно вывести любое другое, то есть выполнение одного из них неизбежно влечёт выполнение всех остальных.

Свойства пределов числовых функций

Пусть даны функци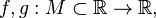и и .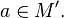

· Одна и та же функция в одной и той же точке может иметь только один предел.

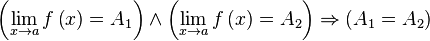
Доказательство

· Сходящаяся функция локально сохраняет знак. Более обще,

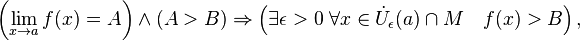
где 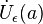— проколотая окрестность точки .

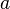· В частности, функция, сходящаяся к положительному (отрицательному) пределу, остаётся положительной (отрицательной) в некоторой окрестности предельной точки:

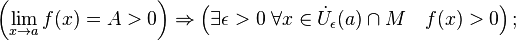
· Сходящаяся функция локально ограничена в окрестности предельной точки:

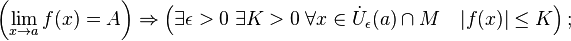
· Отделимость от нуля функций, имеющих предел, отличный от нуля.

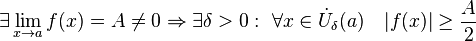
· Операция взятия предела сохраняет нестрогие неравенства.

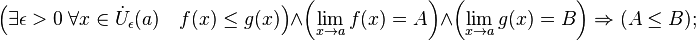
· Правило двух милиционеров

· Предел суммы равен сумме пределов:

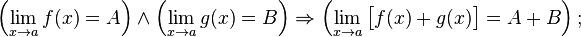
· Предел разности равен разности пределов:

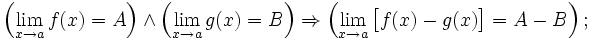
· Предел произведения равен произведению пределов:

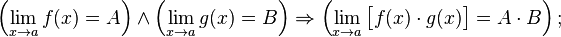
· Предел частного равен частному пределов.

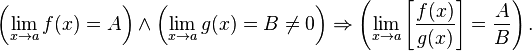
Непрерывные функции и их свойства. Точка разрыва функции и их классификация.

Непрерывная функция — функция без «скачков», то есть такая, у которой малые изменения аргумента приводят к малым изменениям значения функции.

Непрерывная функция, вообще говоря, синоним понятия непрерывное отображение, тем не менее чаще всего этот термин используется в более узком смысле — для отображений между числовыми пространствами, например, на вещественной прямой. Эта статья посвящена именно непрерывным функциям, определённым на подмножестве вещественных чисел и принимающим вещественные значения.

Определение

Пусть 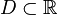и .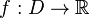

Функция 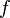непрерывна в точке 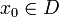, если для любого 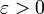существует 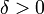такое, что для любого

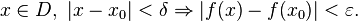
Функция 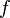непрерывна на множестве 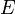, если она непрерывна в каждой точке данного множества.

В этом случае говорят, что функция 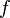класса 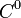и пишут: 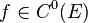или, подробнее, .

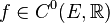Комментарии

· Определение непрерывности фактически повторяет определение предела функции в данной точке. Другими словами, функция 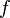непрерывна в точке 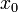, предельной для множества 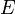, если 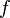имеет предел в точке 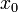, и этот предел совпадает со значением функции .

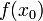· Функция непрерывна в точке, если её колебание в данной точке равно нулю.

Точки разрыва

Если условие, входящее в определение непрерывности функции в некоторой точке, нарушается, то говорят, что рассматриваемая функция терпит в данной точке разрыв. Другими словами, если 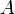— значение функции 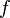в точке 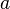, то предел такой функции (если он существует) не совпадает с 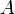. На языке окрестностей условие разрывности функции 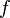в точке 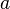получается отрицанием условия непрерывности рассматриваемой функции в данной точке, а именно: существует такая окрестность точки 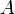области значений функции 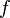, что как бы мы близко не подходили к точке 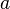области определения функции 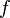, всегда найдутся такие точки, чьи образы будут за пределами окрестности точки .

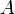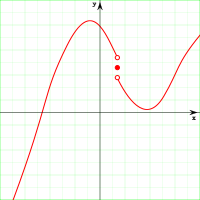
Устранимые точки разрыва

Если предел функции существует, но он не совпадает со значением функции в данной точке:

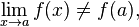
тогда точка 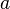называется точкой устранимого разрыва функции 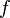(в комплексном анализе — устранимая особая точка).

Если «поправить» функцию 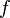в точке устранимого разрыва и положить 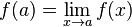, то получится функция, непрерывная в данной точке. Такая операция над функцией называется доопределением функции до непрерывной или доопределением функции по непрерывности, что и обосновывает название точки, как точки устранимого разрыва.