Уравнения прямой на плоскости

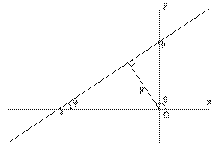
Способы задания прямой:
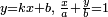или .

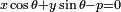Общее уравнение прямой

Общее уравнение прямой линии на плоскости в декартовых координатах:

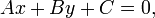
где A, B и C — произвольные постоянные, причем постоянные A и B не равны нулю одновременно. Вектор с координатами (A,B) называется нормальным вектором и он перпендикулярен прямой. Вектор с координатами (-B,A) или (B,-A) называется направляющим вектором.

При C = 0 прямая проходит через начало координат. Также уравнение можно переписать в виде :

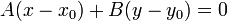
Уравнение прямой, проходящей через точку c координатами (х₀;у₀) с известным угловым коэффициентом:

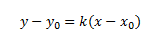
Уравнение прямой проходящей через две точки:

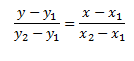
Уравнение прямой в отрезках на координатных осях:

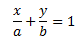
Расстояние от точки c координатами (х₀;у₀) до прямой Ах+Ву+С=0:

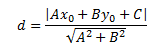
Уравнение прямой, проходящей через две точки

Пусть в пространстве заданы две точки M ₁ ( x ₁ , y ₁ , z ₁ ) и M₂ ( x ₂, y ₂ , z ₂ ), тогда уравнение прямой, проходящей через эти точки:

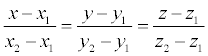
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.

На плоскости записанное выше уравнение прямой упрощается:

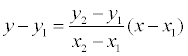
если х ₁ ≠ х₂ и х = х ₁ , если х ₁ = х₂ .

Дробь 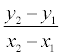= k называется угловым коэффициентомпрямой.

Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).

Применяя записанную выше формулу, получаем:

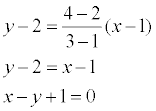
Уравнение плоскости

Рассмотрим произвольную точку 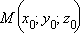в пространстве и некоторый вектор 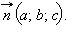Очевидно, что геометрическим местом точек 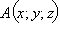таких, что вектор 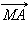перпендикулярен вектору 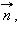будет плоскость, проходящая через точку M перпендикулярно прямой, для которой вектор 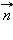является направляющим. Нашей задачей будет установить уравнение плоскости, то есть найти соотношение, которому удовлетворяют координаты точки A.

Запишем условие перпендикулярности векторов с использованием скалярного произведения:

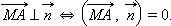Запишем последнее равенство в координатах:

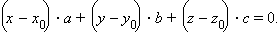Поскольку все наши выкладки были равносильными, то это и есть уравнение плоскости, проходящей через заданную точку. Преобразуем его к виду

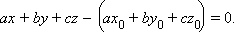Обозначая 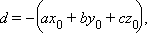получим

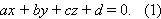Это и есть так называемое общее уравнение плоскости. Вектор 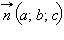называется нормальным вектором (или просто нормалью) для плоскости, заданной общим уравнением (1).

Нормальный вектор к плоскости перпендикулярен ей, что следует из самого вывода уравнения плоскости.

Уравнение плоскости, проходящей через три данные точки

Пусть плоскость задана тремя точкам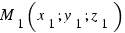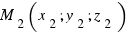и: , и 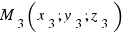. тогда уравнение имеет вид:

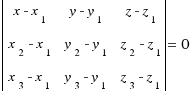
23)Каноническим уравнением прямой называют уравнение

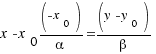
Термины направляющий вектор и начальная точка вводятся для канонического уравнения так же, как и для параметрического уравнения (и имеют тот же смысл).

Каноническое уравнение прямой в пространстве Каноническое уравнение прямой в пространстве имеет вид:

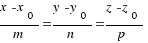
Где, 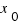, , 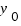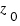- координаты точки, лежаей на плоскости, а m, n и p - координаты направляющего вектора прямой.

Числовые последовательности

Если каждому числу n из натурального ряда чисел: 1, 2, 3, …, n, … поставлено в соответствие вещественное число x_n, то множество вещественных чисел x₁, x₂, …,x_n, … называется числовой последовательностью или просто последовательностью.
Числа x₁, x₂, x₃, …, x_n,… будем называть элементами (или членами) последовательности, x_n = f (n) – формула, по которой находится каждый член последовательности, называется общим членом последовательности. Сокращенно последовательность будем обозначать символом { x_n } Примеры числовых последовательностей

• 1)
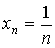
• 2)
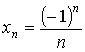
• 3) a_n = a₁ + (n - 1)·d – арифметическая прогрессия,
• 4) x_n = x₁·q^{n - 1}– геометрическая прогрессия,
• 5) x_n = τ (n) – число делителей числа n,
• 6) x_n = n !

Последовательность считается заданной, если указан способ получения любого ее элемента. Последовательность можно задать соотношением между двумя последовательными членами последовательности. К примеру, арифметическую прогрессию можно задать соотношением a_n = a_n-1 + d, начиная со второго члена. По самому определению, последовательность содержит бесконечное число элементов, любые два ее элемента отличаются, по крайней мере, своими номерами.