Предел последовательности и его свойства.
Определение. Пусть (xn) = {x1,x2,x3...xn} –некоторая числовая последовательность.
Говорят, что число а является пределом последовательности, если для любого e>0 существует N=N(e) такой, что при всех n>N выполняется |xn-a|<e
В этом случае этот факт записывают 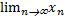 = a
= a
Последовательность, имеющая предел называется сходящейся, в противном случае – расходящейся. Последовательность называется бесконечно малой, если ее предел равен нулю.
Определение. Говорят, что последовательность имеет своим пределом +¥(-¥_ и пишут 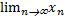 = +¥ (
= +¥ ( 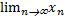 = -¥) если для любого числа Е>0 существует N=N(E) – такой номер, что при всех n>N выполняется xn>E (xn<-E)
= -¥) если для любого числа Е>0 существует N=N(E) – такой номер, что при всех n>N выполняется xn>E (xn<-E)
Последовательность xn называется ограниченной, если существует M>0 такое что |xn|<M при всех nÎN.
Теорема 1.
1. Любая окрестность предела последовательности содержит все члены последовательности, за исключением конечного их числа.
2. Последовательность не может иметь двух раздичных пределов.
3. Любая сходящаяся последовательность ограничена.
Теорема 2.
Пусть 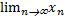 =А
=А 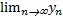 =B
=B
Тогда:
1. 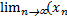 +yn) = A+B
+yn) = A+B
2. 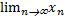 yn = AB
yn = AB
3. 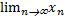 /yn = A/B если В¹0
/yn = A/B если В¹0
Последовательность xn – убывающая, если xn> xn+1 при всех nÎN. И невозрастающая, если xn>= xn+1 при всех nÎN. Возрастающая xn< xn+1. Неубывающая xn<= xn+1
Убывающая, невозрастающая, возрастающая, неубывающая последовательности называются монотонными.
Теорема. Любая ограниченная монотонная последовательность сходится (имеет предел).
ЧИСЛО Е.
Неравенство Бермули (1+a)n>= 1+na, a>-1
Теорема. Последовательность xn = (1+1/n)n сходится, т.е. имеет предел.
Доказательство:
Рассмотрим

Ясно также, что yn>0 при всех nÎN, т.к. yn ограничена.
По предыдущей теореме
Пределом xn = (1+1/n)n называется число е = 2,718281828459045
е играет огромную роль в анализе, а сам предел называется вторым замечательным пределом. Логарифм по основанию числа е называют натуральным логарифмом.
ПРЕДЕЛ ФУНКЦИИ В ТОЧКЕ, БЕСКОНЕЧНОСТИ. ОДНОСТОРОННИЕ ПРЕДЕЛЫ.
Пусть f(x) – некоторая ф-я, x0ÎR
Определение: число А называется пределом функции f(x) в точке x0 , если для любой последовательности xn , сходящейся к x0 ( 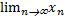 = x0 ) соответствующая последовательность значений функции f(xn ) сходится к А.
= x0 ) соответствующая последовательность значений функции f(xn ) сходится к А.
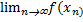 = A
= A
Определение. Число А называется пределом функции в ¥(-¥) если для любого e>0 существует D = D(e)>0 такое, что при всех x>D (x< -D) выполняется неравенство |f(x) – A|<e
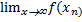 = A (
= A ( 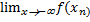 = A)
= A)
Определение. Говорят, что в точке x0 функция f(x) имеет своим пределом +¥(-¥) если для любого Е>0 существует d=d(E)>0 такое, что при всех xÎ( x0-d, x0+d) выполняется f(x)>E (f(x)<-E)
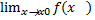 = +¥(-¥)
= +¥(-¥)
Односторонние пределы.
Определение. Число А называется левосторонним (пределом слева) пределом функции f(x) в точке x0 если "e>0 $d=d(e)>0 такое, что при всех хÎ( x0 -d, x0) выпоняется |f(x) – A|<e
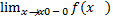 = A.
= A.
Аналогично – правосторонний предел. хÎ( x0, x0+d), |f(x) – A|<e
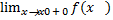 = A.
= A.

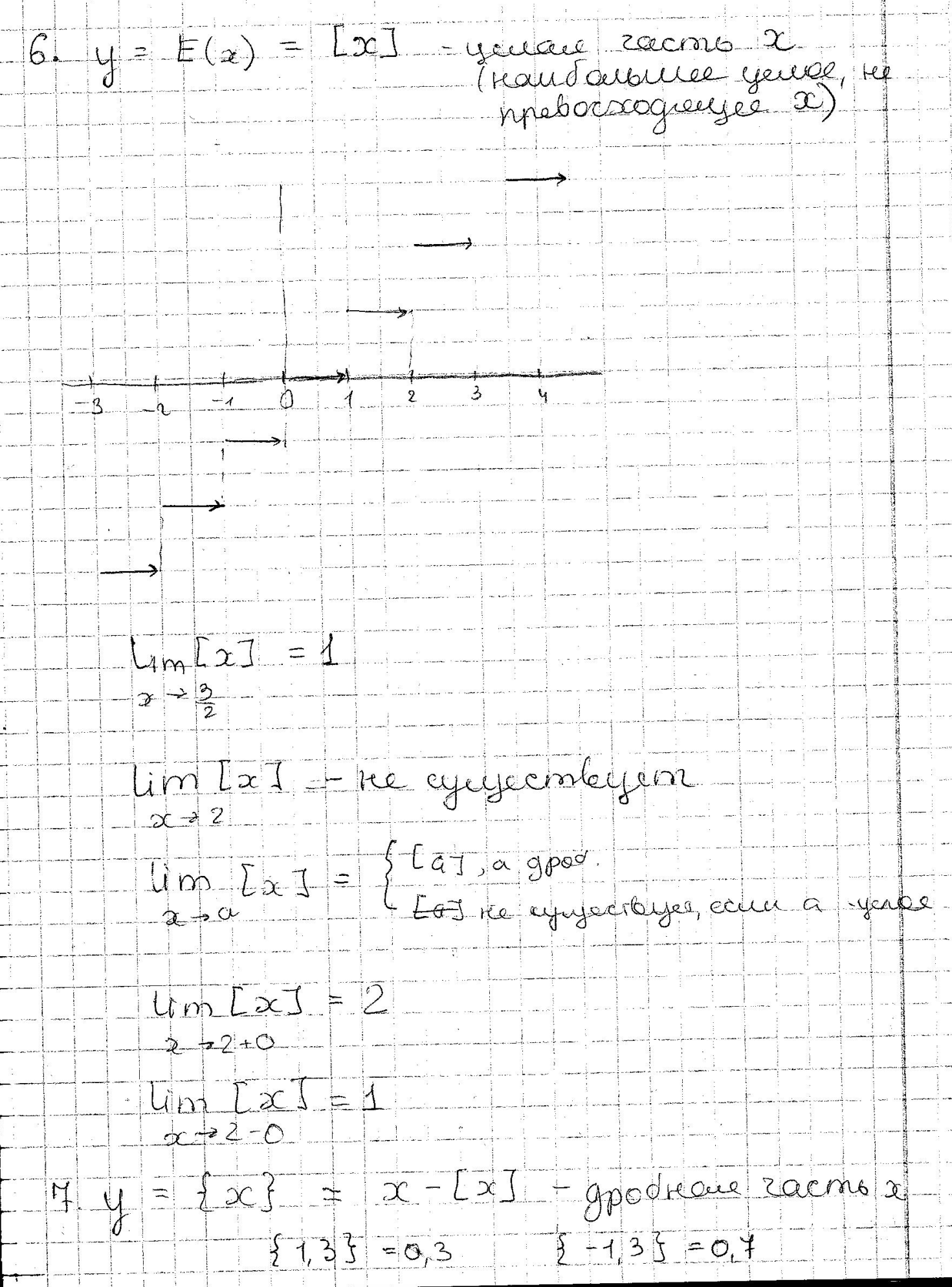
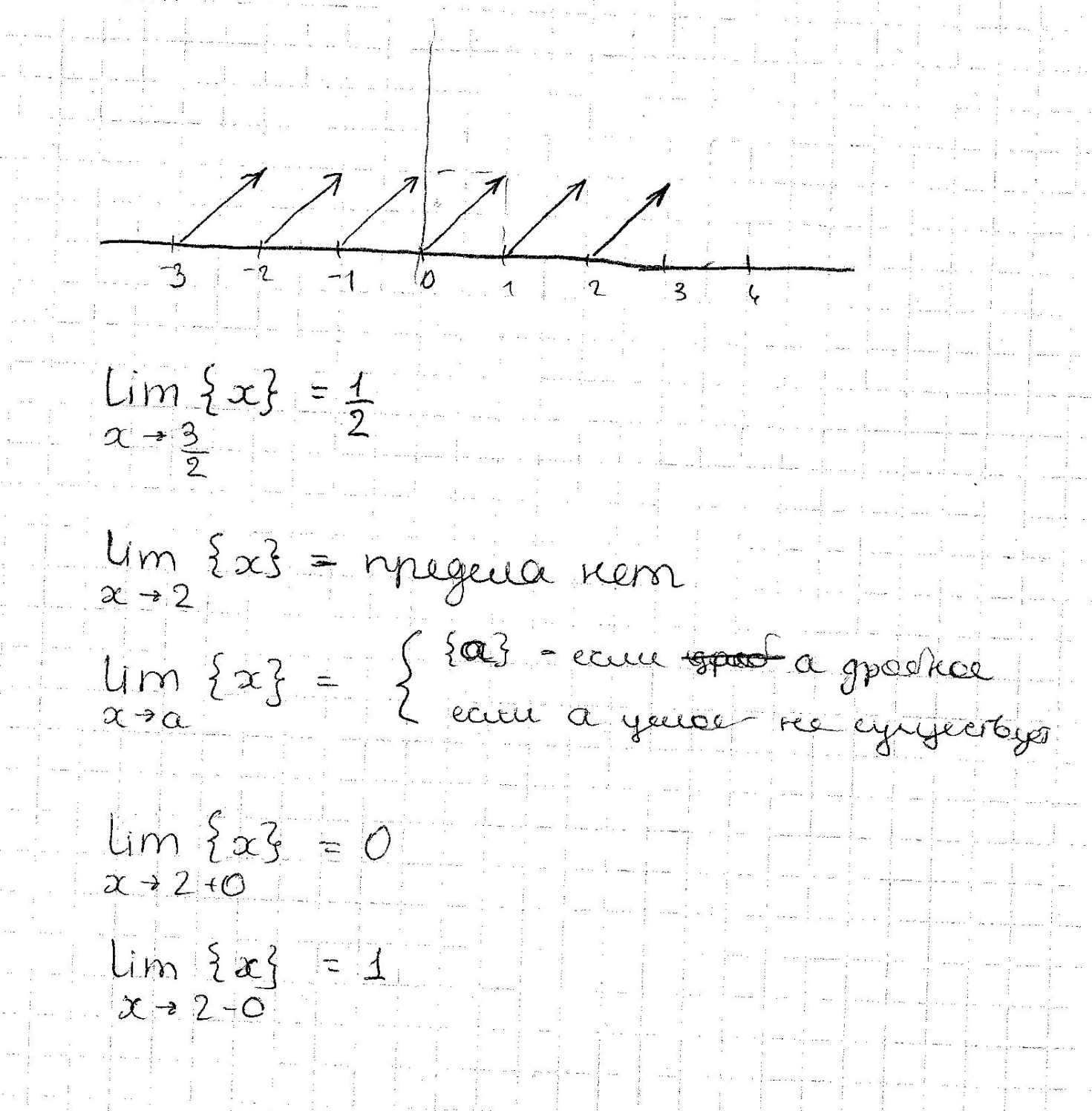
ТЕОРЕМЫ О ПРЕДЕЛАХ ФУНКЦИИ.
Теорема1. Для существования предела ф-ии f(x) в точке x0 необходимо и достаточно существование обоих односторонних пределов в этой точке и их равенство.
Теорема2. Если функция f(x) и g(x) определены в некоторой окрестности точки x0 и для всех xÎO(x0) имеет место неравенство f(x)<=g(x), то limx->x0f(x)<= limx->x0g(x) если они существуют.
Теорема3. Пусть в окрестности точки x0 – O(x0) определены ф-ии f(x), j(x), y(x) и f(x)£ j(x)£ y(x)
Предположим, что существует 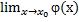 =
= 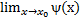 =A
=A
Тогда существует 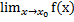 = A
= A
Теорема4. Пусть 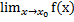 = A и
= A и 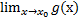 = B
= B
Тогда:
1. 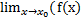 ±
± 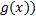 = A ± B
= A ± B
2. 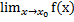 g(x) = AB
g(x) = AB
3. 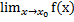 /g(x) = A/B, B¹0
/g(x) = A/B, B¹0
- lim сf(x) = c lim f(х), если с – const, постоянную величину можно вынести за знак предела;
- lim хn = (lim x)n:
- lim nÖx = nÖlim x.
