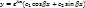Однородные дифференциальные уравнения первого порядка

Ф-я f(x, y) называется однородной n – го измерения относительно своих аргументов х и у, если для любого значения параметра t (кроме нуля) выполняется тождество: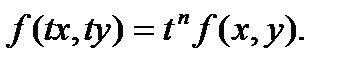

ДУ вида 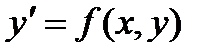наз-ся однородным, если его правая часть f(x, y) есть однородная функция нулевого измерения относительно своих аргументов.

Любое уравнение вида 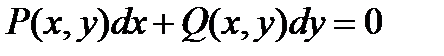является однородным, если функции P(x, y) и Q(x, y) – однородные функции одинакового измерения.

Решение любого однородного уравнения основано на приведении этого уравнения к уравнению с разделяющимися переменными.

Рассмотрим однородное уравнение 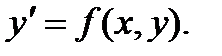Т.к. функция f(x, y) – однородная нулевого измерения, то можно записать: 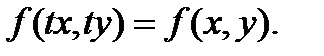Т.к. параметр t вообще говоря произвольный, предположим, что 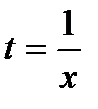. Получаем: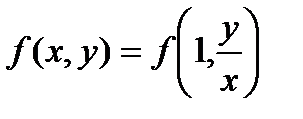

Правая часть полученного равенства зависит фактически только от одного аргумента 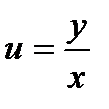, т.е.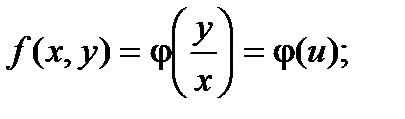

Исходное дифференциальное уравнение таким образом можно записать в виде: 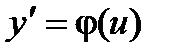. Далее заменяем y = ux, .

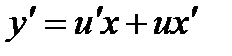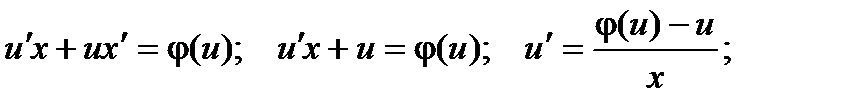
таким образом, получили уравнение с разделяющимися переменными относительно неизвестной функции u.

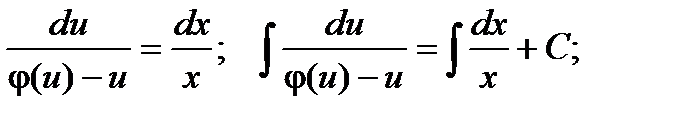
Далее, заменив вспомогательную функцию u на ее выражение через х и у и найдя интегралы, получим общее решение однородного дифференциального уравнения.

51. Линейные ДУ 1 порядка.

Дифференциальным уравнением наз соотношение, связывающее независ переменную x, искомую ф-ию y=f(x) и её производную.

Если искомая функция есть ф-ия одной независимой переменной, то ДУ наз обыкновенным, порядок старшей производной , входящей в ДУ, наз порядком данного ур-я.

Общий вид ДУ n-го порядка: (1)

Ф-ия y=f(x), кот-я при подстановке в ур-е (1) обращает этоур-е в тождество, наз-ся решением этого ур-я.

ДУ 1-го порядка имеет вид: F(x,y,y’)=0 (2) или y’=f(x,y)(3) в случае, если y’ можно выразить относительно x и y

Реш-е ур-я (3) наз-ся общим реш-ем этого ур-я.

Реш-е может получаться в неявной форме Ф(x,y,c)=0 – наз общим интегралом.

Реш-е, кот получается из общего при некотором фиксированном значении С наз частным решением. Условия, что при x=x₀ ф-ия y=y₀ наз начальным условием, кот-е позволяет из общего реш-я выделить частное.

Ур-я с разделяющимися переменными.

Ур-е вида наз ур-ем с разделяющимися переменными. Это ур-е можно записать в виде: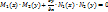

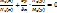, домножим на p wsp:rsidR="00000000" wsp:rsidRDefault="000D1362"><m:oMathPara><m:oMath><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="10"/><w:sz-cs w:val="10"/></w:rPr><m:t>в?‚x</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1417" w:right="1417" w:bottom="1417" w:left="1417" w:header="708" w:footer="708" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> :

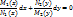
Вычислим: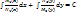

Однородные ДУ

Ф-ия f(x,y) наз однородной измерения М если имеет место тождество f(xt,yt)=t^m(x,y)

f(x,y) = x²-3xy+2y²

f(tx,ty)=(tx)²-3(tx)(ty)+2(ty)²=t²(x²-3xy+2y²)=t²f(x,y) – однородная ф-ия измерения t.

Ур-е M(x,y)dx+N(x,y)dy=0 наз однородным ДУ 1-го порядка, если ф-ии M и N однородные ф-ии одного и того же измерения.

С помощью подстановки y=ux, где u – искомая ф-ия, зависящая от x, ур-е сводится к ур-ю с разделяющимися переменными.

ДУ второго порядка

Общий вид: F(x,y,y’,y’’)=0. Общее реш-е содержит 2 независимые произвольные постоянные с₁ и с₂. Если заданы начальные условия y(x₀)=y₀, y’(x₀) = y’₀, то из с-мы 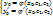можно найти произв постоянные с₁ и с₂, тем самым найти частное реш-е

Ур-я 2-го порядка решаются путём применения неопределённого интегрирования в след случаях:

1. Пусть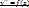

; ; ;

;

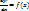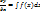+c

2.

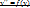
Положим , тогда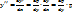

=> данное ур-е примет вид: 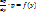, те получаем ур-е 1-го порядка с разделяющимися переменными.

Однородные линейные ДУ 2-го порядка имеет вид: ; p,q – нек действительные числа.

Искать решение в виде

λ²+pλ+q=0 – характеристическое ур-е.

1 случай: ур-е имеет 2 действит корня, λ₁≠ λ₂, тогда общее реш-е имеет вид: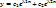

2 случай: ур-е имеет 2 действит совп корня λ₁= λ₂= λ

Общее реш-е:

3 случай: корни квадратного ур-я мнимые: λ_1,2= ,

Общий вид: