Уравнение плоскости в отрезках.

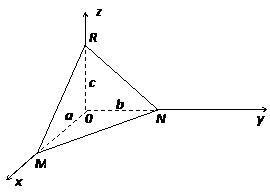
Пусть плоскость не проходит через начало координат, а отсекает от осей координат соответственно отрезки a, b, c. Как видно из рисунка 4.10, плоскость проходит через точки M(a,0,0), N(0,b,0) и R(0,0,c).

Рисунок 4.10

Пусть общее уравнение плоскости имеет вид: Ax + By + Cz + D = 0 (4.31). Подставим в это уравнение координаты точек M, N и R, получим:

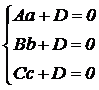(4.34)

Так как плоскость не проходит через начало координат, то D≠ 0. Так как плоскость отсекает от осей координат ненулевые отрезки, то A≠ 0, B≠ 0, C≠ 0. Тогда из (4.34) имеем: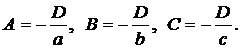

Подставив эти значения в уравнение (4.31), получим: .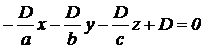

Так как D≠0, то все члены последнего равенства можно разделить на (-D). Получим:

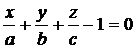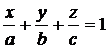или (4.35)

Уравнение (4.35) и есть уравнение плоскости в отрезках.

ВВЕДЕНИЕ В АНАЛИЗ.

Предел числовой последовательности.

Если по некоторому закону каждому натуральному числу n поставлено в соответствие вполне определенное число a_n , то говорят, что задана числовая последовательность 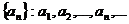. Другими словами, числовая последовательность – это функция натурального аргумента: a_n=f(x). Числа 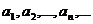называются членами последовательности, а число a_n – общим или n-ым членом данной последовательности.

Можно заметить, что члены последовательности a_n с ростом n как угодно близко приближаются к 1. при этом абсолютная величина разности 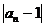становится все меньше и меньше. Действительно: 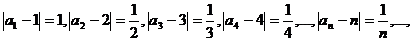т.е с ростом n 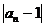будет меньше сколь угодно малого положительного числа.

Число A называется пределом числовой последовательности 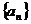, если для любого даже сколь угодно малого положительного числа e>0 найдется такой номер N( зависящий от e, N=N(e)), что для всех членов последовательности с номерами n>N верно неравенство: 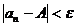(6.2).

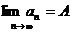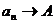Предел числовой последовательности обозначается или при 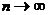. Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.

Смысл определения предела числовой последовательности состоит в том, что для достаточно больших n члены последовательности 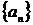как угодно мало отличаются от числа А. Важно отметить, что номер N, вообще говоря, не может быть указан раз и навсегда: он зависит от выбора числа 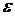. При уменьшении 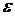, соответствующий номер Ne, вообще говоря увеличивается.

Для геометрической интерпретации понятия предела числовой последовательности распишем неравенство:

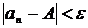(1) ,

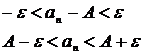
Изобразим числа А, А + e, А-e и значение 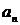точками на числовой оси. Получим наглядно геометрическое истолкование предела последовательности:

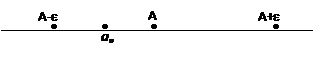
Какой бы малый отрезок (длины 2e) с центром в точке А ни взять, все точки 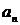начиная с некоторой из них должны попасть внутрь этого отрезка (так, что вне его может остаться лишь конечное число этих точек).

Теоремы о пределах (вывод одной из них).

Теорема 1. Для того, чтобы число A было пределом функции f(x) при x®a, необходимо и достаточно, чтобы эта функция была представлена в виде: f(x) = A+a(x), где a(x) – бесконечно малая функция.