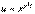Производная по направлению. Градиент функции.

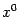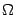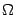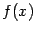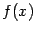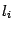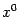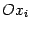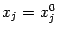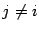Пусть -- внутренняя точка области , и в области задана функция . Рассмотрим ограничение функции на прямую , проходящую через точку параллельно оси . Эта прямая задаётся условиями при ; переменная 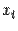может при этом произвольно меняться. Поэтому для рассматриваемого ограничения 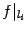имеется естественная параметризация, смысл которой в том, что "замораживаются" все переменные, от которых зависит 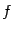, кроме :

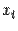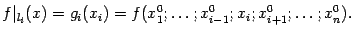
Получили функцию одного переменного 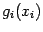, как параметризацию ограничения с помощью параметра .

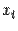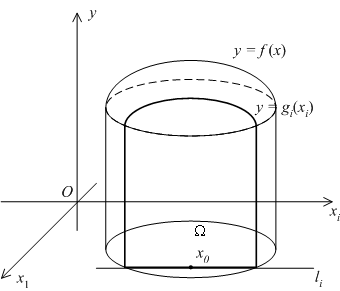
Рис.7.12.

Функция 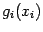может иметь производную в точке 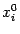, равную некоторому числу 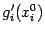. Это число называют частной производной функции 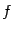по переменной 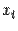, вычисленной в точке 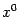. Эта частная производная обозначается 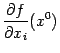или .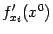

Сразу же заметим, что значения частных производных от функции 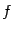в точке 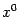, вычисленные по разным переменным 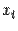и 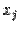, могут быть различными, так что обозначение типа 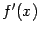, без указания переменной, по которой вычислена частная производная, не имеет смысла: в обозначении обязательно нужно указывать переменную, по которой мы дифференцируем.

Итак, чтобы вычислить частную производную от функции 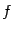по некоторой переменной 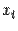, нужно фиксировать значения всех переменных, кроме 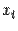(то есть временно считать их постоянными), а затем по обычным правилам вычисления производных найти производную по этой единственной переменной 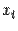. Теперь ясно, что для вычисления частных производных никаких новых правил дифференцирования вдобавок к тем, что известны нам для функций одной переменной, не потребуется, ведь при вычислении частной производной мы считаем, что может изменяться только одна переменная. Считая точку 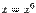, в которой вычисляется значение частной производной 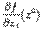, переменной точкой области 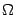и предполагая, что во всех точках 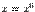эта производная существует, мы получаем, что частная производная 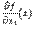-- это функция, заданная в области 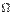(или в её части, если производная существует не везде в 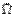). Производные и дифференциалы функций нескольких переменных.Определение. Пусть в некоторой области задана функция z = f(x, y). Возьмем произвольную точку М(х, у) и зададим приращение Dх к переменной х. Тогда величина D_xz = f( x + Dx, y) – f(x, y) называется частным приращением функции по х.

Можно записать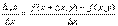

Тогда 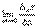называется частной производнойфункции z = f(x, y) по х.

Обозначение: 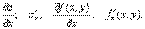Аналогично определяется частная производная функции по у. 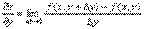Геометрическим смысломчастной производной (допустим 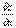) является тангенс угла наклона касательной, проведенной в точке N₀(x₀, y₀, z₀) к сечению поверхности плоскостью у = у₀.

Полное приращение и полный дифференциал.

Определение. Для функции f(x, y) выражение Dz = f( x + Dx, y + Dy) – f(x, y) называется полным приращением.

Если функция f(x, y) имеет непрерывные частные производные, то

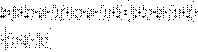Применим теорему Лагранжа к выражениям, стоящим в квадратных скобках.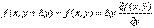 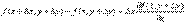здесь

Тогда получаем 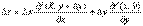Т.к. частные производные непрерывны, то можно записать равенства: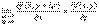

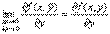
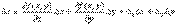
Определение. Выражение называется полным приращениемфункции f(x, y) в некоторой точке (х, у), где a₁ и a₂ – бесконечно малые функции при Dх ® 0 и Dу ® 0 соответственно.

Определение: Полным дифференциаломфункции z = f(x, y) называется главная линейная относительно Dх и Dу приращения функции Dz в точке (х, у).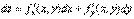

Для функции произвольного числа переменных:

Пример. Найти полный дифференциал функции