Миноры и алгебраические дополнения. Теорема Лапласа

Минором Мij квадратной матрицы n-го порядка для элемента аij называется определитель (n-1)-ого порядка, полученный с данного вычёркиванием i-ой строки и j-ого столбца.

Алгебраическое дополнение элемента 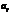определителя 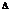определитель

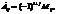где 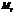- минор

элемента .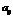

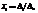
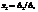
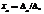
Теорема Лапласа. В данной квадратной матрице А(n x n ) вычеркнем k строк (1£k£n). Тогда равно сумме произведений всевозможных миновров к-того порядка из данных строк на их алгебраические дополнения: 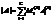. То же для столбцов. Теорема удобна для матриц с большим кол-вом нулей.

Обратная матрица. Необходимое и достаточное условия существования обратной матрицы

Определим операцию деления матриц как операцию, обратную умножению.Опр.Если существуют квадратные матрицы Х и А одного порядка, удовлетворяющие условию:

XA = AX = E,где Е - единичная матрица того же самого порядка, что и матрица А, то матрица Х называется обратнойк матрице А и обозначается А^-1.Каждая квадратная матрица с определителем, не равным нулю имеет обратную матрицу и притом только одну. Рассмотрим общий подход к нахождению обратной матрицы.Исходя из определения произведения матриц, можно записать:AX = E Þ 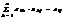, i=(1,n), j=(1,n), e_ij = 0, i ¹ j,

e_ij = 1, i = j .Таким образом, получаем систему уравнений: 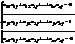Решив эту систему, находим элементы матрицы Х.

9 Ранг матрицы. Теорема об инвариантности ранга матрицы.

Ранг матрицы

Рангом матрицы А наз наивысший из порядков миноров этой матрицы не равных нулю.А=(аij)=(a11 a12 … a1n; a21 a22 … a2n; …; am1 am2 … amn) m*x Возьмем и выделим какой-нибудь минор порядка А (а11 а12; а21 а22). Если этот минор не равен нулю то его строки(столбцы) линейно независимы, тогда первые 2-е строки этой матрицы линейно независ. Ранг матрицы А будет не меньше 2-х. При нахождении ранга матрицы пользуются методом окомляющих миноров. Этот метод состоит в том что минор второго порядка окомляют одной строкой и одним столбцом, т.е строят минор 3-го порядка. Если же миноры 3-его порядка окомляющие данный минор 2-го порядка равны нулю, то матрица А не содержит миноров порядка большего 2-х, не равных нулю и ее ранг равен 2-м.Если же есть хотя бы один минор 3-го порядка который не равен нулю, то ранг матрицы не менее 3-х и процедуру окомления 3-порядка продолжают, в итоге будет найден минор 4-го порядка не равный нулю. Для которого все окомляющие миноры n+1-го порядка равны нулю. Тогда ранг матрицы А равен n. Разность матрицы обозн. R(A). Замечания: 1)Ранг нулевой матрицы равен нулю; 2)ранг матрицы равен max числу его линейно независимых строк.

Теорема (об инвариантности ранга при элементарных преобразованиях): Введём обозначение А~В для матриц, полученных друг из друга элементарными преобразованиями. Тогда справедливо утверждение: Если А~В, то их ранги равны.

Невырожденные системы.Фор-ы Краме. Метод Гаусса.