Несобственные интегралы первого рода

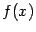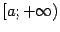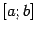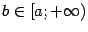Определение 4.1 Предположим, что функция задана на бесконечном промежутке вида и интегрируема на любом конечном отрезке , где . Таким образом, мы можем рассмотреть функцию

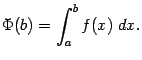
Если эта функция имеет предел 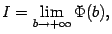то число 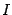называется значением несобственного интеграла первого рода

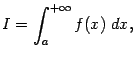
а сам интеграл 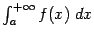называется сходящимся (иными словами, интеграл 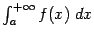сходится).

Если же предела 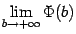не существует (например, есл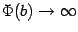и при 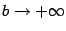), то интеграл 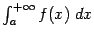называется расходящимся (то есть расходится) и не имеет никакого числового значения.

Геометрически, в случае 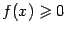, величина несобственного интеграла 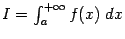означает, по определению, площадь бесконечно длинной области 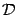, лежащей в координатной плоскости между лучом 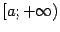на оси 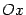, графиком 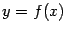и вертикальным отрезком 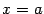(см. рис.).

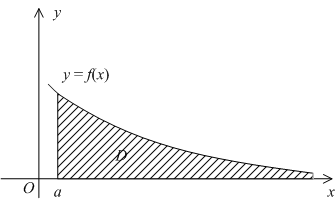
Рис.4.1.

Сходящиеся интегралы соответствуют таким областям 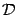, площадь которых конечна (хотя сама область 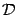неограничена), а расходящиеся (в случае 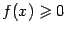) -- неограниченным областям с бесконечной площадью. В случае, когда 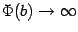при 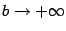, часто пишут формально:

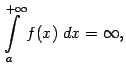
однако нужно ясно понимать, что эта запись означает расходимость интеграла и отсутствие у него числового значения.

Само определение значения интеграла через предел интегралов по конечным, но увеличивающимся отрезкам означает исчерпание площади 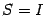путем учёта все большей её части 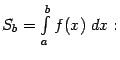правый вертикальный отрезок, проведённый при 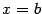, отодвигается всё дальше и дальше в бесконечность; в пределе будет учтена вся площадь под графиком 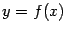(см. рис.).

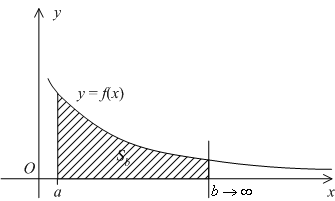
Рис.4.2

Глава 3. Признаки сходимости и расходимости несобственных интегралов

Теорема 1. Пусть фиксировано число и функция интегрируема на любом отрезке , где . Тогда если несобственный интеграл сходится, то при любом сходится интеграл . Обратно, если при некотором сходится интеграл , то сходится и интеграл .

Теорема 2 (теоpема сpавнения) Пусть даны две функции и , заданные на , причём при всех выполняется неравенство

Тогда из сходимости интеграла от большей функции, , следует сходимость интеграла от меньшей функции, , причём а из расходимости интеграла от меньшей функции, , следует расходимость интеграла от большей функции, :

Геометрически доказанное утверждение почти очевидно: оно означает, что если площадь под верхним графиком на следующем рисунке (она заштрихована), конечна, то конечна и имеет меньшее значение площадь под нижним графиком (она имеет двойную штриховку).

Рис. 5.

Если условие неотрицательности функций и не предполагается, то оба утверждения теоремы могут оказаться не верны: так, если взять и при всех , то интеграл от большей функции, оказывается сходящимся (его значение, очевидно, равно 0), а интеграл от меньшей функции, -- расходится (докажите расходимость, вычислив интеграл и рассмотрев его поведение при ).

При помощи теоремы 2 можем в некоторых случаях исследовать сходимость интеграла, не вычисляя его значения. Для доказательства сходимости интеграла от функции достаточно найти более простую функцию , для которой интеграл легко вычисляется и сходится. Согласно теореме, тогда исходный интеграл тоже сходится, причём мы получаем оценку его величины: . Если же нам нужно доказать расходимость интеграла , то достаточно найти такую (более просто устроенную) функцию , что и интеграл расходится.

Признак сходимости Абеля:

1. пусть функции f(x) и g(x) определены в промежутке , причём f(x) интегрируема в этом промежутке, т.е. интеграл сходится (условно или абсолютно);

2. g(x) монотонна и ограничена: .

Тогда интеграл сходится.

Признак сходимости Дирихле:

1. пусть функция f(x) интегрируема в любом конечном промежутке [a, b], и интеграл по этому промежутку ограничен (как функция верхнего предела b): ;