Нахождение наименьшего и наибольшего значения функции на заданном промежутке
Если функция 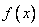 определена и непрерывна в замкнутом промежутке
определена и непрерывна в замкнутом промежутке 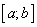 , то она достигает в этом промежутке своих наибольшего и наименьшего значений.
, то она достигает в этом промежутке своих наибольшего и наименьшего значений.
Алгоритм решения задачи 2.
1) Найти производную функции 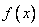 .
.
2) Найти стационарные точки (и точки, подозрительные на экстремум), решив уравнение 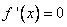 . Обратить внимание на точки, в которых не существует двусторонней конечной производной.
. Обратить внимание на точки, в которых не существует двусторонней конечной производной.
3) Вычислить значения функции в стационарных точках и на границах интервала.
4) Выбрать из полученных значений наибольшее (наименьшее).
Правило раскрытия неопределенности Лопиталя-Бернулли
Теорема Лопиталя (также правило Бернулли — Лопиталя) — метод нахождения пределов функций, раскрывающий неопределённости вида 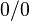 и
и 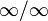 . Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
. Обосновывающая метод теорема утверждает, что при некоторых условиях предел отношения функций равен пределу отношения их производных.
Теорема Лопиталя:
Если:
1. 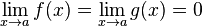 или
или 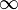 ;
;
2. 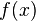 и
и 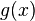 дифференцируемы в окрестности
дифференцируемы в окрестности 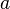 ;
;
3. 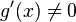 в окрестности
в окрестности 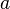 ;
;
4. существует 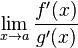 ,
,
то существует 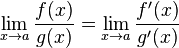 .
.
Пределы также могут быть односторонними.
Касательная к плоской кривой. Выпуклость и вогнутость плоской кривой
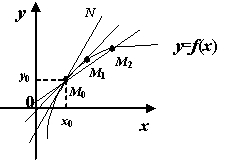
Касательной к линии 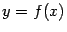 в точке
в точке 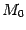 называется прямая
называется прямая 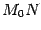 , служащая предельным положением секущих (прямых
, служащая предельным положением секущих (прямых 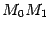 ), при условии, что точка
), при условии, что точка 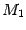 приближается, следуя по линии
приближается, следуя по линии 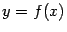 , к точке касания
, к точке касания 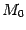 .
.
Уравнение касательной к графику 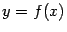 при
при 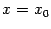 , то есть касательной, проходящей через точку
, то есть касательной, проходящей через точку 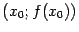 с угловым коэффициентом, равным производной
с угловым коэффициентом, равным производной 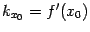 функции
функции 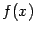 в точке
в точке 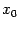 :
:
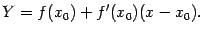
Выпуклость и вогнутость плоской кривой
Теорема 1. Если во всех точках интервала (a, b) вторая производная функции f (x) отрицательна, т.е. 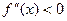 , то кривая y = f (x) на этом интервале обращена выпуклостью вверх (кривая выпукла).
, то кривая y = f (x) на этом интервале обращена выпуклостью вверх (кривая выпукла).
Теорема 1′. Если во всех точках интервала (b, с) вторая производная функции
f (x) положительна, т.е. 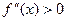 , то кривая y = f (x) на этом интервале обращена выпуклостью вниз (кривая вогнута).
, то кривая y = f (x) на этом интервале обращена выпуклостью вниз (кривая вогнута).
Точки перегиба графика функции. И нахождение.
Определение. Точка, отделяющая выпуклую часть кривой от вогнутой, называется точкой перегиба кривой.
Очевидно, что в точке перегиба касательная пересекает кривую.
Теорема 2. Пусть кривая определяется уравнением 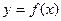 . Если вторая производная f’’ (a) = 0 или f’’ (a) не существует и при переходе через точку х = а производная f’’(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.
. Если вторая производная f’’ (a) = 0 или f’’ (a) не существует и при переходе через точку х = а производная f’’(x) меняет знак, то точка кривой с абсциссой х = а является точкой перегиба.
Асимптоты
Асимптота — прямая, обладающая тем свойством, что расстояние от точки кривой до этой прямой стремится к нулю при удалении точки вдоль ветви в бесконечность.
Вертикальная асимптота — прямая вида 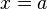 при условии существования предела
при условии существования предела 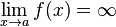 .
.
Как правило, при определении вертикальной асимптоты ищут не один предел, а два односторонних (левый и правый). Это делается с целью определить, как функция ведёт себя по мере приближения к вертикальной асимптоте с разных сторон. Например:
1. 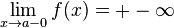
2. 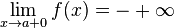
Замечание: обратите внимание на знаки бесконечностей в этих равенствах.
Горизонтальная асимптота — прямая вида 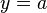 при условии существования предела
при условии существования предела
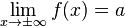 .
.
Наклонная
Наклонная асимптота — прямая вида 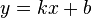 при условии существования пределов
при условии существования пределов
Пример наклонной асимптоты
1. 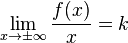
2. 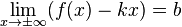
Замечание: функция может иметь не более двух наклонных (горизонтальных) асимптот.
Замечание: если хотя бы один из двух упомянутых выше пределов не существует (или равен 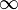 ), то наклонной асимптоты при
), то наклонной асимптоты при 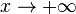 (или
(или 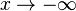 ) не существует.
) не существует.
Порядок нахождения асимптот
1. Нахождение вертикальных асимптот.
2. Нахождение двух пределов 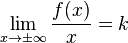
3. Нахождение двух пределов 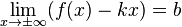 :
:
если 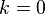 в п. 2.), то
в п. 2.), то 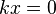 , и предел
, и предел 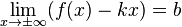 находится по формуле горизонтальной асимптоты,
находится по формуле горизонтальной асимптоты, 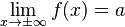 .
.
