Дифференциальное уравнение с разделяющимися переменными и его решение.

Дифференциальное уравнение первого порядка y' = f(x,y) называется уравнением с разделяющимися переменными, если функцию f(x,y) можно представить в виде произведения двух функций, зависящих только от x и y:

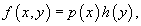
где p(x) и h(y) − непрерывные функции.

ассматривая производную y' как отношение дифференциалов 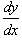, перенесем dx в правую часть и разделим уравнение на h(y):

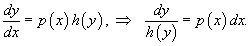
Разумеется, нужно убедиться, что h(y) ≠ 0. Если найдется число x₀, при котором h(x₀) = 0, то это число будет также являться решением дифференциального уравнения. Деление на h(y) приводит к потере указанного решения.

Обозначив 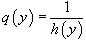, запишем уравнение в форме:

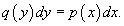
Теперь переменные разделены и мы можем проинтегрировать дифференциальное уравнение:

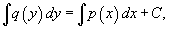
где C − постоянная интегрирования.

Вычисляя интегралы, получаем выражение

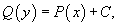
описывающее общее решение уравнения с разделяющимися переменными.

Линейные однородные уравнения второго порядка с постоянными коэффициентами.

Рассмотрим линейное дифференциальное уравнение вида

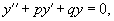
где p, q − постоянные коэффициенты.
Для каждого такого дифференциального уравнения можно записать так называемое характеристическое уравнение:

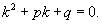
Обшее решение однородного дифференциального уравнения зависит от корней характеристического уравнения, которое в данном случае будет являться квадратным уравнением. Возможны следующие случаи:

1. Дискриминант характеристического квадратного уравнения положителен: D > 0. Тогда корни характеристического уравнения k₁ и k₂ действительны и различны. В этом случае общее решение описывается функцией

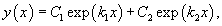где C₁ и C₂ − произвольные действительные числа.

1. Дискриминант характеристического квадратного уравнения равен нулю: D = 0. Тогда корни действительны и равны. В этом случае говорят, что существует один корень k₁ второго порядка. Общее решение однородного дифференциального уравнения имеет вид:

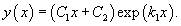
1. Дискриминант характеристического квадратного уравнения отрицателен: D < 0. Такое уравнение имеет комплексно-сопряженные корни k₁ = α + βi, k₁ = α − βi. Общее решение записывается в виде

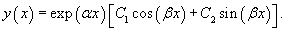
Рассмотренные три случая удобно представить в виде таблицы:

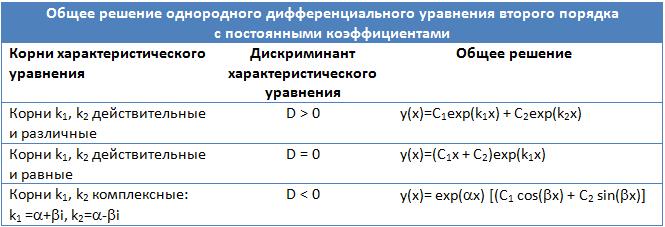Элемент комбинаторики: размещения, перестановки, сочетания, сво-во сочетания.

Размещения: из «n» элементов по «m» в каждом из которых по «m» элементов и отличаются такие соединения друг от друга самими элементами и их порядком.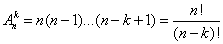

Перестановка: называется из «n» элементов называются такие соединения в каждом из которых по «n» элементов и отличаются они друг от друга только порядком самих элементов.

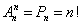
Сочетания: из «n» элементов по «m» называются такие соединения в каждом из которых по «m» элементов и отличаются они друг от друга только самими элементами.

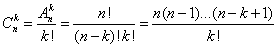
Свойства сочетаний:

1.

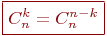
2.

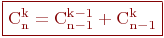
3.

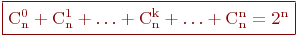
4.

5.

Виды событий. Примеры.

Достоверным событием называют событие которое обязательно произойдет в результате данного испытания ( восход солнца).

Событие которое никогда не произойдет при данном испытании называется невозможным.

Случайными событиями будут называться события которые могут произойти , а могут и не произойти при данном испытании

Совместными называются события если появление одного из них не исключает появление другого.

Два события называются несовместными если появление одного из них исключает появление другого.

Полной группой случайных событий называются события состоящие в появлении хотя бы одного из этих событий.

Два события называют противоположными если они не совместимы и образуют полную группу.

Равновозможными называются события если они имеют одинаковые шансы их появления.

Благоприятствующими исходами испытания называются исходы испытания при которых появляется случайное событие А.