Основные теоремы о дифференцируемых функциях: теоремы Ферма, Ролля, Лагранжа, Коши, правило Лопиталя.
Теорема Ферма. Пусть функция имеет на множестве точку экстремума , причём множество содержит некоторую -окрестность точки . Тогда либо имеет в точке производную, равную 0, то есть , либо производная в точке не существует. Замечание. Заметим, что условие означает, что тангенс угла наклона касательной к графику , проведённой при , равен 0. Отсюда , то есть теорема Ферма утверждает, что касательная, проведённая в точке экстремума, горизонтальна (если эта касательная существует).
Теорема Ролля. Пусть функция дифференцируема на интервале , непрерывна в точках и и принимает в этих точках значение 0: . Тогда найдётся хотя бы одна точка , в которой .Замечание . Это утверждение можно переформулировать так: между двумя корнями и дифференцируемой функции обязательно найдётся корень её производной . Условие означает, что касательная, проведённая к графику при , расположена горизонтально.
Заметим также, что теорема Ролля не утверждает, что корень -- единственный корень производной на интервале ; на этом интервале может находиться несколько корней производной.
Теорема Лангранжа.Пусть функция дифференцируема на интервале и непрерывна в точках и . Тогда найдётся такая точка , что 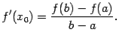 (1). Замечание. Формулу (1) можно записать в виде
(1). Замечание. Формулу (1) можно записать в виде 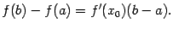 (2). Если считать, что аргументу а придано приращение
(2). Если считать, что аргументу а придано приращение 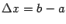 , то функция получает приращение
, то функция получает приращение 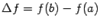 . (При этом мы не считаем, что
. (При этом мы не считаем, что 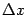 и
и 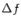 стремятся к 0, то есть это конечные, а не бесконечно малые, приращения.) При этих обозначениях формулу (2) мы можем записать в виде
стремятся к 0, то есть это конечные, а не бесконечно малые, приращения.) При этих обозначениях формулу (2) мы можем записать в виде 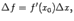 , в котором участвуют конечные приращения аргумента и функции. Поэтому формулу (2) называют формулой конечных приращений.
, в котором участвуют конечные приращения аргумента и функции. Поэтому формулу (2) называют формулой конечных приращений.
Теорема Коши.Пусть функции 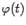 и
и 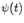 дифференцируемы на интервале
дифференцируемы на интервале 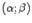 и непрерывны при
и непрерывны при 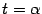 и
и 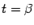 , причём
, причём 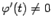 при всех
при всех 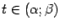 . Тогда в интервале
. Тогда в интервале 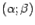 найдётся такая точка
найдётся такая точка 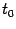 , что
, что 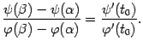 Замечание.Можно считать функции и координатами движущейся на плоскости точки, которая описывает линию , соединяющую начальную точку с конечной точкой . (Тогда уравнения и параметрически задают некоторую зависимость , графиком которой служит линия) .
Замечание.Можно считать функции и координатами движущейся на плоскости точки, которая описывает линию , соединяющую начальную точку с конечной точкой . (Тогда уравнения и параметрически задают некоторую зависимость , графиком которой служит линия) .  Отношение
Отношение 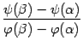 , как нетрудно видеть из чертежа, задаёт тогда угловой коэффициент хорды, соединяющей точки
, как нетрудно видеть из чертежа, задаёт тогда угловой коэффициент хорды, соединяющей точки 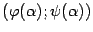 и
и 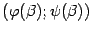 . В то же время, по формуле производной функции, заданной параметрически, имеем:
. В то же время, по формуле производной функции, заданной параметрически, имеем: 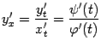 . Значит, дробь
. Значит, дробь 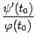 -- это угловой коэффициент касательной к линии L в некоторой точке
-- это угловой коэффициент касательной к линии L в некоторой точке 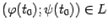 . Тем самым утверждение теоремы означает, с геометрической точки зрения, что на линии L найдётся точка, такая что проведённая в этой точке касательная параллельна хорде, соединяющей крайние точки линии. Но это -- то же самое утверждение, которое составляло геометрический смысл теоремы Лагранжа. Только в теореме Лагранжа линия L была задана явной зависимостью
. Тем самым утверждение теоремы означает, с геометрической точки зрения, что на линии L найдётся точка, такая что проведённая в этой точке касательная параллельна хорде, соединяющей крайние точки линии. Но это -- то же самое утверждение, которое составляло геометрический смысл теоремы Лагранжа. Только в теореме Лагранжа линия L была задана явной зависимостью 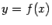 , а в теореме Коши -- зависимостью, заданной в параметрической форме.
, а в теореме Коши -- зависимостью, заданной в параметрической форме.
Правило Лопиталя.представляет собой метод вычисления пределов, имеющих неопределенность типа 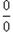 или
или 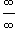 . Пусть a является некоторым конечным действительным числом или равно бесконечности.
. Пусть a является некоторым конечным действительным числом или равно бесконечности.
Если 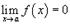 и
и 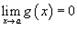 , то
, то 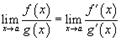 ; Если
; Если 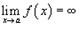 и
и 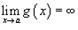 , то
, то 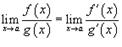 аналогично.
аналогично.
