Теоремы Ферма и Ролля
Теорема Ролля.Если функция 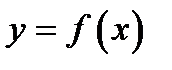 непрерывна в замкнутом интервале
непрерывна в замкнутом интервале 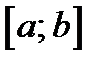 , дифференцируема во всех внутренних точках этого интервала и, кроме того, на концах интервала принимает одинаковые значения, то в этом интервале найдётся хотя бы одна точка
, дифференцируема во всех внутренних точках этого интервала и, кроме того, на концах интервала принимает одинаковые значения, то в этом интервале найдётся хотя бы одна точка 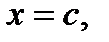
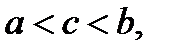 в которой значение производной
в которой значение производной 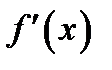 обращается в нуль.
обращается в нуль.
 Доказательство.Если функция
Доказательство.Если функция 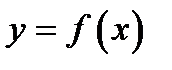 не изменяется, т. е. остаётся постоянной (
не изменяется, т. е. остаётся постоянной ( 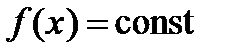 ), то
), то 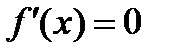 и теорема для этого случая доказана. Пусть теперь функция
и теорема для этого случая доказана. Пусть теперь функция 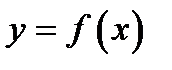 с изменением
с изменением  изменяется. Пусть, например, начиная от точки
изменяется. Пусть, например, начиная от точки 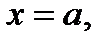 с увеличением
с увеличением 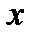 значение
значение 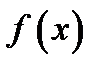 увеличивается, как показано на рис. 60. Тогда значение
увеличивается, как показано на рис. 60. Тогда значение 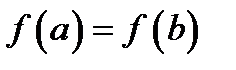 функции
функции 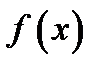 не является наибольшим ее значением на
не является наибольшим ее значением на 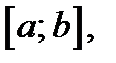 следова-тельно, потеореме 1 своё наибольшее значение функция
следова-тельно, потеореме 1 своё наибольшее значение функция 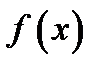 примет в некоторой точке
примет в некоторой точке 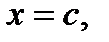 лежащей внутри интервала
лежащей внутри интервала 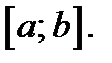 Следовательно, значение
Следовательно, значение 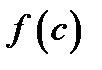 будет наибольшим значением функции
будет наибольшим значением функции 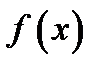 в интервале
в интервале 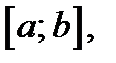 т. е.
т. е. 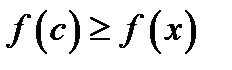 для всех
для всех 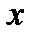 из
из 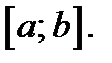
Теорема Ролля будет доказана, если мы покажем, что в точке 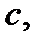 в которой функция
в которой функция 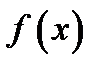 принимает наибольшее значение
принимает наибольшее значение 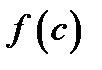 в интервале
в интервале 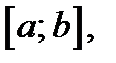 производная
производная 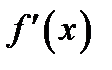 обращается в нуль. Таким образом, доказательство свелось к доказательству следующего утверждения.
обращается в нуль. Таким образом, доказательство свелось к доказательству следующего утверждения.
Теорема Ферма.Если дифференцируемая в интервале 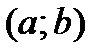 функ-ция
функ-ция 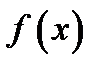 принимает в точке
принимает в точке 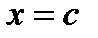 (
( 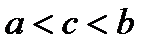 ) своё наибольшее значение в
) своё наибольшее значение в 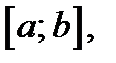 то в этой точке производная
то в этой точке производная 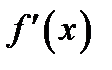 обращается в нуль, т. е.
обращается в нуль, т. е. 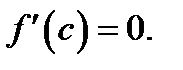
Доказательство. Возьмём точку 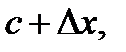 лежащую достаточно близко к точке
лежащую достаточно близко к точке 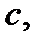 считая, что
считая, что 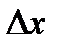 – величина малая. Эта точка лежит правее
– величина малая. Эта точка лежит правее  при
при 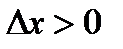 и левее при
и левее при 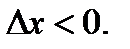 Так как
Так как 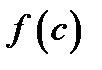 есть наибольшее значение функции
есть наибольшее значение функции 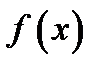 в интервале
в интервале 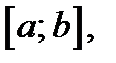 то ясно, что
то ясно, что 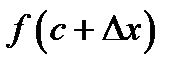
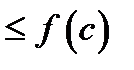 как для
как для 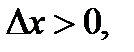 так и для
так и для 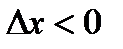 , что можно переписать в виде
, что можно переписать в виде 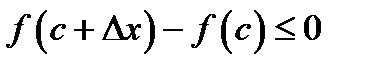 для всех
для всех 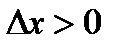 и
и 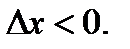 Это неравенство умножим на число
Это неравенство умножим на число 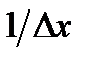 , положительное при
, положительное при 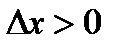 и отрицательное при
и отрицательное при 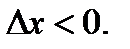 При этом знак неравенства не изменится при
При этом знак неравенства не изменится при 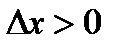 и изменится на обратный при
и изменится на обратный при 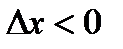 . В результате получим
. В результате получим
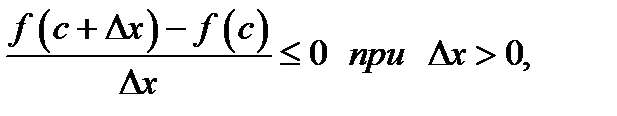
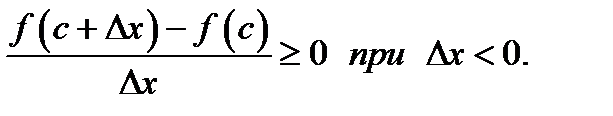
В этих неравенствах перейдём к пределу при 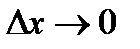 и согласно теории пределов (теорема 15 главы 4) будем иметь
и согласно теории пределов (теорема 15 главы 4) будем иметь
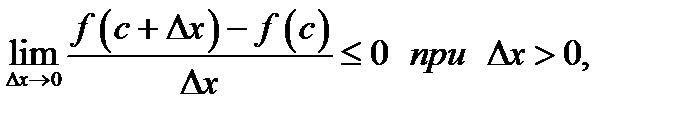
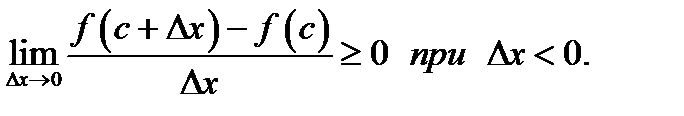
По условию теоремы функция 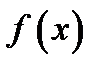 дифференцируема во всех внутренних точках интервала
дифференцируема во всех внутренних точках интервала 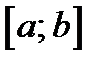 и в точке
и в точке 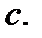 Это значит, что существует производная
Это значит, что существует производная 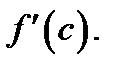 Но производная равна пределу, входящему в предыдущие неравенства. Этот предел является обычным двусторонним и существует независимо от знака
Но производная равна пределу, входящему в предыдущие неравенства. Этот предел является обычным двусторонним и существует независимо от знака 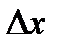 . Следовательно, в двух предыдущих неравенствах пределы одинаковы и равны
. Следовательно, в двух предыдущих неравенствах пределы одинаковы и равны 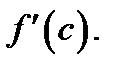 Поэтому предыдущие неравенства можно переписать так:
Поэтому предыдущие неравенства можно переписать так: 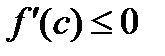 при
при 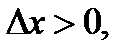
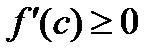 при
при 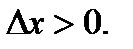 Неравенства должны выполняться одновременно, а это возможно, если
Неравенства должны выполняться одновременно, а это возможно, если 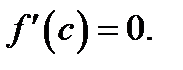 Теорема Ферма доказана, а вместе с ней доказана теорема Ролля.
Теорема Ферма доказана, а вместе с ней доказана теорема Ролля.
Условие 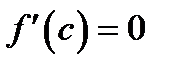 геометрически означает, что касательная к кривой
геометрически означает, что касательная к кривой 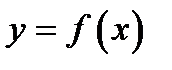 в её точке с абсциссой
в её точке с абсциссой  параллельна оси
параллельна оси 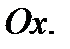 В самом деле, вычисляемая в точке
В самом деле, вычисляемая в точке  производная
производная 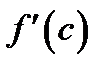 равна тангенсу угла
равна тангенсу угла 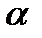 наклона к оси абсцисс касательной к кривой
наклона к оси абсцисс касательной к кривой 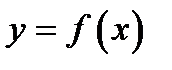 в её точке с абсциссой
в её точке с абсциссой 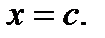 Если эта производная равна нулю, то
Если эта производная равна нулю, то 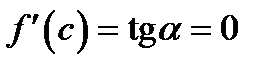 и
и 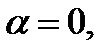 т. е. касательная параллельна оси
т. е. касательная параллельна оси 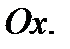
30. Теоремы Коши и Лагранжа
Теорема Коши. Если функции 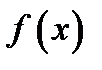 и
и 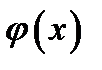 непрерывны в замкнутом интервале
непрерывны в замкнутом интервале 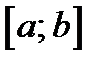 и дифференцируемы во всех внутренних точках этого интервала, причём всюду в этом интервале
и дифференцируемы во всех внутренних точках этого интервала, причём всюду в этом интервале 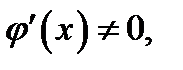 то в
то в 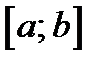 найдется хотя бы одна точка
найдется хотя бы одна точка 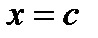 (
( 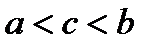 ), для которой справедлива формула
), для которой справедлива формула
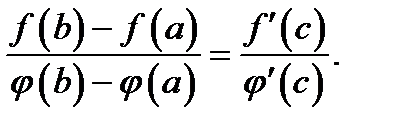 (3)
(3)
Доказательство.Возьмём функцию
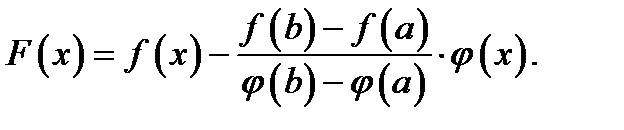 (4)
(4)
Она удовлетворяет следующим условиям:
· непрерывна на 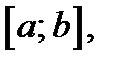 действительно,
действительно, 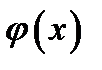 непрерывна в этом интервале по условию, поэтому произведение дроби и
непрерывна в этом интервале по условию, поэтому произведение дроби и 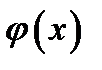 также есть непрерывная функция на этом интервале согласно теореме о произведении непрерывных функций;
также есть непрерывная функция на этом интервале согласно теореме о произведении непрерывных функций;
· разность, стоящая в правой части (4), – непрерывная функция согласно теореме о разности непрерывных функций;
· 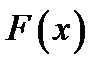 дифференцируема во всех внутренних точках интервала
дифференцируема во всех внутренних точках интервала 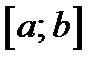 и имеет производную
и имеет производную
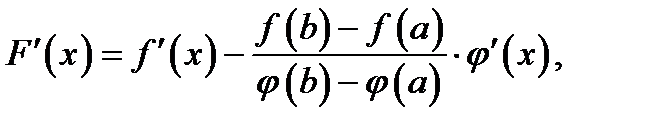 (5)
(5)
где производные 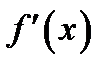 и
и 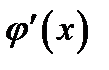 существуют согласно условию теоремы;
существуют согласно условию теоремы;
· значения функции 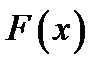 на концах
на концах 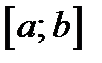 равны, т. е.
равны, т. е. 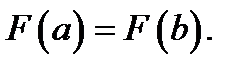 Чтобы непосредственно убедиться в этом, надо подставить в (4) сначала
Чтобы непосредственно убедиться в этом, надо подставить в (4) сначала 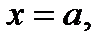 затем
затем 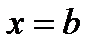 и сравнить выражения.
и сравнить выражения.
Таким образом, функция 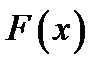 удовлетворяет всем условиям теоремы Ролля, согласно которой на интервале
удовлетворяет всем условиям теоремы Ролля, согласно которой на интервале 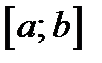 найдется хотя бы одна точка
найдется хотя бы одна точка 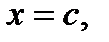
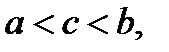 в которой
в которой 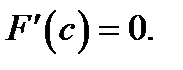 Это значит, что выражение (5) при
Это значит, что выражение (5) при 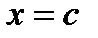 обращается в нуль, т. е.
обращается в нуль, т. е.
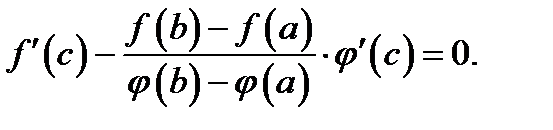
Учтя, что 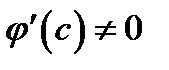 по условию теоремы, и поделив последнее соотношение на
по условию теоремы, и поделив последнее соотношение на 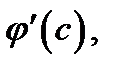 придём к формуле (3).
придём к формуле (3).
Теорема Лагранжа. Если функция 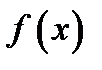 непрерывна в замкнутом интервале
непрерывна в замкнутом интервале 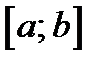 и дифференцируема во всех внутренних точках этого интервала, то в
и дифференцируема во всех внутренних точках этого интервала, то в 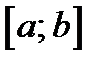 найдется хотя бы одна точка
найдется хотя бы одна точка 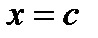 (
( 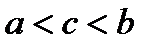 ), для которой справедлива формула
), для которой справедлива формула
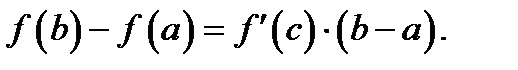 (6)
(6)
Доказательство.Кроме функции 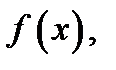 указанной в теореме, возьмём ещё одну функцию
указанной в теореме, возьмём ещё одну функцию 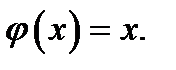 Она дифференцируема всюду в интервале
Она дифференцируема всюду в интервале 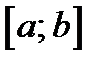 , так как имеет производную
, так как имеет производную 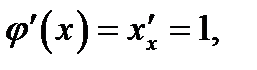 причём
причём 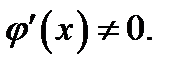 Кроме того,
Кроме того, 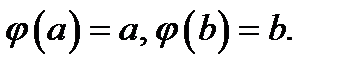 Таким образом, эта функция
Таким образом, эта функция 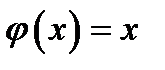 вместе с функцией
вместе с функцией 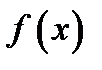 удовлетворяют всем условиям теоремы Коши. Запишем формулу (3) для этих функций:
удовлетворяют всем условиям теоремы Коши. Запишем формулу (3) для этих функций: 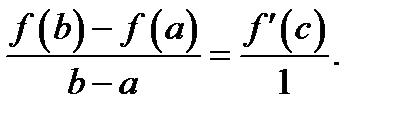 Здесь
Здесь 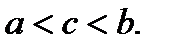 Умножив это соотношение на
Умножив это соотношение на 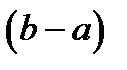 , получим (6). Теорема доказана.
, получим (6). Теорема доказана.
31. Правило Лопиталя
Теорема.Пусть функции 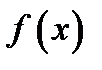 и
и 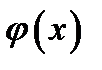 одновременно стремятся к нулю или к бесконечности при
одновременно стремятся к нулю или к бесконечности при 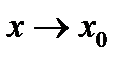 (
( 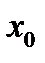 – заданное число) или при
– заданное число) или при 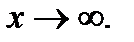 Если при этом отношение производных
Если при этом отношение производных 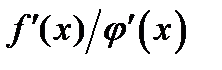 имеет предел, то отношение функций также имеет предел, равный пределу отношения производных, т. е.
имеет предел, то отношение функций также имеет предел, равный пределу отношения производных, т. е.
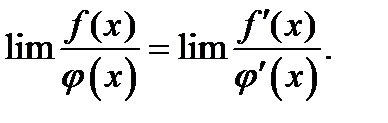 (7)
(7)
Доказательство. Докажем теорему для случая, когда при 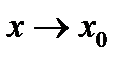 обе функции имеют пределы, равные нулю, и непрерывны в точке
обе функции имеют пределы, равные нулю, и непрерывны в точке 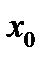 , т. е.
, т. е. 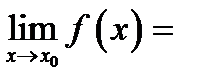
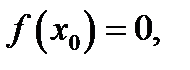
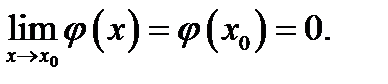 В теореме говорится о пределе отношения производных
В теореме говорится о пределе отношения производных 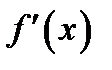 и
и 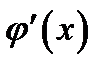 при
при 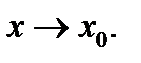 Это означает, что указанные производные мы предполагаем существующими всюду вблизи
Это означает, что указанные производные мы предполагаем существующими всюду вблизи 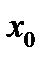 как слева, так и справа.
как слева, так и справа.
Возьмём интервал 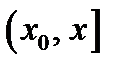 , считая, что
, считая, что 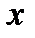 – некоторое фиксированное значение, достаточно близкое к
– некоторое фиксированное значение, достаточно близкое к 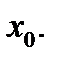 Тогда в этом интервале, включая
Тогда в этом интервале, включая 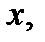 всюду существуют производные
всюду существуют производные 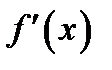 и
и 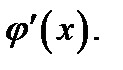 Следовательно, в интервале
Следовательно, в интервале 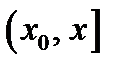 функции
функции 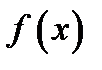 и
и 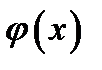 являются непрерывными, поскольку они дифференцируемы. Кроме того, функции
являются непрерывными, поскольку они дифференцируемы. Кроме того, функции 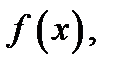
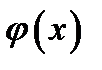 непрерывны и в точке
непрерывны и в точке 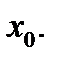 Таким образом, функции
Таким образом, функции 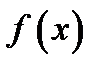 и
и 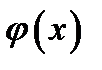 непрерывны в замкнутом интервале
непрерывны в замкнутом интервале 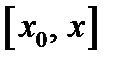 и дифференцируемы всюду внутри него. Дополнительно предположим, что
и дифференцируемы всюду внутри него. Дополнительно предположим, что 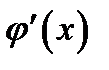 нигде в этом интервале не обращается в нуль (это предположение является естественным, т. к.
нигде в этом интервале не обращается в нуль (это предположение является естественным, т. к. 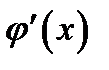 в формуле (7) стоит в знаменателе). Таким образом, эти две функции удовлетворяют всем условиям теоремы Коши. Поэтому для них и интервала
в формуле (7) стоит в знаменателе). Таким образом, эти две функции удовлетворяют всем условиям теоремы Коши. Поэтому для них и интервала 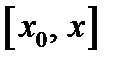 справедлива указанная теорема, когда в ней
справедлива указанная теорема, когда в ней 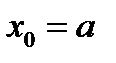 и
и 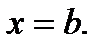 Итак,
Итак,
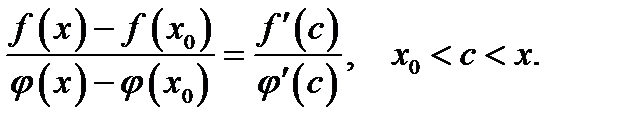
Но 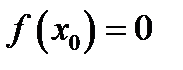 и
и 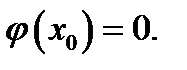 Следовательно, эта формула примет вид
Следовательно, эта формула примет вид
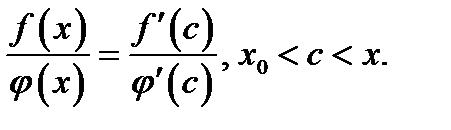 (8)
(8)
Согласно условию теоремы существует предел отношения производных 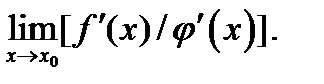 Отсюда согласно определению предела заключаем, что существует и предел
Отсюда согласно определению предела заключаем, что существует и предел 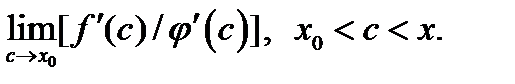 Этот предел будет равен предыдущему, и получим
Этот предел будет равен предыдущему, и получим
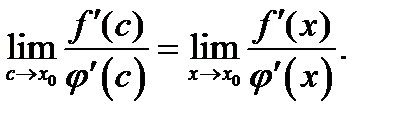 (9)
(9)
В соотношении (8) перейдём к пределу, когда 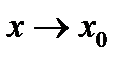 и
и 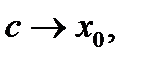 учитывая, что предел правой части существует. Тогда будет существовать и предел левой части, равный первому:
учитывая, что предел правой части существует. Тогда будет существовать и предел левой части, равный первому:
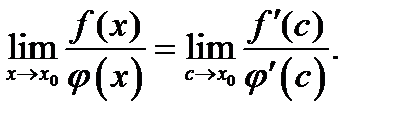 (10)
(10)
Сравнив формулы (9) и (10), придем к формуле (7). Теорема для указанного случая доказана. Случай, когда 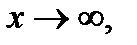 приводится к рассмотренному заменой
приводится к рассмотренному заменой 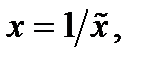 при этом
при этом 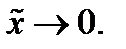 Доказательство, когда
Доказательство, когда 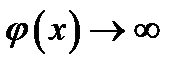 ,
, 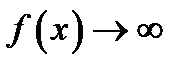 , опускаем.
, опускаем.
