Наибольшее и наименьшее значение функции, непрерывной на отрезке

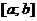Если функция определена и непрерывна на отрезке , то, согласно второй теореме Вейерштрасса, она на этом отрезке принимает наибольшее и наименьшее значения.

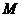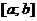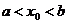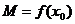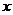Если свое наибольшее значение функция принимает во внутренней точке отрезка , т. е. когда , то будет локальным максимумом функции . В этом случае существует окрестность точки такая, что значения для всех точек из этой окрестности будут не больше 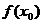как в точках слева от точки , так и в точках справа от точки .

Однако свое наибольшее значение 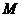функция может принимать и на концах отрезка .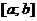

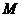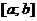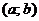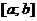Поэтому, чтобы найти наибольшее значение непрерывной на отрезке функции , надо найти все максимумы функции в интервале и значения на концах отрезка , т. е. 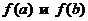, и выбрать среди них наибольшее число.

Наименьшим значением 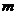непрерывной на отрезке 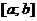функции будет наименьшее число среди всех минимумов функции в интервале 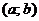и значений .

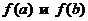Замечание 1. Если в промежутке 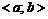, конечном или бесконечном, одна критическая точка и в ней максимум (минимум), то в ней наибольшее (наименьшее) значение.

Замечание 2. Если функция задана и непрерывна на некотором промежутке, не являющемся замкнутым, то среди значений функции на этом промежутке может не быть наибольшего и наименьшего.

Правило определения наибольших и наименьших значений функции на отрезке

1. Найти значения функции на концах отрезка: .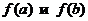

2. Определить критические точки первого рода.

3. Вычислить значение функции в критических точках первого рода (к.т.I): 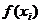, где .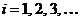

4. Выбрать из значений 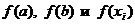наименьшее 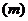и наибольшее 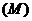значения функции.

Пример 18. Найти наибольшее и наименьшее значения функции 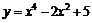на отрезке .

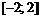▲ 1. Для вычисления функции в указанных точках используем схему Горнера:

.

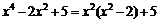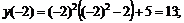так как данная функция четная, то .

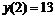2. Найдем производную: 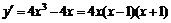. Она обращается в нуль в точках: 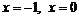, 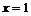. Все они лежат внутри отрезка .

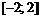3. Вычислим значения функции в к.т.I. Имеем: .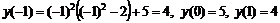

4. Имеем множество значений функции на концах отрезка и в к.т.I: 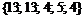. Значит, наименьшее значение равно 4, наибольшее значение равно 13.

Ответ: . ▼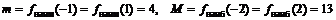

Пример 19. Найти наибольшее и наименьшее значения функции 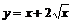на отрезке .

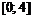▲ 1. .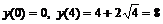

2. Найдем производную: 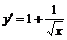. Производная в нуль не обращается 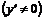. Производная не существует .

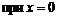3. К.т.I совпадает с левой границей данного отрезка.

4. Имеем множество значений функции на концах отрезка и в к.т.I: 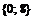. Значит, наименьшее значение равно 0, наибольшее значение равно 8.

Ответ: . ▼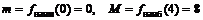

Пример 20. Найти наибольшее и наименьшее значения функции 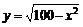на отрезке .

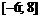▲ 1. .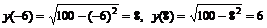

2. Найдем производную: 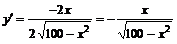. Производная обращается в нуль в точке 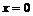. Производная не существует 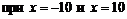, но обе эти точки не принадлежат данному отрезку.

3. Вычислим значения функции в к.т.I. Имеем: .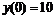

4. Имеем множество значений функции на концах отрезка и в к.т.I: 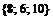. Значит, наименьшее значение равно 6, наибольшее значение равно 10.

Ответ: . ▼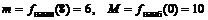

Пример 21. Найти наибольшее и наименьшее значения функции 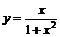на промежутке .

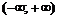2. Найдем производную: 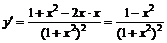. Она обращается в нуль в точках .

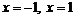3. Вычислим значения функции в к.т.I. Имеем: 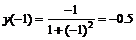. Так как данная функция нечетная, то .

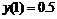4. Поскольку 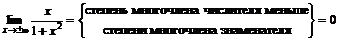, то наибольшее значение равно 0.5, наименьшее значение –0.5.

Ответ: . ▼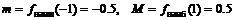

Пример 22. Найти наибольшее и наименьшее значения функции 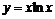на отрезке .

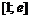▲ 1. .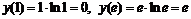

2. Найдем производную: 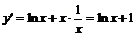. Она обращается в нуль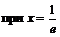

.

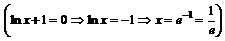Точка 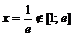, т. е. к.т.I нет.

4. Имеем множество значений функции на концах отрезка: 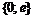. Значит, наименьшее значение равно 0, наибольшее значение равно .

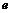Ответ: . ▼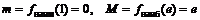

Пример 23. Найти наибольшее и наименьшее значения функции 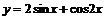на отрезке .

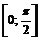▲ 1. .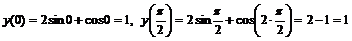

2. Найдем производную: 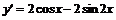. Если 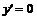, то

.

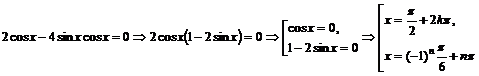
Из всех найденных критических точек только 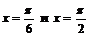принадлежат отрезку .

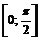3. Вычислим значения функции в к.т.I. Имеем: .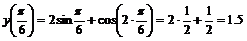

4. Имеем множество значений функции на концах отрезка и в к.т.I: 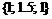. Значит, наименьшее значение равно 1, наибольшее значение равно 1.5.

Ответ: . ▼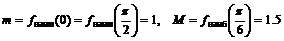

Знания и умения, которыми должен владеть студент