Разложение многочлена от n переменных в произведение не приводимых множителей

Рассматривая делимость в кольце многочленов от n переменных будем считать взятыми из поля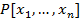

О1) Многочлен f ∈ 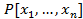делится на не нулевой многочлен g ∈ 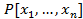если существует такой многочлен s∈ 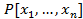, что f=gs, f⋮g

О2) Многочлен f ∈ 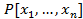называется не приводимым над P если ст f ≥1

f=gs, ст g=0 или ст s=0 и делятся на f.

О3) Многочлен f ∈ 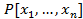называется приводимым или составным над полем P если ст f≥1 и существуют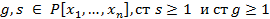

Отметим свойства не приводимых многочленов

1) Если f ∈ 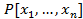не приводим над P то и всякий ассоциированный с ним многочлен также не приводим над P.

2) Если f g не приводимые над полем P и f⋮g то f и g ассоциированные.

3) Всякий многочлен f из кольца 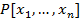степени 1 не приводим над P.

Указанные свойства аналогичны рассмотренных для многочленов от 1 переменной. Основной результат теории делимости заключается в возможности и единственности разложения многочленов на неприводимые множители, остается в силе и в кольце .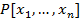

Т1: любой многочлен f ∈ 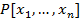ст f≥1 представим произведением не приводимых множителей и это представление единственно с точностью до нулевого члена.

Доказательство:

Доказательство будем вести методом математической индукции.

1) Если ст f=1 то f не приводим и разложение представимо всевали одним множителем с точность до постоянного множителя.

2) Пусть теорема верна для любого многочлена f такова что ст f≥1<m

3) Докажем истинность утверждения для любого многочлена ст f =m:

Если f не приводим над P то разложение будет представлено одним множителем, если f приводимый то существуют g,s ∈ 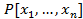такие, что f=gs, ст g≥1, ст s≥1 и учтем что, ст g<ст f, ст s<ст f è по предположению пункта 2 теоремы, для многочленов g и s, теорема верна. Таким образом мы f=gs - представление f в виде произведения не приводимых множителей.

Единственность такого разложения доказывается методом от противного.

Cсимметрические многочлены

Будим рассматривать многочлены над произвольной областью целостности.

О1 называется симметрическим если он не меняется при любой перестановке входящих в него переменных где –перестановка

Пример 1:

– симметрический

- не симметрический

Структура симметрических многочленов такова, что если сам симметрический многочлен содержит элемент , то он также должен содержать многочлен вида у которых выполнена замена иксов, а индексы образуют перестановку из номеров переменных x. Обозначим сумм различных одночленов, которые получаются из одночлена , . В частности каждый симметрический многочлен является суммой однородных многочленов

Особую роль среди симметрических многочленов играют элементарные симметрические многочлены.

По определению k-ый элементарный симметрический многочлен есть сумм всевозможных произведений по k различных переменных

Другую важную серию симметрических многочленов составляют степенные суммы:

Можно показать что, сумма разность и произведение симметрических многочленов также являются симметрическими

Пример 2:

–симметрические их произведение надо показать что он тоже симметрический

è - симметрический.

K из него можем выделить симметрические. Сами симметрический многочлен тоже образуют кольцо.

Рассмотрим ряд утверждений относительно симметрически многочленов.

Л1: Если лексико старший член симметрического многочлена то для последовательности степеней выполняется .

Доказательство:

Пусть u лексикографически старший член. Предположим . По условию f симметрический тогда по определению симметрического многочлена он в месте с одночленом U содержит одночлен . Исходя из предположения но по условию U старший то есть наше предположение привело к противоречию условию леммы следовательно наше предположение не верно.

Л2: Для любого одночлена где , a≠0 суш шествует многочлен лексикографически старшй член которого совподает c U.

Доказательство:

Лексикографически старший член многочлена является произведением старших членов элементарных симметричных многочленов с учетом их степеней:

Найденный лексикографически старший член должен быть равен одночлену U если

(2)

Решение системы (2) получаем в результате вычитания из i-го уравнения i+1 уравнение:

(3)

Такое решение единственно и учитывая что, , - целые не отрицательные числа а, следовательно могут быть показателями степеней. И так симметрический многочлен:

и лексикографически старший член ее совпадает с U(он единственен, что идет из единственности решения системы 2).

Доказанные леммы 1,2 позволяют рассмотреть основную теорему о симметрических многочленов.