Почленное интегрирование и дифференцирование рядов.

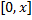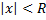7) Степенной ряд (1) в промежутке , где , всегда можно интегрировать почленно, так что:

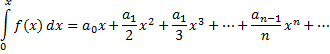
Значение 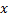здесь может совпадать и с одним из концов промежутка сходимости, если на этом конце ряд (1) сходится.

8) Степенной ряд (1) внутри его промежутка сходимости можно дифференцировать почленно, так что:

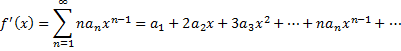
Утверждение сохраняет силу и для конца промежутка сходимости, если только написанный ряд на этом конце сходится.

Разложение элементарных функций в ряд Тейлора.

Ф., представляемая степенным рядом в его промежутке сходимости, имеет внутри этого промежутка производные всех порядков. Сам ряд, по отношению к этой ф., является не чем иным, как её рядом Тейлора.

Ф., которая разлагается в ряд Тейлора по степеням 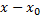, называется аналитической в т. .

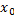Разложение элементарных функций.

1) Разложение в ряд функции .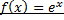

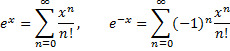
2) Разложение в ряды 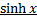и .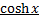

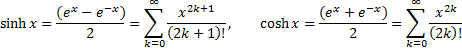
3) Разложение в ряды 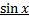и 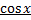. Формула Эйлера.

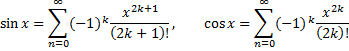
4) Разложение в ряд .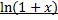

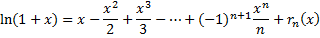
где

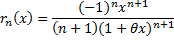
остаточный член в виде Лагранжа, где 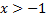и .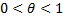

5) Разложение в степенной ряд степени бинома .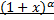

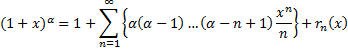
Если 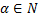, то ряд превращается в бином Ньютона.

6) Разложение в ряд .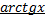

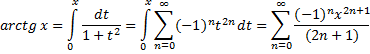
где .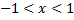

7) Разложение в ряд .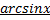

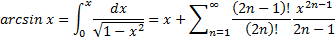
Тригонометрический ряд Фурье.

Теорема Дирихле. Разложение в ряд Фурье периодических, четных, нечетных и непериодических функций.

Тригонометрический ряд Фурье.

Если разлагается на отрезке 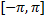в равномерно сходящийся тригонометрический ряд:

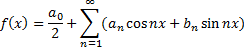
,то это разложение единственное и коэффициенты определяются по формулам:

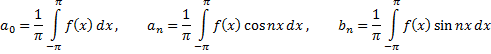
где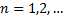

И называется: тригонометрический ряд Фурье, а 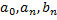– коэффициентами ряда Фурье.

Теорема Дирихле.

Опр1 (Кусочная монотонность).

Ф. называется кусочно монотонной на сегменте , если этот отрезок разбивается на конечное число сегментов: 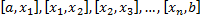, в каждом из которых ф. монотонна.

Если ф. кусочно монотонна на сегменте , то в любой внутренней т. этого сегмента 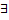правые и левые пределы её значений, т.е. пределы:

Т1. (Теорема Дирихле).

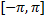Если ф. задана на сегменте и является на нем кусочно непрерывной, кусочно монотонной и ограниченной, то её тригонометрический ряд Фурье сходится во всех точках непрерывности этой функции:

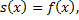
а во всех т. разрыва

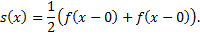
Разложение в ряд Фурье.

Разложение в ряд Фурье функций в интервале .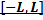

Пусть ф. кусочно-непрерывная и 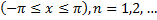, тогда ряд Фурье имеет вид:

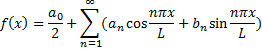
а коэффициенты Фурьеравны:

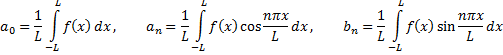
Разложение в ряд Фурье функций в интервале .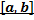

Если ф. определена в интервале , то её разложение в ряд определяется той же формулой:

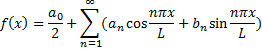
где 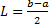, а коэффициенты Фурье равны:

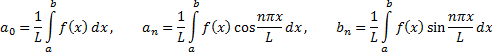
Разложение в ряд Фурье чётной функции.

Если ф. определена в интервале 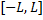, то её разложение в ряд определяется формулой:

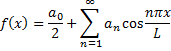
а коэффициенты Фурьеравны:

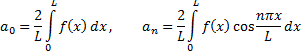
Разложение в ряд Фурье нечётной функции.

Если ф. определена в интервале 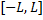, то её разложение в ряд определяется формулой:

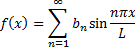
а коэффициенты Фурьеравны:

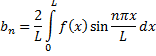
Комплексный анализ

Элементарные функции комплексного переменного.

Однозначные и многозначные функции. Обратные функции. Аналитические функции. Элементарные функции и их свойства