Интегрирование и дифференцирование степенных рядов
Определение. Функциональный ряд вида
,
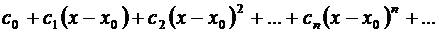где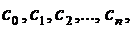 
… – действительные числа, называется степенным рядом.
Областью абсолютной сходимости ряда является интервал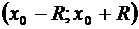 
, где число R – радиус сходимости.
Пусть степенной ряд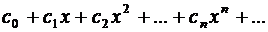 
имеет радиус сходимости R > 0. Тогда справедливы следующие положения:
1. Сумма ряда является непрерывной функцией от x во всем интервале сходимости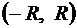 
.
2. Ряд равномерно сходится на любом отрезке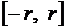 
, где 
.
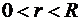3. Ряд можно почленно интегрировать по любому отрезку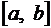 
, лежащему внутри интервала .
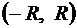4. Ряд можно почленно дифференцировать в любой точке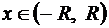 
сколь угодно раз.
Примечания:
1. При почленном интегрировании или дифференцировании степенного ряда получаются новые степенные ряды, при этом их радиус сходимости остается тот же.
2. Радиус сходимости степенного ряда можно найти по одной из формул:
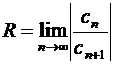, (10)
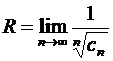(11)
при условии, что указанные пределы существуют,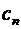 
– коэффициент ряда.
Задача 17.31[7]
Найти сумму ряда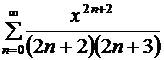 
.
Решение:
I способ. Найдем интервал сходимости ряда:
, 
, 
.
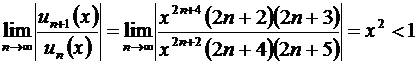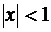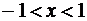Упростим рациональную дробь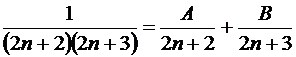 
, 
.
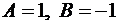Тогда ряд может быть представлен разностью двух рядов:
.
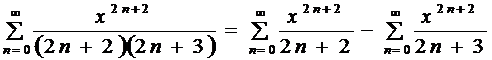Сходимость каждого из них остается та же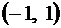 
(убедитесь в этом самостоятельно). Поэтому равенство имеет место. Обозначим суммы рядов соответственно 
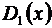и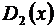 
, а искомую сумму – через 
, 
.
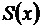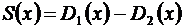Найдем сумму первого ряда:
.
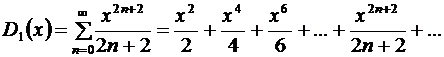Дифференцируя почленно ряд внутри интервала сходимости 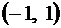, получим: 
; 
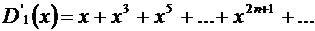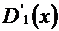представляет собой геометрическую прогрессию со знаменателем 
.
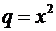При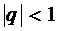 
прогрессия сходится, 
, 
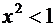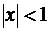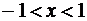, и сумма равна: 
; 
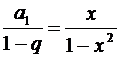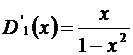. Теперь, интегрируя 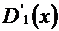на отрезке 
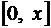, лежащем внутри интервала сходимости 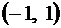, получим:
.
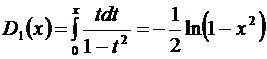Найдем сумму 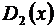второго ряда:
.
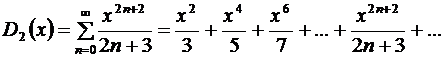Выполним преобразование:
.
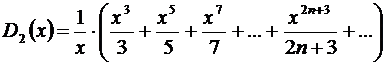Обозначим сумму ряда, стоящего в скобках, через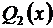 
и продифференцируем 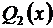в интервале :
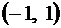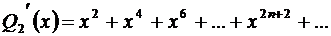– это тоже геометрическая прогрессия.
, , 
;
.
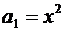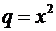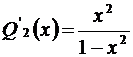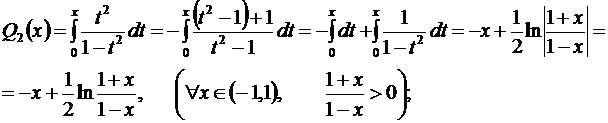
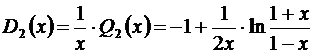Итак, сумма исходного ряда равна:
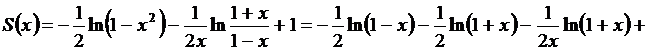
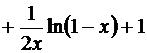или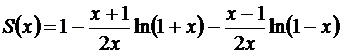 
для .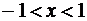
II способ. Не повторяя подробностей I способа, связанных с интервалом сходимости данного ряда, предлагаем II вариант решения задачи. Обозначим сумму ряда через :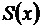 
.
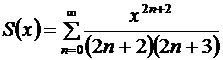Умножим на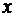 
данный ряд: 
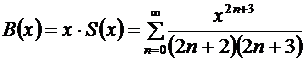. Продифференцируем дважды полученный ряд:
,
.
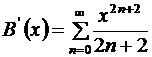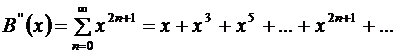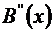представляет собой геометрическую прогрессию со знаменателем 
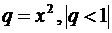, тогда 
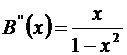. Проинтегрируем 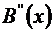на отрезке :
.
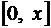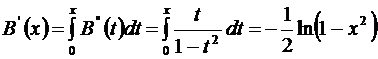Интегрируя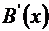 
по частям, получим:
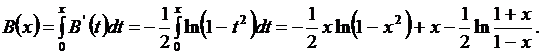
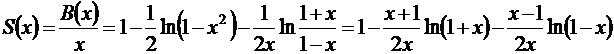
для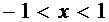 
.
Задача 18.31[7]
Найти сумму ряда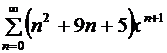 
.
Решение:
Данный ряд сходится в интервале 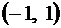(убедитесь в этом самостоятельно). Перепишем его, представив в виде суммы трех рядов:
.
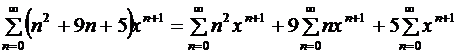Это возможно, так как каждый из рядов имеет одну и ту же область сходимости – интервал 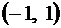. Обозначим суммы трех рядов соответственно через 
, 
, 
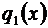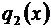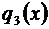, а искомую сумму – через .
.
,
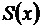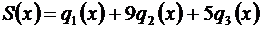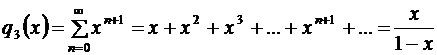как сумма членов геометрической прогрессии со знаменателем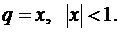 
.
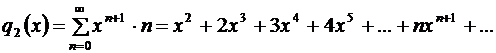Выполним преобразование:
.
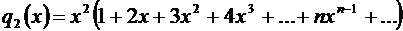Обозначим через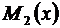 
сумму ряда 
.
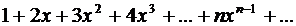Интегрируя почленно этот ряд на отрезке 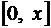внутри интервала сходимости 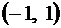, получим:
.
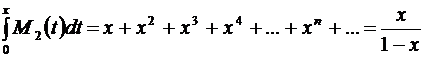Чтобы найти 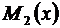, надо продифференцировать дробь 
:
.
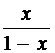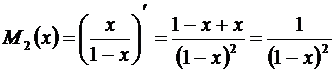Следовательно,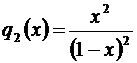 
.
Теперь найдем :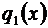
.
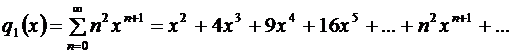Вынесем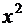 
за скобки:
.
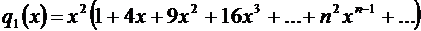Обозначим через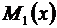 
сумму ряда, стоящего в скобках. Тогда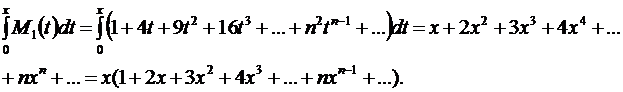 
В этих скобках стоит ряд, сумма которого найдена: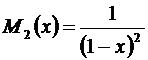 
. Получаем: 
.
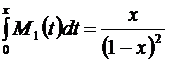Отсюда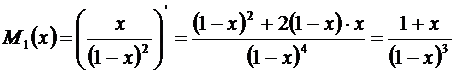 
.
Но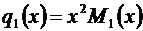 
, 
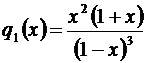. Тогда сумма исходного ряда
.
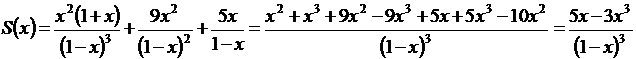Итак,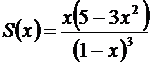 
для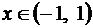 
.
Ряд Тейлора
Определение. Ряд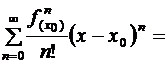 
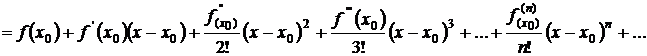
называется рядом Тейлора по степеням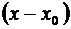 
для функции 
.
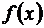Функция 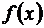может быть разложена в ряд Тейлора, если в рассматриваемой точке 
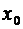она имеет производные всех порядков и если остаточный член в точке 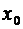при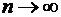 
стремится к нулю. При 
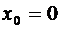ряд Тейлора называют иногда рядом Маклорена.
Теорема
Если функция разлагается в степенной ряд, то для неё этот ряд единственный и является рядом Тейлора.
Примечание. Находя последовательно производные функции 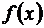и их значения в точке 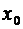, можно записать ряд Тейлора. Но при этом исследование остаточного члена 
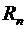представляет большие трудности. Поэтому часто идут другим путем: пользуются готовыми разложениями основных элементарных функций в степенные ряды в комбинациях с правилами сложения, вычитания, умножения рядов и теоремами об их интегрировании и дифференцировании, как это, например, было показано в задачах 17.31 и 18.31.
Задача 19.31[7]
Разложить функцию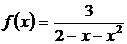 
в ряд Тейлора по степеням .
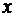Решение:
х0 = 0. Воспользуемся примечанием. Так как
,
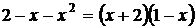то функция упрощается, если применить метод неопределенных коэффициентов:
.
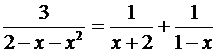Далее раскладываем в ряд каждое слагаемое, пользуясь геометрической прогрессией:
.
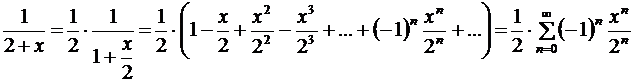Сумма членов геометрической прогрессии со знаменателем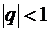 
равна: 
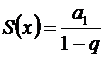. В нашем случае 
. 
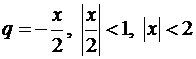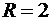– радиус сходимости этого ряда. Слагаемое 
, 
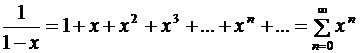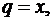
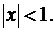
Складывая ряды, получим: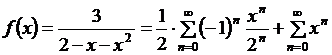 
или 
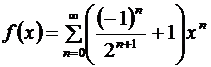, где 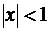– общая область сходимости.
4.1 Приближенное вычисление интегралов с помощью
степенных рядов
Чтобы вычислить интеграл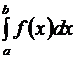 
с заданной точностью, подынтегральную функцию 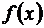раскладывают в ряд, производят интегрирование и в полученном ряде оставляют столько членов, сколько потребуется для заданной точности (см. задачу 9.31).
Задача 20.31[7]
Вычислить интеграл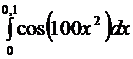 
с точностью до 0,001.
Решение:
Пользуясь разложением функции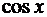 
в ряд Маклорена, заменяя в нем 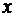на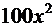 
, имеем:
.
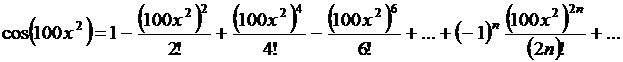Toгдa
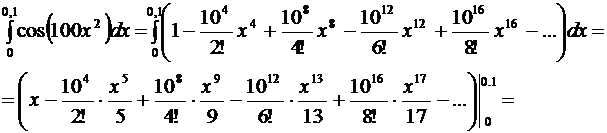
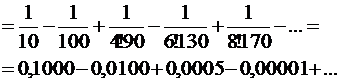
Почленное интегрирование законно, так как отрезок интегрирования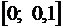 
целиком лежит в области сходимости ряда 
.
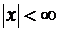Чтобы вычислить данный интеграл с точностью до 0,001, надо взять в полученном ряде два его члена (0,0005<0,001) (см. задачу 9.31).
Таким образом,
.
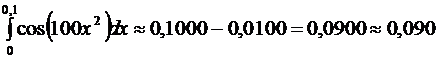Вопросы для самопроверки
Числовые ряды
1. Дайте определения сходящихся и расходящихся рядов.
2. Сформулируйте необходимый признак сходимости ряда.
3. Сформулируйте достаточные признаки сходимости рядов с положительными членами: сравнение рядов с положительными членами; признак Даламбера; радикальный признак Коши, интегральный признак Коши.
4. Дайте определение абсолютно сходящегося ряда. Сформулируйте свойства абсолютно сходящихся рядов.
5. Сформулируйте признак Лейбница.
Функциональные ряды
6. Дайте определение области сходимости функционального ряда.
7. Какой ряд называется равномерно сходящимся?
8. Сформулируйте признак Вейерштрасса.
9. Условия разложимости функции в ряд Тейлора.
10. Сформулируйте теоремы об интегрировании и дифференцировании степенных рядов.
11. Изложите метод приближенного вычисления определенных интегралов с помощью рядов.
Список рекомендуемой литературы
1. Кудрявцев Л.Д. Краткий курс математического анализа. – М.: Наука, 1989. – 736 с.
2. Бугров Я.С. Дифференциальное и интегральное исчисления /Я.С. Бугров, С.М. Никольский. – М.: Наука, 1984. – 432 с.
3. Шмелев П.А. Теория рядов в задачах и упражнениях. – М.: Высшая школа, 1983. – 176 с.
4. Пискунов Н.С. Дифференциальное и интегральное исчисления для втузов. Т. 2. – М.: Наука, 1985. – 576 с.
5. Фихтенгольц Г.М. Курс дифференциального и интегрального исчисления. Т. 2. – М.: Физматгиз, 1962. – 808 с.
6. Запорожец Г.И. Руководство к решению задач по математическому анализу. – М.: Высшая школа, 1966. – 460 с.
7. Кузнецов Л.А. Сборник заданий по высшей математике (ТР). – М.: Высшая школа, 1983. – 174 с.
8. Данко П.Е. Высшая математика в упражнениях и задачах. Ч. 2 /П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова. – М.: Высшая школа, 1986. – 415 с.
9. Бронштейн И.Н. Справочник по математике для инженеров и учащихся втузов / И.Н. Бронштейн, К.А. Семендяев. – М.: Наука, 1986. – 544 с.
Учебное издание
Бородин Николай Павлович
Жернова Варвара Викторовна
Шуметова Людмила Викторовна
Шоркин Владимир Сергеевич
РЯДЫ
Учебно-методическое пособие
Редактор Т.Д. Васильева
Технический редактор Т.П. Прокудина
Орловский государственный технический университет
Лицензия ИД № 00670 от 05.01.2000
Подписано к печати 26.08.2004 г. Формат 60 x 84 1/16.
Печать офсетная. Уч.-изд. л. 1,9. Усл. печ. л. 2,4. Тираж 500 экз.
Заказ №____
Отпечатано с готового оригинал-макета
на полиграфической базе ОрелГТУ,
302030, г. Орел, ул. Московская, 65.